Решающие правила в Задачах принятия решений (ЗПР) в условиях вероятностной неопределенности кратко

Привет, Вы узнаете о том , что такое решающее правило, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое решающее правило , настоятельно рекомендую прочитать все из категории Теория принятия решений.

решающее правило - это метод или модель, позволяющие выбрать решение, наиболее предпочтительное в каком-либо смысле.

Решающее правило называется субъективным, если, основываясь на одной и той же исходной информации, различные исследователи приходят к различным выводам.

Возможны следующие варианты:

1. Модель – объективна, решающее правило – объективно.

2. Модель – объективна, решающее правило – субъективно.

3. Модель – субъективно, решающее правило – объективно.

4. Модель – субъективно, решающее правило – субъективно.

Задачу принятия решений(ЗПР) в условиях неопределенности можно рассматривать как игру против природы. Поэтому и выбор решающего правила можно рассматривать как стратегию, которую выбирает Лицо, принимающее решение (ЛПР) в этой игре. При этом выбрать стратегию, которая бы приводила к минимальному ущербу или максимальному выигрышу в независимости от того, каким окажется состояние природы, невозможно. Одним из способов решения этой проблемы является выбор такого правила, которое бы позволяло определить, насколько стратегия хороша «в среднем». Ранее были определены такие понятия, как мера риска и полезность, которые и дают такие оценки. На их основе и определим следующие решающие правила, позволяющие ЛПР найти наилучшие альтернативы.

1. Экстремальная оптимизация по мере риска. Согласно этому правилу наилучшими считаются альтернативы х* € X, для которых при некоторых заранее определенных ожидаемого значения М и функции потерь ? мера риска минимальна

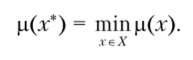
Можно также задать некоторое пороговое значение риска с* е и считать наилучшими такие альтернативы, для которых выполнено условие

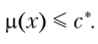
2. Экстремальная оптимизация по полезности. В данном случае наилучшими считаются альтернативы, для которых некоторая заранее заданная функция полезности и достигает своего максимума

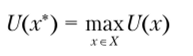
или превосходит некоторое заранее заданное пороговое значение с* е ЧЛ:

Пример определения решающего правила ЗПР в условиях вероятностной неопределенности

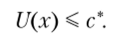
В качестве примера задачи принятия решений в условиях вероятностной неопределенности рассмотрим задачу построения оптимального инвестиционного портфеля.

Пусть имеется п ценных бумаг, характеризуемых своими доходностями. Об этом говорит сайт https://intellect.icu . Доходность 1-й ценной бумаги при вложении в него единичного капитала описывается случайной величиной ξi, i = 1,2, ..., п. Доходности отдельных ценных бумаг в общем случае не являются независимыми случайными величинами. Таким образом, имеется случайный вектор 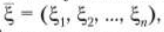характеристики которого определяются состоянием финансового рынка. Каждая конкретная его реализация, т.е. получаемый набор доходностей, и есть реализация состояния окружающей среды.

В данные бумаги инвестируется единица капитала так, что у, — его доля, инвестируемая в г-й вид ценной бумаги. Инвестиционным портфелем у называется набор чисел у₁,у₂,.... у_n удовлетворяющий условию у₁+ у₂ +... + уn = 1. Заметим, что некоторые yi, могут быть нулевыми, что означает, что капитал в данную ценную бумагу не инвестируется, или отрицательными, что означает продажу ценной бумаги без покрытия.

Задача принятия решений в данном случае состоит в том, чтобы построить инвестиционный портфель, т.е. определить, каким образом следует распределить единицу капитала между ценными бумагами. Альтернативами при этом будут конкретные значения портфеля, т.е. конкретные наборы вкладываемых капиталов в имеющиеся ценные бумаги.

Результатом принятия решения по формированию инвестиционного портфеля будет его доходность — случайная величина

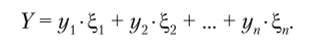
Для решения задачи построения оптимального инвестиционного портфеля необходимо построить решающее правило, определяющее, при каком наборе долей капитала y1 y2,уп, таком, что y1, + у2 + ... уп = 1, результат (доходность портфеля) будет наилучшим. Обозначим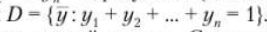

Рассмотрим несколько подходов к решению данной задачи. Сначала рассмотрим экстремальную оптимизацию по полезности.

По определению полезностью доходности портфеля является число

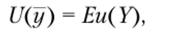
где и — некоторая неубывающая функция. Положим, что и(t) = t для всех вещественных чисел 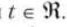. Тогда полезностью будет математическое ожидание доходности портфеля

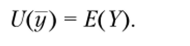
Наиболее предпочтительным будет такой набор долей капитала у * = = {y1*, у2*,..., уn*}, при котором среднее значение доходности портфеля будет максимальным

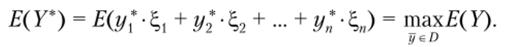
Заметим, что по свойствам математического ожидания

Е(У) = у₁ Е(ξ₁) + у2 Е{ξ ₂ ) + ... + уп-Е( ξ _n).

Таким образом, для построения оптимального инвестиционного портфеля при использовании данного подхода не нужно знать законы распределения доходностей входящих в портфель ценных бумаг. Достаточно оценить только их средние значения. Однако такой подход обладает рядом недостатков, так как оценивает только средние значения и не учитывает возможные отклонения доходностей от них, хотя такие отклонения могут быть достаточно существенны.

Для определения полезности доходности портфеля можно выбирать и другие виды функции и> например, и(t) = 1 - ехр(-at) , где а > 0 — некоторый заданный параметр. Тогда наиболее предпочтительным будет такой портфель 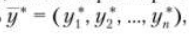, что

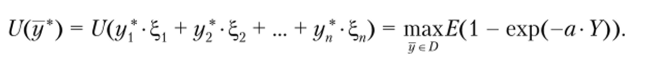
Недостатком данного подхода является сложность его применения. В частности, необходимо определить точный закон распределения вектора доходностей ценных бумаг.

Рассмотрим другой способ построения решающего правила решения задачи нахождения оптимального инвестиционного портфеля — экстремальную оптимизацию по мере риска.

Наиболее распространенной мерой риска является дисперсия случайной величины

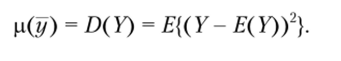
Тогда наиболее предпочтительным будет такой портфель 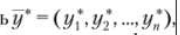при котором среднее отклонение доходности инвестиционного портфеля от своего среднего значения будет минимальным: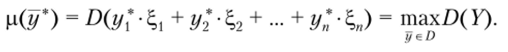

Для нахождения дисперсии доходности портфеля необходимо знать дисперсии доходностей входящих в него ценных бумаг, а также их попарные ковариации, т.е. 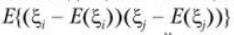для всех . Сами законы распределения доходностей ценных бумаг знать не обязательно. Это упрощает решение данной задачи.

В целом разные подходы к решению могут давать разные и даже противоположные решения. Выбор конкретного способа решения остается за лицом, принимающим решение .

• Выбор именно такой функции полезности обусловлен тем, что для нес функция неприятияриска является константой. Болес подробно с этим можно познакомиться, например, в работе:PrattJ. V. Risk Aversion in the Small and in the Large // Econometrica. 1964. V. 32. P. 122—136.
• Болес подробно с задачей построения оптимального инвестиционного портфеля можнопознакомиться, например, в кн.: Новоселова А. А. Математическое моделирование финансовых рисков. Теория измерения. Новосибирск, 2001.

Вау!! 😲 Ты еще не читал? Это зря!

введение в теорию принятия решений ,

Исследование, описанное в статье про решающее правило, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое решающее правило и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений

Из статьи мы узнали кратко, но содержательно про решающее правило