Лекция
Привет, Вы узнаете о том , что такое Обобщенный критерий и кривые безразличия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Обобщенный критерий и кривые безразличия , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Множество критериев многокритериальной ЗПР, с одной стороны, позволяют характеризовать объект с разных сторон, однако, с другой стороны, создают дополнительную трудность принятия обоснованного решения, так как множество вещественных векторов неупорядоченно. Обобщенным критерием ЗПР является такой критерий, который сводит все оценки по отдельным критериям в единую числовую оценку.
Определение
Обобщенным критерием многокритериальной ЗПР называется критерий, имеющий целевую (критериальную) функцию <р: У —? 9?, ставящую в соответствие каждой векторной оценке ЗПР у = (г/,, у2,..., ут) е У некоторое числовое значение так, что верно следующее соотношение:
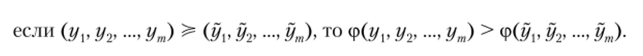
При этом критериальная функция называется функцией полезности (ценности) многокритериальной ЗПР.
Достаточным условием существования обобщенного критерия является условие непрерывности отношения предпочтения. При этом часто используемое на практике отношение лексикографического предпочтения из-за отсутствия непрерывности является непригодным для построения обобщенного критерия.
Обратите внимание!
В практических задачах в качестве отношения предпочтения, по которому строится обобщенный критерий, применяется доминирование по Парето.
Для обобщенного критерия важно не конкретное значение целевой функции, а сравнение этих значений для разных векторных оценок ЗПР.
Поэтому критерии будут разбиваться на классы эквивалентных критериев.
Определение
Обобщенные критерии с функциями полезности ф, и ф2 называются эквивалентными, если для любых векторных оценок у = (г/,, г/2,ут) и у = (у{, у2,..., ут) выполнено следующее соотношение:
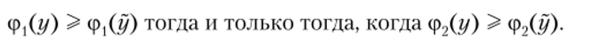
Пример эквивалентных функций полезности. Предположим, что для двухкритериальной ЗПР обобщенный критерий с функцией полезности имеет вид ф(г/,, у2) = ух + 2уТ Тогда обобщенные критерии с функциями полезности ф{(ух, у2) = 3ух + 6у2 и ф2(ух, у2) = еу'+2у2 будут ему эквивалентны.
Вообще говоря, любой обобщенный критерий с функцией полезности вида Т = й'о ф, где# — произвольная неубывающая функция, будет эквивалентен обобщенному критерию с функцией полезности ф (здесь знак ° означает композицию функций). Об этом говорит сайт https://intellect.icu . В частности критерии вида Т = ахр, где а — константа, эквиваленты ф.
Поскольку критериальная функция интерпретируется как функция полезности многокритериальной ЗПР, дальнейшее развитие теории будет происходить в соответствии с ординалистским (порядковым) подходом, разработанным В. Парето , который предложил рассматривать не саму полезность товаров или наборов, а выводимую эмпирическим путем оценку предпочтений одних товаров по отношению к другим. Основным инструментом анализа в таких задачах стали кривые безразличия, предложенные Ф. Эджвортом.
Предположим для простоты, что имеются только два критерия с оценками у] е У, и у2 е У2 соответственно.
Определение
Кривой безразличия называются такие комбинации значений критериев ух е У, и у2 е У2, которые удовлетворяют уравнению ф(г/,, у2) = с, где ф — некоторая построенная функция полезности, а с — заданная константа.
Рассмотрим две равнозначные, т.е. лежащие на одной и той же кривой безразличия, точки А(у{> у2) и В(у[, у2) и обозначим Дг/, = у[ - г/,, Ау2 = у2 - у2. При переходе от точки А к точке В за улучшение значения ух на | Дг/11 ЛГ1Р готово «заплатить» ухудшением значения у2 на | Ау2 (рис. 8.2).
Обратите внимание!
Для точек, лежащих на одной кривой безразличия, величины ух и у2 всегда имеют разные знаки.
Положительное число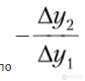 
будет зависеть от обеих точек А и В. Для
того чтобы исключить зависимость от точки В, рассмотрим бесконечно малое смещение.
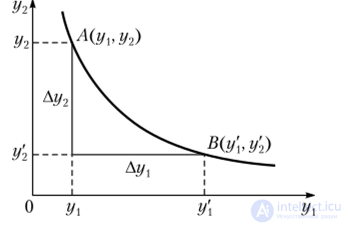
Рис. 8.2. Движение точки на кривой безразличия
Определение
Локальным коэффициентом замещения (Л КЗ) в точке Л(г/,, у2) называется положительное число
если такой предел существует и конечен.
Обратите внимание!
Локальный коэффициент замещения X зависит от координат точки А, т.е. X = = Х(уру2).
Строго говоря, ЛКЗ можно найти следующим образом. Поскольку кривая безразличия задается уравнением <р(г/,, у2) = с, где с — константа, в случае, когда функция (р(г/,, у2) — непрерывно дифференцируема, это уравнение можно переписать следующим образом
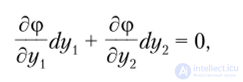
где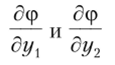 
— частные производные по ух и у2 соответственно. Тогда
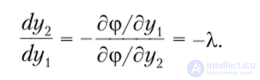
На рис. 8.3 показан геометрический смысл ЛКЗ: ЛКЗ в точке А(у1, у2) равен взятому со знаком минус тангенсу угла наклона к оси 0у2 касательной, проведенной к кривой безразличия в точке А(у{, у2).
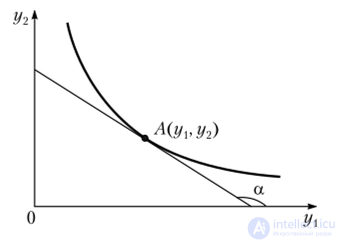
Рис. 83. Геометрический смысл ЛКЗ: X = -tg(x
Кривую безразличия можно построить для каждого значения критериальной функции. Кроме того из определения следует, что через любую точку А(у 1, у2) проходит единственная кривая безразличия. Таким образом, для ЗГ1Р имеем множество таких кривых.
Определение
Множество кривых безразличия некоторой двухкритериальной ЗПР называется картой безразличия.
На рис. 8.4 показана карта безразличия ЗПР с множеством векторных оценок У.
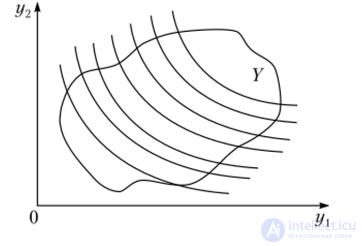
Рис.. 8.4. Карта безразличия
Обратите внимание!
В случае, когда кривые безразличия являются гладкими функциями, т.е. имеющими производные в каждой точке, задание карты безразличия ЗПР равносильно заданию для каждой точки А е У ее ЛКЗ.
Действительно, если задана карта безразличия, то для каждой точки А е У существует единственная проходящая через нее кривая безразличия. Проведя в этой точке касательную к кривой, найдем тангенс угла наклона этой касательной к оси абсцисс. Это и будет ЛКЗ (см. рис. 8.3).
Обратно, если для каждой точки А(у{, у2) е У задан соответствующий ЛКЗ, то это означает, что в каждой точке задан тангенс угла наклона касательной к кривой безразличия. В этом случае можно построить и саму кривую.
Исследование, описанное в статье про Обобщенный критерий и кривые безразличия, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Обобщенный критерий и кривые безразличия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений