Аддитивные функции полезности кратко

Привет, Вы узнаете о том , что такое Аддитивные функции полезности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Аддитивные функции полезности , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Построение функции полезности (ценности) обобщенного критерия существенно упрощается, если эта функция аддитивна.

Определение

Функция полезности ср(г/,, уТ ..., ут) обобщенного критерия двухкритериальной ЗПР называется аддитивной, если ее можно представить в виде

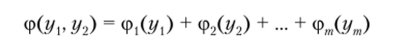
с функциями

Класс аддитивных функций достаточно велик. В частности, если функция полезности имеет вид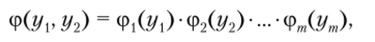

то, поскольку можно применить произвольное монотонное преобразование и получить при этом эквивалентный критерий, прологарифмируем описанную функцию ср. Тогда получим тоже аддитивную функцию

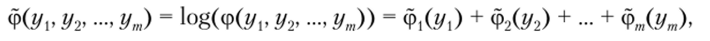
где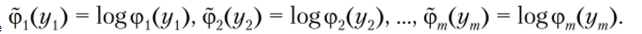

Опишем необходимые и достаточные условия существования аддитивной функции полезности в случае двух критериев. Пусть функция полезности аддитивна. Тогда для произвольной точки А(у{, у2) е У справедливо представление

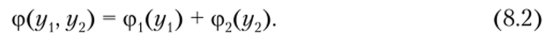
Рассмотрим четыре точки: 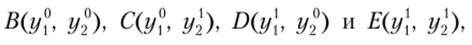для которых определены ЛКЗ (рис. 8.5).

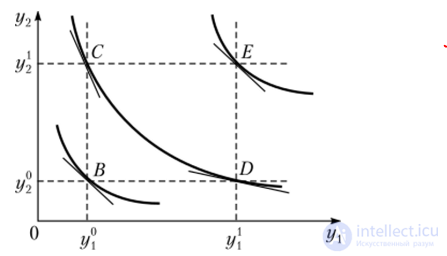
Рис. 85. Условия существования аддитивной функции полезности

Локальный коэффициент замещения в точке Е будет рассчитываться как

где ф', и фз — производные функций ф, и ф2 соответственно. Об этом говорит сайт https://intellect.icu . Тогда можно записать следующее соотношение

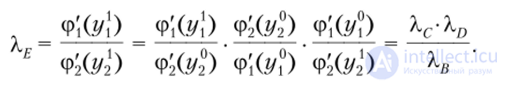
Следовательно, необходимым условием существования аддитивной функции полезности является условие соответственных замещений

где Хв, Ха Хп — ЛКЗ в точках В, С и О соответственно.

Можно доказать, что это условие является достаточным.

Процедура построения кривых безразличия в случае аддитивной функции полезности вида (8.2) проще, чем в общем случае.

Как уже упоминалось в параграфе 8.4, функция полезности не является однозначно определенной. Поэтому сначала необходимо задать начало отсчета, т.е. указать множество точек нулевой полезности, и единицы измерения для строящихся кривых безразличия. Для этого ЛПР необходимо указать минимальные допустимые значения критериев у и у®, для которых положим

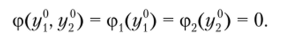
Затем необходимо выбрать точку у > г/®, для которой положить (р,(г/{) = 1, задав тем самым масштаб измерения.

Далее ЛИР необходимо указать значение у] > г/® Для второго критерия такое, чтобы пары (у, г/®) и (у, У2) были одинаково предпочтительны, т.е. Ф (у, у) = ф(/у,, у',). Для этого значения положим ср2(г/ 2) = 1. ЛПР также необходимо указать такие значения у > у и у > у для первого и второго критериев соответственно, чтобы пары (у, г/2°), (у, у.] ) и (у, у1) были одинаково предпочтительны или равноценны для ЛПР. Затем положим ср,(г/7) = = ф2(г/2) = 2, что действительно можно сделать, поскольку верны следующие соотношения

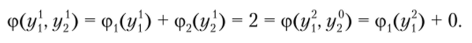
Аналогично

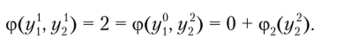
Соединяя равноценные точки, получим аппроксимацию кривой безразличия.

Далее поиск новых значений продолжается аналогичным образом, т.е. выбираются у] > у и у > у1 для первого и второго критериев соответственно, что пары (г/,, г/®), (у{, г/2), (у, у2) и (г/®, у) одинаково предпочтительны или равноценны для ЛПР. Выбрав такие значения, полагаем ф,(г/?) = ф2(у2!) = 3- Соединяя равноценные точки, получим аппроксимацию следующей кривой безразличия. Построение остальных кривых осуществляется аналогичным образом (рис 8.6).

Как видно из построения, рассмотренная процедура предъявляет достаточно высокие требования к «чувствительности» ЛПР — неопределенные ответы ЛПР по поводу предпочтительности тех или иных значений критериев недопустимы. При этом сравнение критериальных точек осуществляется многократно. Для того чтобы исключить противоречивость ответов ЛПР на вопросы о предпочтительности точек, необходимо во время проведения процедуры построения кривых безразличия и функции полезности проверять условие (8.3). Заметим также, что при увеличении числа критериев сложность задачи построения функции полезности увеличивается многократно.

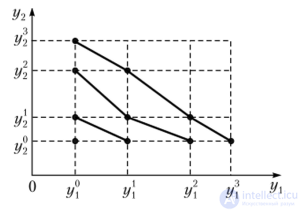
Рис. 8.6. Построение кривых безразличия

Поскольку описанная процедура построения функции полезности сложна в применении, на практике чаще используют альтернативные методы, которые будут описаны ниже в других главах.

Исследование, описанное в статье про Аддитивные функции полезности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Аддитивные функции полезности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.