Построение и аппроксимация множества Парето - Эджворта

Привет, Вы узнаете о том , что такое Построение и аппроксимация множества Парето - Эджворта, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Построение и аппроксимация множества Парето - Эджворта , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Аналитические методы при наличии нелинейных критериев и зависимостей также оказываются чересчур сложными и недостаточно эффективными, поэтому практика показывает превосходство численных процедур.

Обратите внимание!

Для трех и более критериев множество Парето — Эджворта лучше строить, применяя компьютерные программы и алгоритмы.

В случае конечного дискретного множества альтернатив X, состоящего из п элементов, задача сводится к попарному сравнению альтернатив. Общее число пар равно 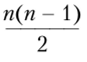, в каждой паре нужно провести т сравнений

по всем т критериям. Подобные задачи реализуются во многих прикладных программных пакетах, зачастую — в виде встроенных функций. На практике числа альтернатив п и критериев т обычно невелики, и в таких случаях время расчета на современных компьютерах можно считать пренебрежимо малым.

Однако для множества альтернатив X в виде области складывается принципиально иная ситуация. Если нет дополнительных предположений о виде множества Парето — Эджворта (например, о его выпуклости), то вычислительная сложность алгоритма его нахождения может быть очень высокой.

Простейший из таких алгоритмов — сеточный метод , основанный на сведении непрерывного случая к дискретному. Для этого исходная область X покрывается мелкой сеткой с узлами в точкахХ., г = 1,..., N, и затем во всех N узлах вычисляются векторные оценки у. =/(*?). При этом число N быстро возрастает с увеличением размерности исходной области X и может достигать очень больших значений. Среди оценок г/,, составляющих конечный набор точек в критериальном пространстве, методами парных сравнений выбираются недоминируемые векторы у*, образующие дискретную аппроксимацию множества Парето — Эджворта в критериальном пространстве (или фронт Парето). Соответствующие оценкам у*уточки исходной области X (иначе говоря, прообразы величин г/Д т.е. у* = представляют

собой дискретную аппроксимацию множества Парето — Эджворта. Для непрерывной аппроксимации (не только в узлах, но и между ними) фронта Парето, представляющего собой поверхность в га-мерном пространстве используется многогранник PN (определяемый числом N узлов), т.е. совокупность участков гиперплоскостей в проходящих через узлы сетки.

Как показывает практика, сеточный метод может требовать неприемлемо высоких вычислительных ресурсов. Действительно, нередки следующие два вида ситуаций.

• • Если требуется высокая точность г аппроксимации множеств Парето по т критериям, JV имеет порядок г В таких случаях число N узлов сетки может оказаться чрезвычайно большим. Например, при в = 0,001 и т = 10 имеем N ~ Ю30 — объем вычислений, превосходящий возможности самых мощных компьютеров.
• • Когда сложно вычисляются целевые функции, причем эти сложные вычисления требуется повторить N раз, суммарное время расчетов и требуемые ресурсы также велики.

Поэтому в настоящее время интенсивно развиваются альтернативные методы, основанные на более «умных» алгоритмах, экономящих вычислительные ресурсы путем учета результатов уже произведенных вычислений для оптимизации последующих процедур.

Класс «наивных» методов, выделяемый Люком (S. Luke), основан на лексикографической турнирной селекции (lexicographic tournament selection ) и исходит из того, что частные критерии упорядочены но важности, так что самым важным является, к примеру, критерий следующим по важности — критерий f2(x) и т.д. Сама по себе идея турнирной селекции широко распространена в практических расчетах благодаря своей простоте. Вместо полного набора сравнений каждого из N вариантов с каждым производится случайная выборка t альтернатив — формируется турнир из t претендентов, внутри которого осуществляется попарное сопоставление всех альтернатив. По результатам турнира отбрасываются все доминируемые точки, а также все «худшие»: для этого определяется «фитнес»-функция (т.е. функция пригодности, сходная с целевой функцией), по значениям которой оцениваются возможности двух противоположных исходов — либо альтернатива окажется доминируемой, либо войдет в множество Парето — Эджворта. Турниры повторяются много раз, пока не будет охвачено практически все множество альтернатив. Общее количество операций сравнения (т.е. и объем вычислений) значительно сокращается, поскольку относительно небольшое количество 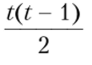сравнений позволяет в каждом турнире отсеивать постоянную долю альтернатив. Однако «наивные» методы работают не всегда и часто мало эффективны. На практике оказывается непросто подобрать как «фитнес»-функцию, так и величину турнира ?. При малых значениях Ь велика вероятность ошибки — отбрасывания точек множества Парето — Эджворта из-за случайного попадания «сильных соперников» в один турнир. При больших ?, сопоставимых с ЛГ, объем вычислений снижается недостаточно быстро из-за роста числа «лишних» сопоставлений.

Чтобы уменьшить число сравнений (а тем самым — и вычислительные затраты), разработаны адаптивные алгоритмы, вычислительные схемы которых приспосабливаются (адаптируются) к ситуации, т.е. меняют свои параметры в разных местах расчетной области . Адаптивные алгоритмы относятся к классу итерационных, т.е. к классу методов последовательных приближений. Выбирается некоторое начальное приближение — например, путем построения крупной сетки с небольшим числом узлов, расчет которой не составляет труда, так как число узлов N невелико. В дальнейшем каждое следующее приближение строится с учетом информации, полученной на предыдущих шагах. Адаптивные численные схемы отличаются тем, что процедура построения следующего приближения по найденному предыдущему не фиксирована, т.е. зависит от результатов уже выполненного расчета. Главное преимущество адаптивных алгоритмов состоит в возможности экономии ресурсов и расчетного времени за счет более интенсивного поиска в «перспективных» участках (с более высокими величинами частных критериев) и менее интенсивного поиска среди «аутсайдеров».

Для анализа точности адаптивных методов применяются «эталонные» многогранники Рдг, на которых достигается минимум расстояния по Хаус- дорфу 8(РдГ, Ру) между фронтом Парето Ру и многогранником Рх. Эти многогранники называются многогранниками наилучшей аппроксимации. Об этом говорит сайт https://intellect.icu . Они могут служить образцом аппроксимации образа Ру множества Парето — Эджворта. Хотя существование таких многогранников доказано теоретически, но практические методы построения многогранников наилучшей аппроксимации отсутствуют. Однако их свойства известны, поэтому они полезны для изучения качества численных методов аппроксимации. В частности, известна асимптотическая оценка порядка величины расстояния по Хаусдорфу при возрастании числа N узлов: 8 {PN, PY) ~ const • N 1(т 1) при N

Обратите внимание!

Смысл асимптотической оценки для практических приложений состоит прежде всего в том, что она показывает резкое падение точности аппроксимации 5(РЛ, Ру) с ростом числа т критериев.

Если при т = 2 и т = 3 погрешность составляет соответственно N 1 и ЛГ , т.е. точность 1% достигается для N = 10 (при т = 2) и N = 100 (при т = 3), то при т = 9 погрешность уже имеет порядок ЛС0’Ь, что составит 1% только для N = 108. При этом нужно учесть, что приведенные оценки — лишь погрешности наилучшей аппроксимации, т.е. реальные расчетные приближения могут оказаться значительно менее точными.

Обратите внимание!

Теоретически обоснованная неточность аппроксимации 8(РУ, Ру) требует использования более точных методов с ростом числа т критериев.

Один из относительно новых и высокоэффективных классов адаптивных алгоритмов построения множества Парето — Эджворта представляют собой генетические алгоритмы. В генетических алгоритмах проведена аналогия между доминированием по Парето и процессом естественного отбора (селекции) в процессе эволюции, когда выживают только сильнейшие, а слабейшие особи погибают.

Среди генетических алгоритмов в вычислительной практике наиболее часто используются четыре метода :

• • метод VEGA {Vector Evaluated Genetic Algorithm)]
• • метод EEG A {Fonseca and Fleming's Multiohjective Genetic Algorithm)]
• • метод NPGA {Niched Pareto Genetic Algorithm)]
• • метод SPEA {Strength Pareto Evolutionary Algorithm).

Общей для всех генетических алгоритмов является ассоциация точек множества X с индивидами популяции, количество которых N при детальной аппроксимации области X с заданной погрешностью ? в пространстве альтернатив Rk имеет порядок N ~ г к. Как и для сеточных методов, N может быть очень велико: уже для к = 6 и ? = 10 2 получим N ~ 1012, т.е. триллион точек. При непосредственном сравнении каждого «индивида» с каждым потребовалось бы порядка N{N - 1)/2 ~ 102i операций. Названные четыре генетических алгоритма обеспечивают гораздо более эффективный отбор и отличаются порядком действий для отсева «слабейших».

В методе VEGA селекция производится по «переключающимся» частным критериям оптимальности, т.е. поочередно производится отсев (путем сопоставления с доминирующими) наиболее слабых «особей» но каждому из частных критериев. Перебрав все частные критерии yv yv ..., ут, возвращаемся снова к первому критерию г/, и т.д. Процесс продолжается но кругу до тех пор, пока не остаются только сильнейшие, не отсеивающиеся «индивиды».

В методе РРСА при моделировании естественного отбора используется процедура турнирной селекции, т.е. организуется «турнир» между «индивидами», в процессе которого вычисляется ранг каждого «индивида» как число частных критериев, по которым он уступил «соперникам». Проигравшие «сопернику» по всем показателям из турнира выбывают, т.е. исключаются из множества Парето — Эджворта. Отбор оптимизируется на основе расчета рангов так, чтобы как можно скорее исключить всех «слабейших».

Метод №СА основан на формировании «популяционных ниш» — на отборе не слабейших, а, напротив, сильнейших (т.е. заведомо не доминируемых) по отдельным частным критериям «особей».

Метод SPEA является самым эффективным, но в то же время самым сложным из числа рассматриваемых методов: он комбинирует селекцию, основанную на Парето-доминировании (как в методе РРСА) с использованием популяционных ниш (МРСА).

Несмотря на важные преимущества, адаптивные алгоритмы обладают также некоторыми недостатками, среди которых отметим следующие.

• • Во-первых, итеративное построение аппроксимации неудобно при использовании параллельных вычислений на нескольких компьютерах, поскольку число решаемых задач оптимизации может резко меняться от итерации к итерации.
• • Во-вторых, практические расчеты показывают, что удобнее всего выполнять построение аппроксимации на специальном ресурсе, а расчет векторного критерия /(х) — на компьютере пользователя; и в этой ситуации наличие итераций приводит к требованию многократного (до нескольких сотен раз) взаимодействия пользователя с ресурсом, что не является практичным, особенно если связь осуществляется через сеть Интернет.

Существует еще ряд вычислительных алгоритмов построения множества Парето —Эджворта различной степени сложности и эффективности, в частности — сигма-метод, методы композитных точек, гиперкубов, динамических соседей, а также метод «хищник —жертва»[11].

Обратите внимание!

Выбор численного метода построения множества Парето — Эджворта определяется сложностью и особенностями многокритериальной задачи, спецификой предпочтений ЛИР, а также наличием соответствующего программного обеспечения и подходящей вычислительной техники для реализации алгоритмов.

Критерии оценки качества Парето-аппроксимации основаны на следующих основных требованиях к методам Парето-аппроксимации:

• • точки найденной аппроксимации должны быть расположены достаточно близко к точному фронту Парето в критериальном пространстве;
• • аппроксимация должна покрывать весь фронт Парето;

• распределению точек аппроксимации следует быть ближе к равномерному распределению в критериальном пространстве.

В современных методах Парето-аппроксимации для выполнения последнего требования используют специальные механизмы, обеспечивающие приемлемый разброс (spread) точек аппроксимации. Наиболее известный механизм такого сорта — механизм нишевания (niching)'. Для оценки равномерности покрытия может быть использована величина, называемая разреженностью (scarcity), имеющая смысл минимального расстояния между решениями, принадлежащими Парето-аппроксимации. Указанное расстояние может быть измерено с помощью различных метрик, например, с помощью известного манхеттеновского расстояния (Manhattan distance).

Примеры расчетов аппроксимации фронта Парето с визуализацией результатов, выполненных в ВЦ РАН им. А. А. Дородницына для конкретных практических задач, можно найти в работах, выполненных под руководством А. В. Лотова[12] [13]. В них представлены результаты по следующим проблемам.

• • Совместная российско-финско-эстонская программа поддержки инвестиций, направляемых на уменьшение выбросов загрязнителей на тех объектах, которые оказывают влияние на состояние атмосферы в Финляндии. Оптимизация проводилась по шести критериям: затратам на уменьшение эмиссии (загрязнения) в каждом из регионов и удельному (на единицу площади) выпадению кислотных осадков в каждом из регионов.
• • Поиск эффективных стратегий улучшения качества воды в реке Ока. Рассматривалось шесть наиболее важных загрязнителей: взвешенные вещества, фосфаты; нитраты; нефтепродукты; соединения железа; биологическое потребление кислорода. В числе критериев — общая стоимость проекта, затраты в отдельных регионах, концентрации загрязняющих веществ по гидрологическим пунктам, расположенным в отдельных регионах, и максимальные концентрации веществ по всей реке.
• • Интегральное планирование принятия решений по бассейну реки Werra (Германия).
• • Оптимизация финансовых вложений в различные российские банки в различных валютах.
• • Оптимизация охлаждения стали водяными струями в металлургическом производстве с учетом многофазности системы и влияния излучения. В качестве критериев были выбраны значения температуры поверхности п градиента температуры в нескольких точках.
• • Формирование диспетчерского графика управления расходом воды для каскада водохранилищ на реке Ангара. Задача состояла в выборе значений 132 параметров, которыми описывался диспетчерский график (по шесть параметров кривой расхода для каждого периода при 22 периодах, на которые был разбит год). Требовалось минимизировать восемь критериев, представлявших собой различные штрафы (за наличие холостого сброса, за нарушение минимальных уровней водосброса в различные периоды, за превышение уровня водосброса, за понижение уровня отдаваемой мощности и т.п.). Полученные в результате расчета графики значений шести рассмотренных параметров в зависимости от времени в одной из найденных точек множества Парето — Эджворта представлены для иллюстрации на рис. 9.6 (визуализация фронта Парето затруднительна из-за высокой размерности критериального пространства т = 8). По оси абсцисс отложено время (год, разбитый на 22 периода), а по оси ординат — значения всех шести параметров расхода, которые регулируются диспетчерами на плотинах гидроэлектростанций, формирующих каскад водохранилищ на реке Ангара (детальная информация об этих шести технических параметрах чересчур обширна, ее можно найти в описании результатов расчета).

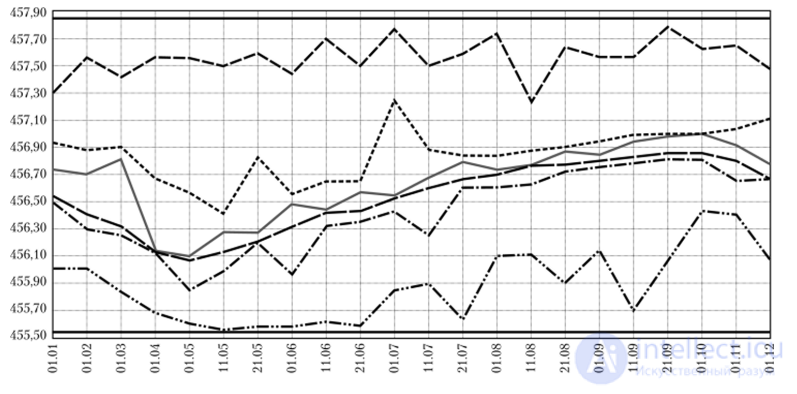
Рис. 9.6. Графики шести рассмотренных параметров по всем 22 периодам года в одной из найденных целевых точек множества Парето —Эджворта, отвечающей значениям восьми критериев ух = 0,86, у2 = уъ = уА = у6 = у1 = 0, у5 = 0,77, ун = 0,93, в задаче о каскаде водохранилищ

Графики иллюстрируют не фронт в критериальном пространстве, а именно множество Парето — Эджворта в пространстве альтернатив. Представленные на рис. 9.6 результаты демонстрируют гот факт, что оптимальные решения нередко не являются гладкими функциями и могут иметь заметные изломы и перепады.

В целом анализ практических приложений компьютерного моделирования фронта Парето позволяет дать следующие рекомендации.

Обратите внимание!

Для построения и аппроксимации множества Парето — Эджворта при наличии трех и более критериев целесообразно применение компьютерного моделирования и численных алгоритмов (сеточных, «наивных», адаптивных и др.). При этом даже теоретически наилучшая из возможных аппроксимаций фронта Парето имеет существенную погрешность, асимптотическая оценка которой по N узлам сетки (6(РЛ., Ру) ~ сош^У 2/(;”_,) при N —»? °°) резко возрастает с увеличением числа т критериев. Поэтому для приближения целесообразно использовать наиболее точные и эффективные численные алгоритмы, к которым относятся четыре вида генетических алгоритмов, включая методы VEGA (Vector Evaluated Genetic Algorithm), EEGA (Fonseca and Fleming’s Multiobjective Genetic Algorithm), NPGA (Niched Pareto Genetic Algorithm) и SPEA (Strength Pareto Evolutionary Algorithm).

Комбинирование численных методов с геометрической интерпретацией и визуализацией множества Парето — Эджворта обеспечивает ЛПР наилучшими возможностями для принятия решений.

• Ларичев О. И. Теория и методы принятия решений : учебник для вузов. М.: Университетская книга, Логос, 2006. 392 с.
• Luke S. Essentials of Metaheuristics. A Set of Undergraduate Lecture Notes [Электронныйресурс]. Department of Computer Science George Mason University, Online Version 2.0. June,2013. 253 p. URL: http://cs.gmu.edu/~scan/book/metaheuristics/Esscntials.pdf (дата обращения: 04.08.2015).
• Eichfehler G. Adaptive Scalarization Methods in Multiobjective Optimization. Springer, 2008.256 p.
• Каменев Г. К. Оптимальные адаптивные методы полиэдральной аппроксимации выпуклых тел. М.: Изд-во ВЦ РАН, 2007. 233 с.
• Карпенко А. П., Овчинников В. А., Семенихин А. С. Распределенная программная система
• для построения множества Парето в задаче многокритериальной оптимизации динамических
• систем с использованием параллельного генетического алгоритма [Электронный ресурс] //
• Наука и образование. 2008. № 7.1ШЬ: http://technomag.bmstu.ru/doc/98973.html (дата обра
• щения: 04.08.2015).
• [10] Карпенко А. П., Овчинников В. А., Семенихин А. С. Распределенная программная система
• [11] Карпенко А. //., Семенихин А. С., Митина Е. В. Популяционные методы аппроксимациимножества Парето в задаче многокритериальной оптимизации [Электронный ресурс] // Наука и образование. 2012. №4. 1ШЬ: http://technomag.cdu.ru/file/out/505243 (дата обращения: 04.08.2015).
• [12] Konak A., Coit D. W., Smith А. Е. Multi-Objective Optimization Using Genetic Algorithms[Электронный ресурс] // IE Working Paper 05-008. Rutgers State University of New Jersey, 2005.P. 24. URL: http://webcache.googleusercontcnt.com/search?q=cachc:DnfDoylaSlQ):neuro.bstu.bv/ai/To-dom/My_research/Papers-0/For-courses/MOGA/paper%25252005-008%255Bl%255D.pdf+&cd=4&hl=ru&ct=clnk&gl=ni (дата обращения: 04.08.2015).
• [13] Group on Visualization-based MCDM techniques (Animated and interactive decision maps,feasible goals method, reasonable goals method) | Электронный ресурс]. URL: http://www.ccas.ru/mmes/mmeda/mcdm.htm (дата обращения: 04.08.2015)

Исследование, описанное в статье про Построение и аппроксимация множества Парето - Эджворта, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Построение и аппроксимация множества Парето - Эджворта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений