Принятие решения в условиях неопределенности. кратко

Привет, Вы узнаете о том , что такое принятие решений в условиях неопределенности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое принятие решений в условиях неопределенности , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Лицо, принимающее решение, имеет информацию стохастического («модельного» в терминах вероятностных моделей) характера о поведении среды. В данном контексте возможны следующие варианты описания состояния среды:

• 1) случайное состояние среды описывается вероятностным пространством (5, 3, Р). Это так называемая классическая «вероятностная тройка». Здесь 3 — а-алгебра событий, т.е. множество случайных событий с системой замкнутой относительно взятия дополнения, счетных объединений и пересечений. Таким образом это позволяет нам рассматривать, как «точечные» состояния среды, так и «множественные». На событиях из а-алге- бры 3 предполагается заданной вероятность (вероятностная мера) Р;
• 2) распределение вероятностей на множестве состояний среды 5 неизвестно, но его можно оценить статистически или посредством эксперимента (так называемый байесовский подход);
• 3) известно множество состояний среды 5, но нет никакой информации об этом множестве, дающей возможность оценить вероятностные свойства этого множества. Задачи такого типа называются задачами принятия решений в условиях полной неопределенности. В данной ситуации формулируется некоторая гипотеза о поведении среды, на основании этой гипотезы строится вероятностное пространство и применяется минимаксный (или максиминный) подход. В том случае, когда множество состояний среды 5 конечно, а вероятность на 5 так или иначе требуется ввести, то обычно каждому элементу из ? присваивается одинаковая вероятность;
• 4) случайность среды определяется целенаправленными действиями контрагентов. В таком случае говорят о принятии решения в теоретико-игровых условиях. Состояние среды здесь меняется в зависимости от информации о действиях контрагента. Типичный пример, когда один контрагент скупает актив, а его оппонент решает вопрос: скупка идет, чтобы поднять цену с целью дальнейшей продажи (игра на повышение), или же от реального спроса.

Задача принятия решений в условиях неопределенности – это задача выбора оптимальной стратегии, исход которой помимо стратегий оперирующей стороны и ряда фиксированных факторов (детерминированных и стохастических) зависит от неопределенных факторов, неподвластных оперирующей стороне и неизвестных ей в момент принятия решений.

Вследствие влияния неопределенных факторов каждой конкретной стратегии (решению) соответствует не единственный исход, а множество исходов. Конкретная реализация исхода для каждого решения определяется конкретной реализацией неопределенных факторов.

Рассмотрим различие между фиксированными стохастическими факторами и неопределенными факторами. И те, и другие факторы приводят к разбросу в возможных исходах при многократной реализации одного и того же решения. В этом их сходство между собой и отличие от детерминированных факторов. Различие же в том, что относительно фиксированных стохастических факторов ЛПР располагает всей полнотой статистической информации – этой информации достаточно для определения вероятностей появлений возможных исходов и принятия решения о выборе оптимального «в среднем» решения. Относительно неопределенных факторов ЛПР такой информацией не располагает.

В дальнейшем будем рассматривать ЗПР в условиях неопределенности без учета фиксированных стохастических факторов.

В отношении вероятностей реализации различных исходов возможны два случая (рис. 4.1):

вероятности возможных исходов не имеют физического смысла – тогда мы имеем дело с неопределенными факторами нестохастической природы;

вероятности возможных исходов имеют физический смысл, но либо неизвестны ЛПР, либо известны с недостаточной для принятия решения точностью – тогда мы имеем дело с неопределенными факторами стохастической природы.

Неопределенные факторы нестохастической природы можно разбить на две группы.

Первую группу составляют факторы стратегической неопределенности – неопределенные факторы, которые появляются за счет участия в операции нескольких оперирующих сторон. Об этом говорит сайт https://intellect.icu . Каждая из сторон вынуждена принимать решения в условиях, когда ей неизвестны будущие действия других участников операции.

Вторую группу составляют факторы концептуальной неопределенности – неопределенные факторы, сопутствующие принятию особо сложных решений, имеющих долговременные или далеко идущие последствия. В этом случае возможно наличие нечетких, неформализованных целей (это относится, к сожалению, к ряду экономических задач).

Задачи принятия решений в условиях стратегической неопределенности (или в условиях конфликтной ситуации) можно подразделить наодноуровневые и многоуровневые.

В одноуровневых задачах принятия решений участники не связаны никакими формами подчинения, они участвуют в одной операции и заинтересованы в том или ином ее исходе.

Многоуровневые задачи принятия решений возникают в сложных системах управления и имеют иерархическую структуру.

Одноуровневые конфликтные ЗПР могут быть антагонистическими и неантагонистическими. В антагонистических сталкиваются интересы двух сторон, преследующих прямо противоположные цели.

К неопределенным факторам стохастической природы относятся природные неопределенности.

Природные неопределенности – неопределенные факторы, появляющиеся из-за недостаточной изученности «природы».

В ТПР под термином «природа» понимают всю совокупность обстоятельств, в условиях которых приходится принимать решение. Это могут быть неизвестные характеристики процессов, связанных с протеканием операции или внешними условиями выполнения операции.

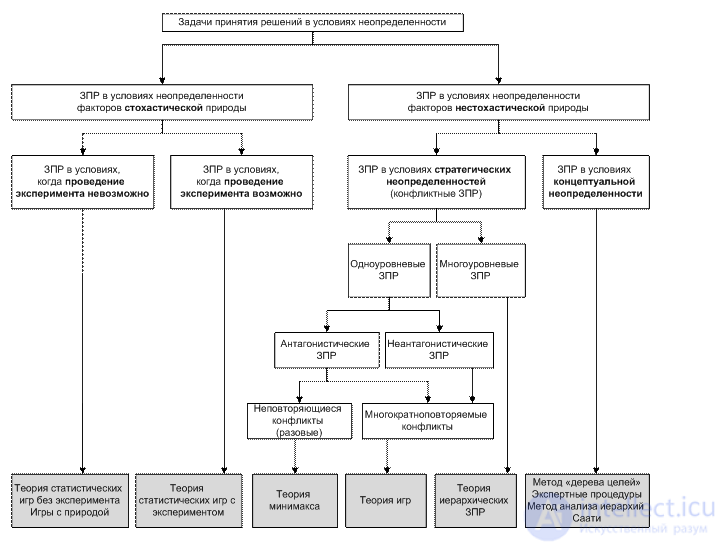
Рис. 4.1. Классификация ЗПР в условиях неопределенности

На рисунке 4.1 представлено «дерево» задач принятия решений в условиях неопределенности. «Листочки» дерева поясняют, какие научные направления в той или иной мере снимают неопределенность указанного вида. Более подробно в этом пособии мы остановимся на ЗПР в условиях неопределенности факторов стохастической природы. Когда проведение эксперимента возможно, мы предлагаем рассмотреть логико-вероятностный метод (ЛВМ); в том случае, когда проведение эксперимента невозможно, снизить неопределенность поможет аппарат теории игр с природой.

Приведем два примера задач принятия решений для двух разных моделей возможных состояний среды 5.

Пример: задача принятия решений в условиях определенности — задача линейного программирования или задача оптимальной организации производства. Множество состояний среды состоит из одного элемента.

Предположим, что для производства некоторой продукции необходимо т видов сырья. На имеющемся у предприятия оборудовании можно реализовать п способов производства, различающихся между собой составом сырья, требуемого для производства единицы продукции.

Будем нумеровать способы производства индексом ] = 1,2, ..., п, а виды сырья индексом / = 1,2,..., т. Обозначим через а~ е 9? количество сырья /-го вида, необходимое для получения единицы продукции7-м способом производства. Запасы сырья ограничены величинами Ь

Единица продукции, произведенная 7-м способом производства, приносит прибыль в размере с} некоторых условных единиц (у.е.). Требуется организовать производство, чтобы получить максимальную прибыль.

п Множество альтернатив X для такой задачи будет состоять из векторов х = (х{, х2,..., хп) е 9Г, называемых планом производства. При этом имеется ряд ограничений. Во-первых, компоненты векторах должны быть неотрицательными числами. Во-вторых, величины X представляющие собой ко-

7 = 1

личества ?-го сырья, должны нс превосходить значений е 9?, / = 1, 2,т. Таким образом, множество допустимых альтернатив X будет иметь вид

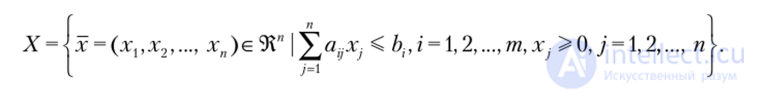
В качестве целевой функции возьмем прибыль, которую может принести план производства х = (х{, х2,..., хп) е 9?",

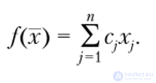
Таким образом, решением данной ЗПР будет нахождение такого плана производства (оптимального плана) х0 = (х{, х2,..., хп) е 9?”, который максимизирует прибыль при заданных ограничениях, т.е.

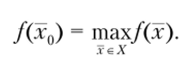
Заметим, что данная задача принятия решений может быть рассмотрена и в условиях, когда искомый план (множество планов) должен обеспечивать получение прибыли ЛПР не меньше некоторого наперед заданного (критического) значения с* е 9?, т.е. оптимальный план производства х0 = = (х,, х2,..., хп) е 9?” должен удовлетворять следующему неравенству:

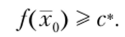
Пример: задача принятия решений в условиях вероятностной неопределенности — задача оценки эффективности инвестиционного портфеля. Множество состояний среды состоит из бесконечного, несчетного числа элементов (континуум мощности). На множестве состояний явно задана вероятность.

Пусть имеется инвестиционный портфель, содержащий два актива. Доходности от вложения единицы капитала для данных активов описываются случайными величинами %2, которые, вообще говоря, не являются стохастически независимыми.

Пусть ^ имеет равномерное распределение на отрезке [0, 12], т.е. доходность первого актива может быль любой в пределах от 0 до 12%. Пусть %2 может принимать значения 2 или 10% с вероятностями, равными 0,5, т.е. второй актив может с одинаковыми вероятностями принести либо 2%, либо 10%.

Инвестор хочет распределить единицу имеющегося у него капитала между этими активами оптимальным в некотором смысле образом.

В данной постановке задачи состояние среды является двумерным вещественным пространством 5 = 9?2 с заданной вероятностной структурой (9?2, З2, Р), где З2 — борелевская ст-алгебра, Р — совместное распределение вектора = (?р ^2). Множество альтернатив X имеет следующий вид:

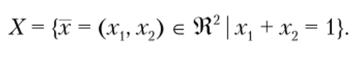
Множеством исходов решения /? будет множество значений случайной величины У являющейся средневзвешенной доходностью портфеля

Таким образом, возникает необходимость сравнения случайных доходностей. Зададим оценочную функцию ср, например, как математическое ожидание случайной средневзвешенной доходности

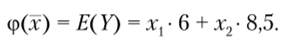
Тогда более предпочтительным решением будет выбор такого векторах, для которого среднее значение больше

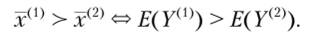
Множество наилучших решений может строиться либо как множество векторов х, при которых средняя доходность портфеля будет максимальной. Очевидно, что в данном числовом примере, так как выражение для математического ожидания ?(У) = х, • 6 + х2- 8,5 линейно зависит от (х,, х2), то следует взять (х, = 0, х2 = 1).

Не менее распространенный критерий выбора решения, когда средняя доходность портфеля будет превышать некоторое наперед заданное пороговое значение М например, М = 7%:

где Я* — множество «хороших» решений, если либо

В этом случае приемлемым управленческим решением будет всякая пара (х,, х2), такая, что

Вау!! 😲 Ты еще не читал? Это зря!

• игры с ненулевой суммой , игры с природой , принятие решений в условиях неопределенности , решение задач принятие решений ,
• принятие решений в условиях стохастической неопределенности ,
• процессы принятия решений , принятие решений ,

Исследование, описанное в статье про принятие решений в условиях неопределенности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое принятие решений в условиях неопределенности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений