13 Игры с ненулевой суммой. Игры с природой или принятие решений в условиях неопределенности,критерии, примеры решения задач

Привет, сегодня поговорим про игры с ненулевой суммой, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое игры с ненулевой суммой, игры с природой, принятие решений в условиях неопределенности, решение задач принятие решений , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

Предположим, что игрок В применяет свою активную чистую стратегию, а игрок А – свою оптимальную стратегию .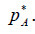

Тогда средний выигрыш игрока А будет равен:

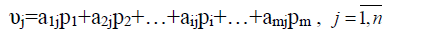
Учитывая, что υj не может быть меньше υ1, запишем условия:

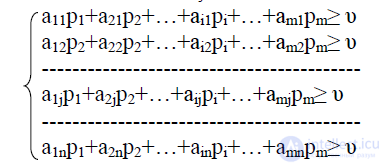
Разделим левые и правые части каждого из неравенств на цену игры , 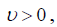получим:

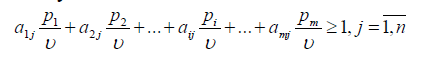
Введем новые обозначения:

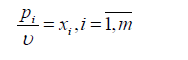
Тогда неравенства примут вид:

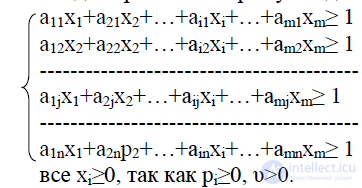
Из условия нормировки p1+p2+…+pm=1, переменные xi должны удовлетворять условию:

x1+x2+…+xi+…+xm=1/ υ .

Учитывая, что игрок А стремится максимизировать υ, получаем линейную целевую функцию:

z= x1+x2+…+xi+…+xm

Следовательно, задача решения игры свелась к следующей задаче линейного программирования: найти неотрицательные значения переменных xi, ,которые минимизируют функцию ( ) и удовлетворяют ограничениям ( ).

Из решения задачи ЛП находим цену игры υ и оптимальную стратегию 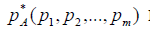игрока А:

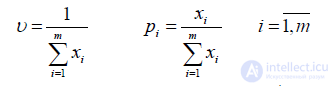
Оптимальную стратегию 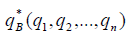игрока В находим из выражения:

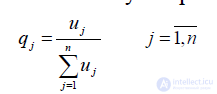
где uj – неотрицательные переменные задачи ЛП:

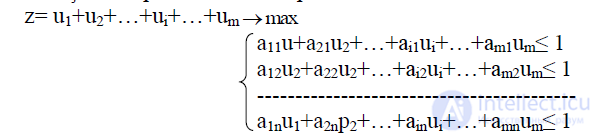
которая является двойственной по отношению к задаче, представленной условиями ( ) и ( ).

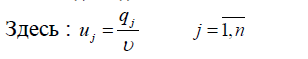
Таким образом, оптимальные стратегии и игры с платежной матрицей (aij)mxn могут быть найдены путем решения симметричной пары двойственных задач ЛП:

При этом:

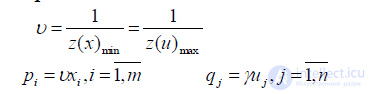
Напомним пример игры полковника Блотто.

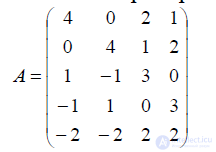
Ее можно сформулировать как задачу ЛП и решить симплекс-методом. Получим решение игры ;

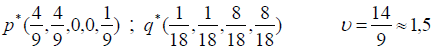
При оптимальных стратегиях полковник должен придерживаться в большей степени неравномерного распределения сил между позициями с вероятностью 4/9, а генерал – наоборот, должен придерживаться в большей степени равномерного разделения между позициями с частотами 4/9, тогда полковник получит выигрыш, оцениваемый примерно в 1,5 единицы.

Известен и обратный факт – для любой задачи ЛП может быть построена эквивалентная задача теории игр. Эта связь «теория игр – линейное программирование» оказывается полезной не только для теории игр, но и для ЛП. Иногда приближенные численные методы решения задач теории игр (при большой размерности задачи) оказываются проще, чем «классические методы» ЛП.

игры с ненулевой суммой .

Будем обозначать fk (x1,…,xN) функцию выигрыша k-го игрока (всего их N), если игрок i применяет i-ю стратегию.

В играх с ненулевой суммой равенство

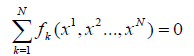
не обязательно выполняется.

Отметим сначала отличительные свойства игр двух лиц с нулевой суммой:

1) ни одному из игроков не выгодно информировать противника о своей стратегии;

2) игрокам нет никакого смысла вести переговоры до игры и уславливаться о совместном плане действий;

3) если 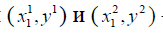- пары оптимальных стратегий первого и второго игроков соответственно, то 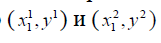– такие оптимальные пары стратегий,

при этом

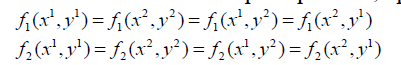
Как правило, игры с ненулевой суммой не обладают ни одним из этих свойств.

Формально игру с ненулевой суммой можно свести к игре с нулевой суммой введением (N+1)-го игрока, так называемого болвана, множество стратегий которого 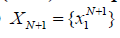состоит из одной точки и

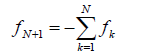
но это не приносит практических выигрышей. Для игры двух лиц с ненулевой суммой будем описывать ее так. Множества стратегий игроков будем обозначать и , при исходе первый игрок получает сумму , второй - . Тогда матрица игры будет выглядеть так:

	β1	…	βj	…	βn
α1	(f1(α1, β1),f2(α1,β1))	…	(f1(α1, βj),f2(α1,βj))	…	(f1(α1, βn),f2(α1,βn))
…	…	…	…	…	…
α i	(f1(αi, β1),f2(αi,β1))	…	(f1(αi, βj),f2(αi,βj))	…	(f1(αi, βn),f2(αi,βn))
…	…	…	…	…	…
α m	(f1(αm,β1),f2(αm,β1))	…	(f1(αm, βj),f2(αm,βj))	…	(f1(αm, βn),f2(αm,βn))

Элементы матрицы известны обоим игрокам.

В играх с нулевой суммой игроки не могут достичь обоюдной выгоды при помощи какого-либо сотрудничества, в играх же с ненулевой суммой это всегда может быть достигнуто. Важен вопрос, разрешено ли игрокам сотрудничать в игре? Под кооперативной игрой подразумевается игра, в которой имеют полную свободу сообщения до игры для составления взаимно обязывающих соглашений. В некооперативной игре не разрешено никакое сотрудничество между игроками до игры. Примером могут служить антитрестовые законы, запрещающие некоторые виды соглашений между крупными фирмами.

Пример. Два человека оказались в горящем доме. Они могут покинуть дом и спастись лишь через входную дверь. Но ее заклинило так сильно, что открыть ее можно только вдвоем. В данном случае каждый из игроков обладает двумя стратегиями:

α1 β1 – толкать дверь и пытаться ее открыть,

α2 β2 – не толкать дверь.

Действуя совместно, игроки могут спастись – выигрыш каждого равен единице, в противном случае пострадают оба – выигрыш каждого равен нулю.

	β1	β2
α1	(1, 1)	(0, 0)
α2	(0, 0)	(0, 0)

Это, во первых, кооперативная игра, во-вторых

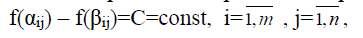
т.е. игроки выигрывают или проигрывают одновременно, это игра с постоянной разностью (в данном случае нулевой). В играх с постоянной разностью нужна координация действий игроков.

Пример. Игра «Семейный спор».

Есть матрица игры

	β1	β2
α1	(2, 1)	(-1, -1)
α2	(-1, -1)	(1, 2)

Муж (первый игрок) и жена (второй игрок) могут выбрать одно из двух вечерних развлечений: футбольный матч (α1 и β1) или балет (α2 и β2). Естественно предположить, что игрок А выберет футбол, а В – балет. Однако обоим гораздо важнее идти вместе, чем в одиночку.

Предпочтительным для первого игрока является исход (α1, β1), для второго – (α2, β2). Каждая из указанных пар является парой оптимальных стратегий: каждая стратегия одной из пар является лучше другой стратегии в той же паре:

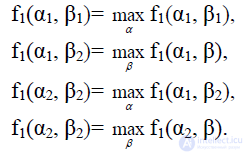
Ни (α1, β2), ни (α2, β1) не являются оптимальными парами стратегий. Более того, оптимальные пары (α1, β1) и (α2, β2) приносят игрокам неодинаковые выигрыши, т.е. эта игра не обладает свойством 3) для игр с нулевой суммой.

И первые два свойства игр с нулевой суммой тоже не выполняются, т.к. если игроки не сообщаются до игры и обладают твердыми характерами, т.е. первый выберет α1, т.к. он хочет (α1, β1), а второй выберет β2, т.к. он хочет (α2, β2), то оба проиграют. Аналогичная ситуация будет и в том случае, когда каждый из супругов имеет мягкий характер и решает уступить.

Лучшим в игре является кооперативный вариант. В этом случае, оба они будут стремиться к исходу (α1, β2) или (α2, β2), причем справедливым будет случайный выбор.

Пример. Задача Танкера или «дилемма заключенного».

Арестованы и изолированы друг от друга двое подозреваемых в совершении серьезного преступления. У прокурора нет серьезных доказательств их вины. Он сообщает каждому из задержанных о двух имеющихся альтернативах: признаться в совершении преступления (α2, β2) или не признаться (α1, β1).

	β1(Н)	β2(П)
α1(Н)	(1, 1)	(10, 1/4)
α2(П)	(1/4, 10)	(8, 8)

Если оба заключенных не признаются, то им будет предъявлено незначительное обвинение и они получат по 1 году тюрьмы. Если оба признаются, то будут осуждены, но не самым строгим образом (по 8 лет), если же один признается, а другой нет, признавшийся получит мягкий приговор, а упорствующий будет осужден на максимальный срок. Это некооперативный вариант.

(α2, β2) – не лучшая стратегия для обоих игроков.

Поскольку каждый из игроков стремится к максимальной полезности, то их разумными выборами будут α2 и β2.

Допустим, что в игре разрешена кооперация. Тогда и игроки выберут (α1, β1). Но эта пара неуравновешенна. Это ведет к возможности нарушения соглашения. Если первый игрок нарушит, а второй – нет, положение первого игрока улучшается, в противном случае – наоборот.

Здесь кооперация – невыгодна.

Оптимальное решение по Нэшу для некооперативной игры.

Стратегии называется оптимальными по Нэшу в игре N лиц с ненулевой суммой (или решением игры по Нэшу или точкой равновесия по Нэшу), если для каждого k=1,…, N.

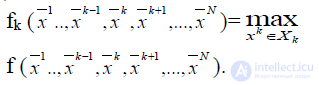
Оптимальность решения по Нэшу связана с состоянием равновесия игры, т.е. с ситуацией, в которой никому из игроков невыгодно изменять свою стратегию. В рассмотренной игре «семейный спор» пары (α1, β1); (α2, β2) являются решением по Нэшу, в игре «дилемма заключенного» таковой является пара (α2, β2).

Как и в играх с нулевой суммой игра с ненулевой суммой может не иметь решения по Нэшу в чистых стратегиях.

Теорема Нэша. Любая некооперативная игра N лиц с ненулевой суммой имеет по крайней мере одно решение по Нэшу в классе смешанных стратегий.

Рассмотрим проблему принятия решений в некооперативной игре двух игроков с точки зрения третьего лица – «арбитра». Какими характеристиками должно обладать хорошее решение игрока? Во-первых, свойством эффективности по получаемым игроками выигрышам, во-вторых, свойством устойчивости решения. С позиций нейтрального лица игра двух лиц с целевыми функциями:

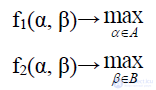
может рассматриваться как многокритериальная на множестве L=A×B. Аргументом при этом является вектор 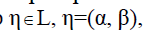, а задача приобретает вид:

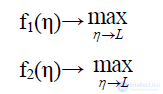
Для выбора эффективных решений используется принцип Парето. Парето – оптимальные или эффективные решения обладают тем свойством, что улучшить выигрыш одного из игроков можно только за счет уменьшения выигрыша других игроков. Ясно, что решение, находящееся вне множества Парето (переговорного множества) может быть улучшено сразу для всех игроков. На переговорном множестве интересы игроков антагонистичны.

Сложность в том, что выбор η осуществляется не одним лицом, а несколькими. И тут приобретает значение принцип Нэша: выбор рациональной стратегии должен производиться среди точек равновесия по Нэшу.

Возникает противоречие между оптимальностью решения по Парето и оптимальностью по Нэшу, т.е. противоречие между выгодностью и устойчивостью.

Только в случае, когда устойчивые решения являются одновременно паретовскими, можно эффективно использовать принцип Нэша.

Пример. К нерегулируемому перекрестку едут на высокой скорости под прямым углом друг к другу два автомобиля. У каждого водителя есть две стратегии:

- α1, β1 – снизить скорость до безопасной (Б)

- α2, β2 – продолжать ехать на высокой скорости (рискованная стратегия - P).

Если оба водителя будут придерживаться стратегии Б, это приведет к благополучному исходу, оцениваемому для каждого числом 1. Если оба выбирают рискованную стратегию, то происходит авария и проигрыш оценивается в (-9). При других комбинациях (Б, Р), (Р, Б) исход оценивается 0 для снизившего скорость (за потерю времени) и числом 3 для не снизившего (за экономию времени).

	β1(Б)	β2(Р)
α1(Б)	(1, 1)	(0, 3)
α2(Р)	(3, 0)	(-9, -9)

Ситуации (Б, Б) и (Р, Р) очевидно неустойчивы, т.к. каждый игрок может односторонним решением выиграть больше. Ситуации (Б, Р) и (Р, Б) обе устойчивы. Оптимальной по Порето не является ситуация (Р, Р). Т.е. в задаче есть две ситуации (Б, Р), (Р, Б) оптимальные одновременно и по Порето и по Нэшу.

Для игры «дилемма заключенного» решение (П, П) устойчиво по Нэшу, но не оптимально по Парето

игры с природой или принятие решений в условиях неопределенности .

В задачах теории игр, рассматривая операции, производимые в условиях неопределенности, мы эту неопределенность связывали с поведением противника (или противников). Об этом говорит сайт https://intellect.icu . При этом предполагалось автоматически, что противник является разумным (принцип равной разумности), что он действует осознанно, выбирая для себя именно те действия, которые невыгодны для нас, т.е. образно говоря, считали, что противник «злонамерен». Однако, очень часто неопределенность, сопровождающая некоторую операцию, не связана с сознательным поведением противника, а зависит только от некой неизвестной игроку А объективной действительности, от неинформированности об объективной ситуации. Неопределенность такого типа может быть связана с различными причинами: сложность ситуации, которую довольно сложно оценить, рыночная конъюнктура, изменение спроса, политика правительства, надежность партнера, отказы оборудования, курс валют, уровень инфляции, экономическая обстановка, стихийные бедствия.

Такого рода ситуации принято называть играми с природой (часто с Природой, Nature). Второй игрок в данном случае называется природой и в теории игр не является целенаправленным, сознательным игроком. Он рассматривается как некоторая незаинтересованная инстанция. Возможные стратегии природы, ее состояния реализуются случайным образом.

Таким образом, в игре с природой действует только один игрок, он же игрок А, он же исследователь операции, он же лицо принимающее решение. Природа П является вторым игроком, но не противником игрока А. игрока А в игре с природой иногда называют статистиком, а торию игр с природой – теорией статистических решений.

Пусть игроку А необходимо выполнить операцию в неизвестной обстановке, относительно состояний которой можно сделать n предположений П1, П2, …, Пn. Эти предположения будем рассматривать как стратегии природы. Игрок А имеет в своем распоряжении m возможных стратегий А1, А2, …, Аm. Выигрыши игрока А аij при каждой паре стратегий предполагаются известными и задаются платежной матрицей А=||aij|| (или матрицей выигрышей). Задача заключается в определении такой стратегии (чистой или смешанной), которая обеспечила бы игроку наибольший выигрыш.

Природа может принимать одно из своих возможных состояний и не имеет целью получение выигрыша Игра с природой представляется в виде платежной матрицы, элементы которой – выигрыши игрока А, но не являются проигрышами природы П. Матрица еще называется матрицей доходности, которая агрегирует информацию о возможной доходности вариантов стратегии при различных сценариях развития экономической ситуации

Различают два вида задач в играх с природой:

1.Задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы

2.Задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний

1.Уникальные единичные случайные явления связаны с неопределенностью.

2.Массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.

3.Ситуация с полной неопределенностью характеризуется отсутствием какой бы то ни было дополнительной информации.

3.1 Игровые модели в условиях неопределенности

Предположим, что лицо, принимающее решение, может выбрать одну из возможных альтернатив, обозначенных номерами i = 1, 2, …, m Ситуация является полностью неопределенной, т. е. известен лишь набор возможных вариантов состояний внешней (по отношению к лицу, принимающему решение) среды, обозначенных номерами j = 1, 2, …, n

Если будет принято i-e решение, а состояние внешней среды соответствует j-й ситуации, то лицо, принимающее решение, получит доход

Необходимо провести оценку риска в условиях, когда реальная ситуация неизвестна. Если игрок знает, что осуществляется j-е состояние природы, то выбрал бы наилучшее решение, то есть то, которое принесет наибольший выигрыш

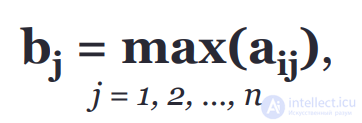
Принимая i-e решение, игрок А рискует получить не bj , а только aij, то есть, если игрок примет i-е решение, а в природе реализуется j-е состояние, то произойдет недополучение дохода в размере:

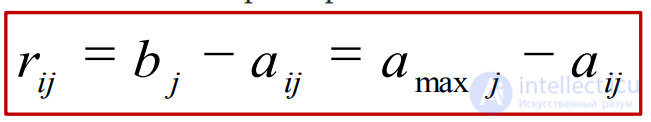
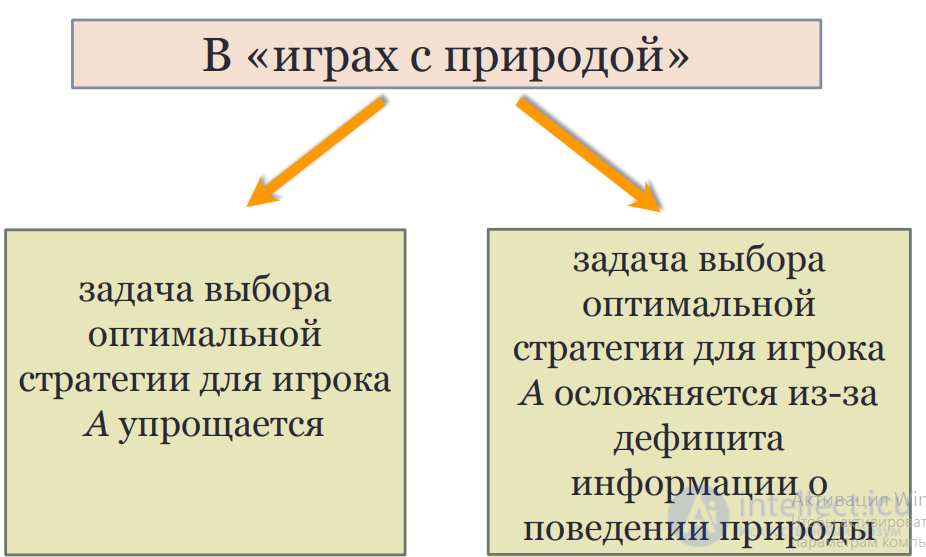
(по сравнению с тем, как если бы игрок знал точно, что реализуется j-е состояние природы, и выбрал бы решение, приносящее наибольший доход bj = max(aij), j = 1, 2, …, n)

aij – значение показателя доходности варианта стратегии с максимальной доходностью из имеющихся i-ых вариантов при наступлении j-ого сценария развития событий

amaxj - значение показателя доходности i-ого варианта стратегии при наступлении j-ого сценария развития событий (элемент платежной матрицы)

Матрица рисков (сожалений) отражает риск реализации вариантов стратегии для каждой альтернативы развития событий (характеризует риск выбора определенного варианта стратегии), который будет зависеть от уровня риска варианта стратегии при наступлении различных сценариев.

При решении Задачи о принятии решений в условиях неопределенности для отбора вариантов стратегии применяют так называемые критерии оптимальности (альтернативные критерии оптимальности):

- критерий Вальда,

- критерий оптимизма,

- критерий пессимизма,

- критерий Сэвиджа,

-критерий Гурвица

Для выбора наиболее эффективного варианта стратегии ко всем возможным вариантам развития применяются все критерии оптимальности одновременно: каждый из критериев позволяет отобрать только один вариант, оптимальным же будет являться тот из них, на который указало большинство критериев.

1) Критерий Вальда (критерий гарантированного результата, максиминный критерий) позволяет выбрать наибольший элемент матрицы доходности из ее минимально возможных элементов:

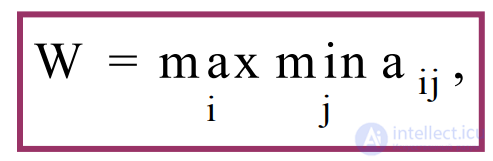
aij– элемент матрицы доходност

Критерий Вальда предназначен для выбора из рассматриваемых вариантов стратегий варианта с наибольшим показателем эффективности из минимально возможных показателей для каждого из этих вариантов.

Данный критерий обеспечивает максимизацию минимального выигрыша, который может быть получен при реализации каждого из вариантов стратегий. Критерий ориентирует лицо, принимающее решение, на осторожную линию поведения, направленную на получение дохода и минимизацию возможных рисков одновременно.

Применение критерия Вальда оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

о вероятности наступления того или иного состояния природы ничего не известно;

не допускается никакой риск;

реализуется лишь малое количество решений.

Пример задачи с применением критерия Вальда

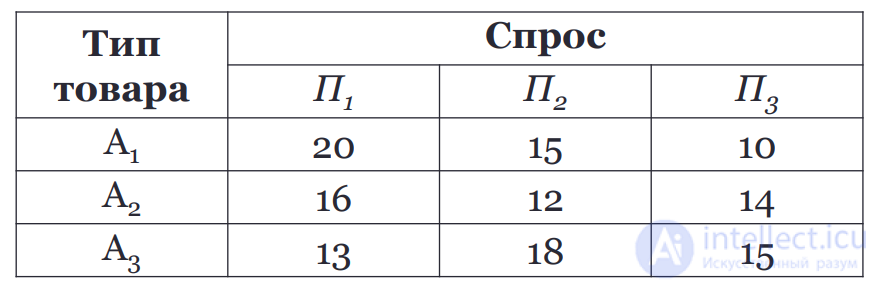
Найти оптимальную стратегию по критерию Вальда.

Решение:

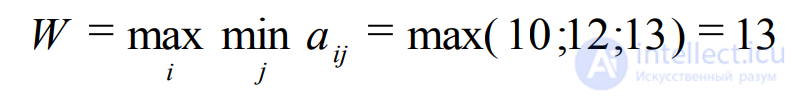
Полученный результат соответствует стратегии А3

2) Критерий оптимизма (критерий максимакса) предназначен для выбора наибольшего элемента матрицы доходности из ее максимально возможных элементов:

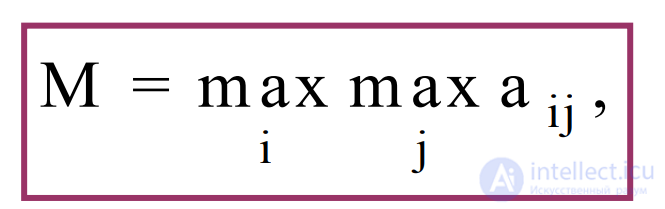
Критерий оптимизма используется, когда игрок оказывается в безвыходном положении, когда любой его шаг равновероятно может оказаться как абсолютным выигрышем, так и полным провалом.

Данный критерий предполагает, что развитие ситуации будет благоприятным для лица, принимающего решение. Вследствие этого, оптимальным выбором будет вариант с наибольшим значением показателя эффективности в матрице доходности.

Ценой игры в чистых стратегиях по критерию оптимизма (М) является наибольший из показателей эффективности чистых стратегий

пример Найти оптимальную стратегию по критерию оптимизма.

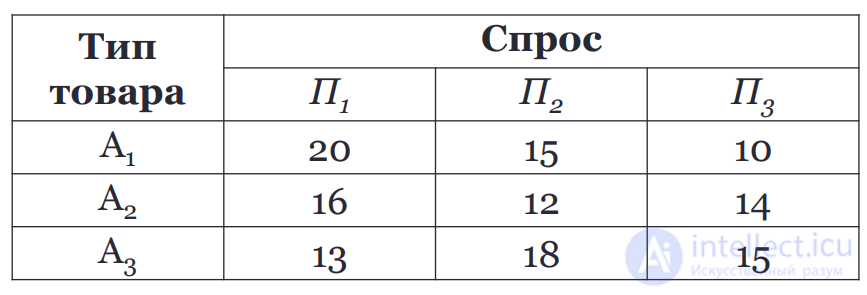
Решение:

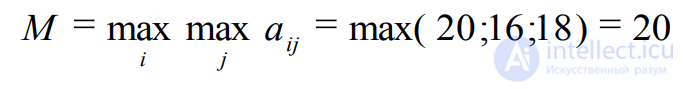
Полученный результат соответствует стратегии А1

3) Критерий пессимизма предназначен для выбора наименьшего элемента матрицы доходности из ее минимально возможных элементов:

Критерий пессимизма предполагает, что развитие ситуации будет неблагоприятным для лица, принимающего решение.

При использовании этого критерия лицо принимающее решение ориентируется на возможную потерю контроля над ситуацией и, поэтому, старается исключить все потенциальные риски и выбрать вариант с минимальной доходностью.

Пример: Найти оптимальную стратегию по критерию пессимизма.

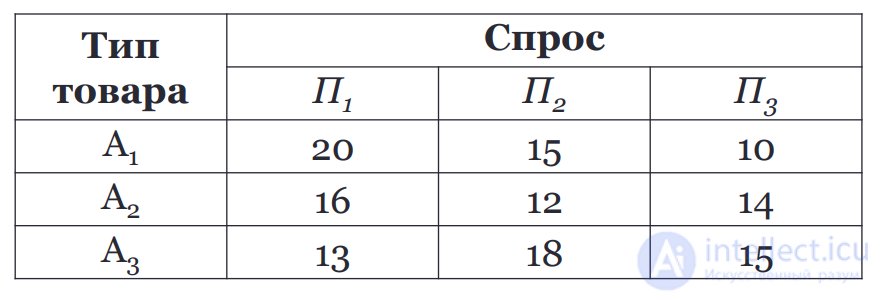
Решение:

Полученный результат соответствует стратегии А1

Миниминный критерий относительно рисков (μ-критерий). Показателем неэффективности стратегии Аi игрока А считается наименьший риск при выборе этой стратегии и обозначается через μ.

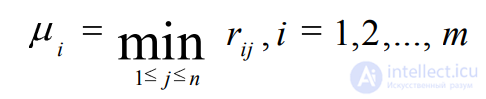
где rij – матрица рисков.

Поскольку риски неотрицательны, то и μкритерий это величина неотрицательная, т.е. μi ≥ 0, i = 1, 2,…, m. Таким образом:

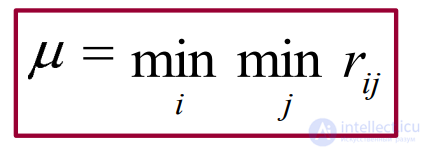
Чистая стратегия относительно рисков является μ оптимальной, если соответствующая ей строка матрицы рисков содержит хотя бы один ноль.

μ-критерий является критерием крайнего оптимизма по отношению к рискам, так как игрок предполагает, что природа будет к нему благосклонна и будет находиться в благоприятном для него состоянии, при котором риск будет сведен к нулю.

4) Критерий Сэвиджа (критерий минимаксного риска Сэвиджа) предназначен для выбора максимального элемента матрицы рисков из ее минимально возможных элементов:

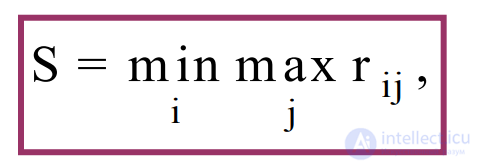
Среди элементов матрицы рисков сначала выбирается максимальный риск при каждой стратегии, а затем из них выбирается минимальный. То есть в данном случае пессимистично настроенный игрок предполагает, что состояние природы будет таковым, что для любой его стратегии риск будет наибольшим, а стратегию выбирает такую, чтобы этот риск минимизировать.

Критерий Сэвиджа позволяет выбрать вариант стратегии с меньшей величиной риска по сравнению с более высоким, первоначально ожидаемым уровнем риска. Данный критерий ориентирует лицо принимающее решение на более благоприятное развитие ситуации по сравнению с наихудшим состоянием, на которое то рассчитывало вначале

Ценой игры в чистых стратегиях по критерию Сэвиджа называется минимальный показатель неэффективности среди показателей неэффективности всех чистых стратегий.

Теорема: Для того чтобы чистая стратегия была безрисковой, т.е. чтобы ее показатель неэффективности по критерию Сэвиджа был нулевым, необходимо и достаточно, чтобы она доминировала каждую из остальных чистых стратегий.

Пример: Найти оптимальную стратегию по критерию Сэвиджа.

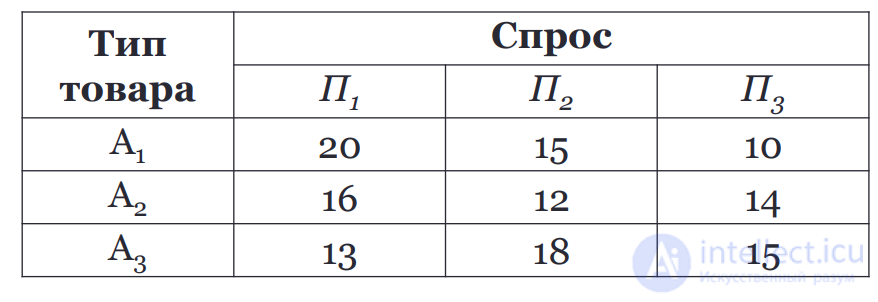
Решение: Применяем формулу rij = a maxj - a i j, построим матрицу рисков. Матрица рисков

Полученный результат соответствует стратегии А3

5) Критерий Гурвица (взвешивает пессимистический и оптимистический подходы к анализу неопределенной ситуации) предназначен для выбора некоторого среднего элемента матрицы доходности, отличающегося от крайних состояний – от минимального и максимального элементов:

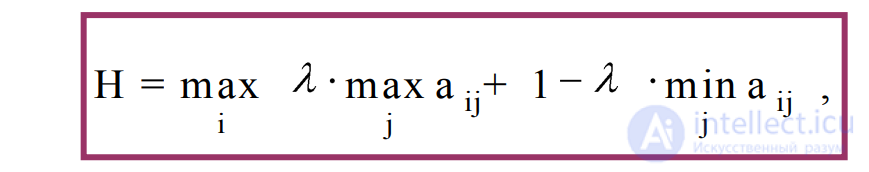
где λ – коэффициент оптимизма, 0 < λ<1

Коэффициент λ выражает количественно «меру оптимизма» игрока А при выборе стратегии и определяется им из субъективных соображений на основе статистических исследований результатов принятия решений или личного опыта лица принимающего решение в схожих ситуациях.

1. Если λ → 1, то правило Гурвица приближается к правилу Вальда

2. Если λ → 0, то правило Гурвица приближается к правилу оптимизма

если λ коэффициент оптимизма, то (λ – 1) коэффициент пессимизма

Критерий Гурвица позволяет избежать пограничных состояний при принятии решения – неоправданного оптимизма и крайнего пессимизма относительно ожидаемой доходности – и выбрать наиболее вероятный вариант стратегии, обеспечивающий наилучшую эффективность.

Критерий Гурвица ориентирован на установление баланса между случаями крайнего пессимизма и крайнего оптимизма при выборе стратегии путем взвешивания обоих исходов с помощью коэффициента оптимизма

Пример:Найти оптимальную стратегию по критерию Гурвица. λ = 0,5

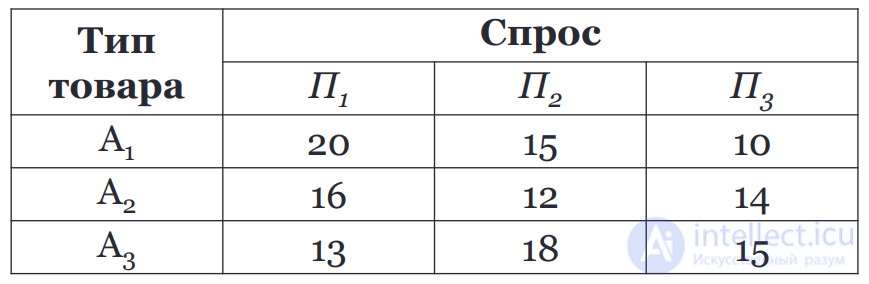
Решение:

Полученный результат соответствует стратегии А3

3.3.3 Принятие решений в условиях риска

При решении Задачи о принятии решений в условиях риска различным состояниям природы поставлены в соответствие соответствующие вероятности. Игрок А принимает решение на основе критерия максимального ожидаемого среднего выигрыша или минимального ожидаемого среднего риска

Критерии оптимальности в условиях риска

:  критерий Байеса;

 критерий Лапласа;

 критерий максимальной вероятности

1) Критерий Байеса относительно выигрышей Предположим, что игроку А известны не только состояния П1 , П2 ,…Пn в которых случайным образом может находиться природа, но и вероятности (q1 , q2 ,…qn ) наступления этих состояний, при этом ∑qj = 1. Это говорит о том, что лицо принимающее решение находится в условиях риска.

Матрицу выигрышей игрока А и вероятности состояний природы П можно представить в виде общей матрицы

Чистую стратегию Аi можно определить как случайную величину со следующим законом распределения

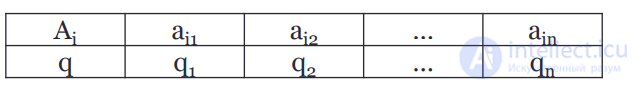
Математическое ожидание данной случайной величины

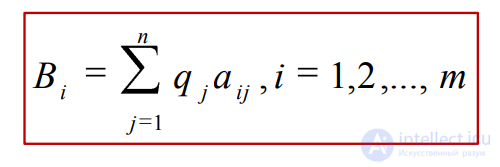
Оно означает средне взвешенное выигрышей i-ой строки матрицы А с весами (q1 , q2 ,…qn )

Критерий Байеса относительно выигрышей позволяет выбрать максимальный из ожидаемых элементов матрицы доходности при известной вероятности возможных состояний природы:

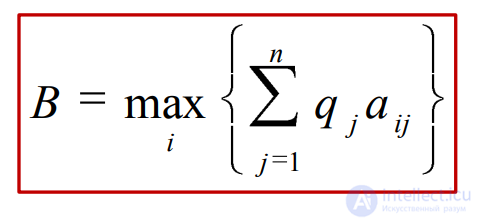
2) Критерий Байеса относительно рисков Матрицу рисков игрока А и вероятности состояний природы П можно представить матрицей:

Показателем эффективности стратегии Аi по критерию Байеса относительно рисков является математическое ожидание рисков, расположенных в i-ой строке матрицы R.

Критерий Байеса относительно рисков позволяет выбрать минимальное значение из средних рисков при известной вероятности возможных состояний природы:

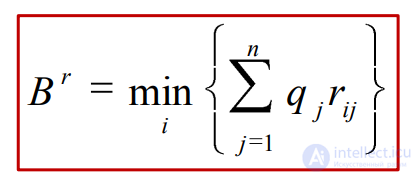
Критерии Байеса относительно выигрышей и относительно рисков эквивалентны, то есть по обоим критериям оптимальной будет одна и та же стратегия

3) Критерий Лапласа относительно выигрышей Вероятность состояний природы оценивается субъективно как равнозначные.

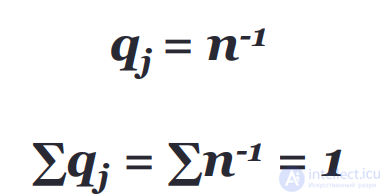
Этот принцип называется – принцип недостаточного основания Лапласа.

Имеется игра с природой, в которой игрок А обладает m чистыми стратегиями Аi , природа П может случайным образом находиться в одном из n своих состояний Пj , а матрица выигрышей игрока А задается следующим образом:

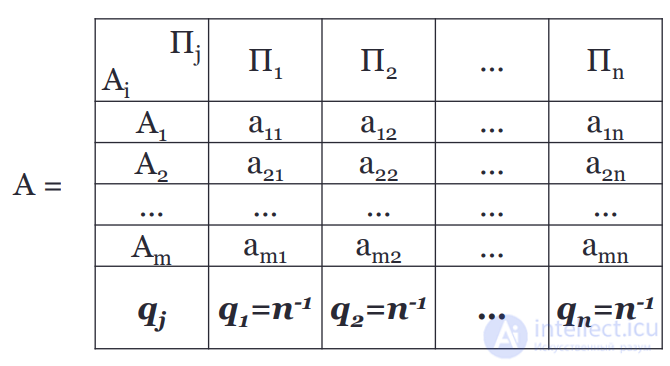
Показателем эффективности чистой стратегии Аi по критерию Лапласа относительно выигрышей является среднеарифметическое выигрышей при этой стратегии.

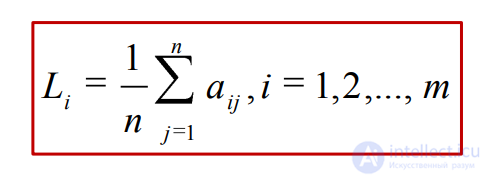
Критерий Лапласа относительно выигрышей предполагает выбор варианта стратегии с максимальной ожидаемой доходностью при равной вероятности наступления возможных стратегий природы.

4) Критерий Лапласа относительно рисков

Матрицу рисков игрока А и вероятности состояний природы П при критерии Лапласа относительно рисков можно представить матрицей:

Показателем неэффективности чистой стратегии Аi по критерию Лапласа относительно рисков является среднеарифметическое рисков при этой стратегии

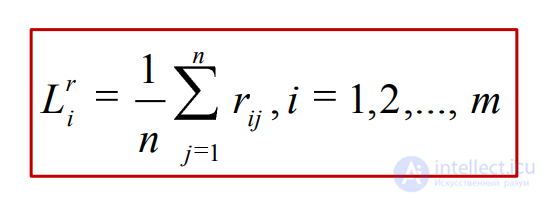
Критерий Лапласа относительно рисков предполагает выбор варианта стратегии с минимальным риском при равной вероятности наступления возможных состояний природы

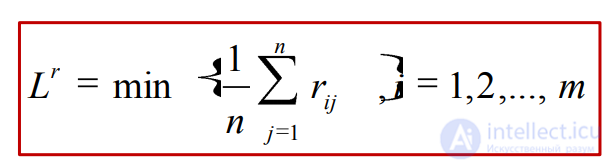
Критерий максимальной вероятности Рассмотрим игру с природой размера m x n, где m ≥ 2 и n ≥ 2. Известны вероятности qj состояний природы Пj

Максимальная вероятность обозначается следующим образом

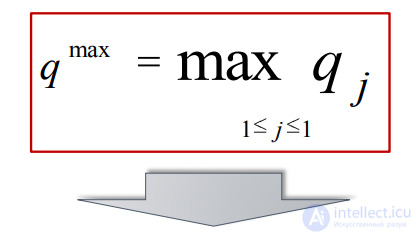
Максимальную вероятность может иметь не одно состояние природы. А также максимальное значение может быть у всех состояний природы при равных вероятностях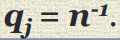

Предположим, что состояния природы Пjκ, κ = 1,2,…σ, где σ – это номер состояний природы (столбцы), имеющих максимальную вероятность.

Показателем эффективности чистой стратегии Аi по критерию максимальной вероятности относительно выигрышей, является наибольший выигрыш из выигрышей при этой стратегии и при состояниях природы Пjκ κ = 1,2,…σ, имеющих максимальную вероятность q max .

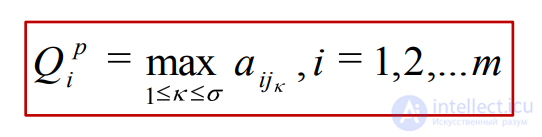
В связи с этим рассматривается матрица m x σ, которая получается путем исключения тех столбцов, у которых вероятности ниже максимального значения.

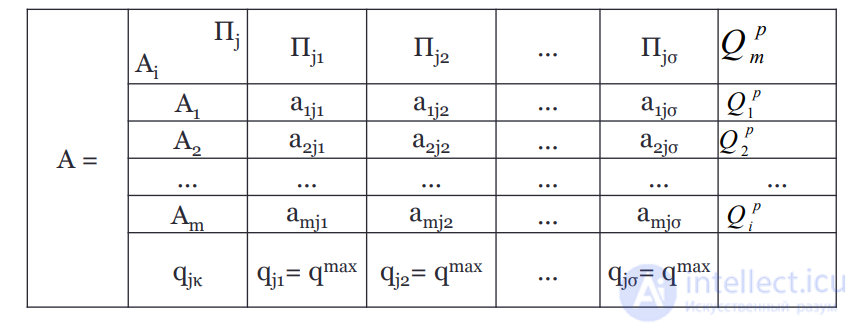
Ценой игры (Qp ) при критерии максимальной вероятности относительно выигрышей будет наибольший элемент из показателей эффективности

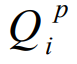
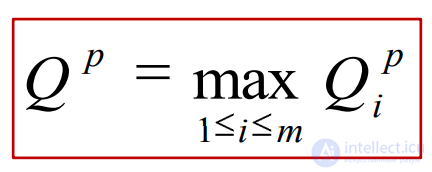
Рассмотрим случай, когда максимальную вероятность имеет только одно состояние природы, то есть σ = 1. Тогда матрица m x σ превращается в j 1 – й столбец, при которой выигрыш akj1 – наибольший среди состояний природы Пj1 .

Пример:Найти оптимальную стратегию по критерию максимальной вероятности относительно выигрышей при вероятностях состояний природы

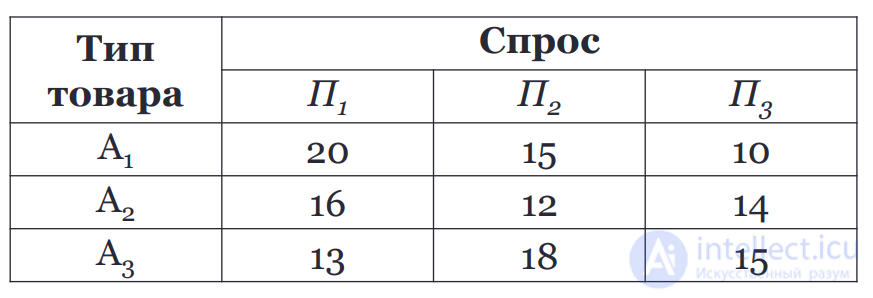
q1 = 0,2; q2 = 0,3; q3 = 0,5.

Другие примеры

Пример1.Студент , войдя в троллейбус, решает брать ли билет. Исход определяется двумя обстоятельствами: решением студента и возможным поведением контролера. Студент выступает в роли игрока, а факт появления контролера – в качестве состояния природы.

	Состояние природы
	Контролер появится	Контролер не появится
Брать билет	-2 у.е.	-2 у.е.
Не брать билет	-8 у.е.	0 у.е.

Оценки выигрыша указаны в платежной матрице.

Анализ матрицы игры с природой и проще и сложнее анализа матрицы антагонистической игры. Ввиду того, что природа не противодействует статистику, может оказаться, что игра с природой проще стратегической игры. На самом деле это не так. Противоположность интересов и игроков как бы снимает неопределенность, чего нельзя сказать об игре с природой. С другой стороны, оперирующей стороне легче в игре с природой в том смысле, что он выиграет скорее всего больше, чем в игре с разумным противником. Однако решение принять труднее, особенно обоснованное решение, т.к. неопределенность в игре с природой сказывается в гораздо большей степени.

Целесообразно не только оценить выигрыш в той или иной игровой ситуации, но и определить разность между максимально возможным выигрышем для данного состояния природы и выигрышем, который будет получен при применении стратегии Ai в тех же условиях. Эта разность в теории игр называется риском.

Максимальный выигрыш в j-м столбце обозначим через βj, т.е. βj=. Величина βj характеризует благоприятность состояния природы. Риск игрока при применении им стратегии Ai в условиях Пj обозначим через rij. Тогда rij= βj – аij, где rij≥0.

Матрица рисков R=||rij||m×n во многих случаях позволяет более глубоко понять неопределенность ситуации, чем платежная матрица.

βj называется показателем благоприятности состояния Пj природы для увеличения выигрыша. Благоприятность состояния природы рассматривается как фактор, благоприятствующий увеличению игрока А. Риск rij игрока А при применении им стратегии Аi в условиях состояния природы Пj есть упущенная им возможность максимального выигрыша βj (невыигранная часть выигрыша βj).

Пример 2. Планируется операция в заранее неясных условиях, касающихся, например, конъюнктуры рынка: П1, П2, П3, П4.

Выгодность операции (ожидаемая прибыль) задана матрицей выигрышей.

Bj Ai	П1	П2	П3	П4
А1	1	4	5	9
А2	3	8	4	3
А3	4	6	6	2

β1=4 β2=8 β3=6 β4=9

Получим матрицу рисков:

Bj Ai	П1	П2	П3	П4
А1	3	4	1	0
А2	1	0	2	6
А3	0	2	0	7

Во второй строке а21=а24=3. При состоянии природы П1 выбор а21 почти совершенно хорош, а вот при состоянии природы П4 выбор стратегии А2 очень плох.

Критерии для принятия решений в играх с природой.

Критерий, основанный на известных вероятностях состояний природы (Критерий Байеса).

Предположим, что статистику из прошлого опыта известны не только состояния природы, П1, П2, …, Пn, в которых может находиться природа, но и соответствующие вероятности, с которыми природа реализует эти состояния.

Показателем эффективности стратегии Аi по критерию Байеса называется среднее значение или математическое ожидание выигрыша i-й строки:

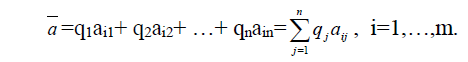
Т.е. 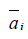- взвешенное среднее выигрышей i-й строки, взятых с весами q1, q2,…, qn

Оптимальной по критерию Байеса считается стратегия с максимальным показателем эффективности , т.е.

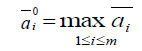
Вернемся к примеру с билетом

Пj Ai	П1(q1)	П2(q2=1- q1)
A1	-2	-2
A2	-8	0

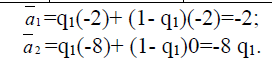
Согласно критерию Байеса следует предпочесть стратегию А1 («брать билет»), если -2>-8q1, т.е. если q1>1/4. В противном случае следует предпочесть стратегию А2. Если считать, что каждый вагон имеет равные шансы посещения контролером, а число вагонов k и контролеров r (r≤k), можно положить, что q1≈r/k. Т.о. если на трамвайный вагон приходится более 1 контролера, выгоднее брать билет!

Можно показать, что 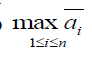эквивалентен критерию:

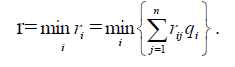
Т.е. критерий Байеса минимизирует средний риск.

Еще одно важное положение: когда известны вероятности состояний природы q1, q2, …, qn игроку А нет смысла пользоваться смешанными стратегиями. Действительно, если игрок применит смешанную стратегию pA=(p1, p2, …, pm), то средний выигрыш будет:

Но не может быть больше максимальной из осредняемых величин, т.е. max ai. Т.е. применение любой смешанной стратегии pA не может быть выгоднее для игрока А, чем применение оптимальной чистой стратегии.

Критерий Лапласа.

Часто состояния природы нельзя оценить даже из предыдущего опыта, или это стоит очень дорого (привлечение экспертов и аналитиков). Тогда применяется следующий принцип: мы не можем отдать предпочтение ни одному из состояний природы, а поэтому считаем их равновероятными, то есть q1=q2=…=qn=1/n. Этот принцип называется принципом недостаточного основания Лапласа. На нем основан критерий Лапласа.

Показателем эффективности стратегии Ai по критерию Лапласа называется среднее арифметическое выигрышей i-й строки:

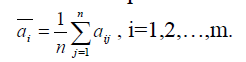
Оптимальной по критерию Лапласа считается стратегия , показатель эффективности которой максимален.

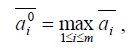
Очевидно, что критерий Лапласа есть частный случай критерия Байеса при q1=q2=…=qn=1/n.

Иногда, если мы знаем, какие состояния природы более вероятны, а какие мене, но насколько – не знаем, можно назначить вероятности состояний, пропорциональными членам убывающей арифметической прогрессии

q1:q2:q3:…qn=n:(n-1):…:1,

или с учетом того, что q1+q2+q3+…+qn=1,

,

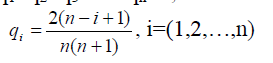
Критерий Вальда (максиминный критерий или критерий крайнего пессимизма).

Критерий Вальда основан на гипотезе антагонизма. Она состоит в предположении, что среда ведет себя «наихудшим» образом для игрока.

В соответствии с критерием Вальда выбирается та стратегия, для которой показатель эффективности

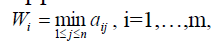(минимум строки)

а стратегия .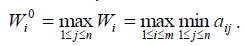

Оптимальная стратегия по Вальду гарантирует при любых состояниях природы выигрыш, не меньший чем максимин. Число называют гарантированной оценкой, а критерий Вальда иногда называют критерием гарантированного результата.

Критерий Вальда ориентирует игрока на крайне осторожное, осмотрительное поведение. Поэтому он называется критерием крайнего пессимизма.

Часто критерием Вальдта пользуются и в обиходе, что подтверждается пословицами: «Семь раз отмерь – один раз отрежь», «Береженого Бог бережет», «Лучше синица в руках, чем журавль в небе».

Критерий максимакса (критерий крайнего оптимизма или критерий азартного игрока).

Показатель эффективности стратегии Ai по этому критерию:

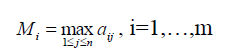, (максимум строки)

В качестве эффективной стратегии по этому критерию является стратегия с максимальным показателем эффективности

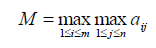
Это критерий максимального оптимизма, гарантирующий игроку максимальный выигрыш. Он соответствует поговоркам: «Пан или пропал», «Кто не рискует, тот не выигрывает», «Плох тот солдат, кто не мечтает стать генералом».

Критерий Сэвиджа (критерий крайнего пессимизма, критерий минимального риска).

Оптимальная стратегия по Сэвиджу минимизирует максимальный риск

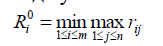
Критерии Вальда и Сэвиджа неэквивалентны (покажем ниже). Критерий Сэвиджа выражает сожаление о том, насколько выбранная стратегия не оказалась наилучшей. По сравнению с критерием Вальда в нем придается большее значение все-таки выигрышу, а не проигрышу.

Критерий Гурвица. (критерий обобщенного максимума или критерий пессимизма-оптимизма).

В критерии Гурвица вводится показатель оптимума .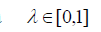

Оптимальной считается стратегия:

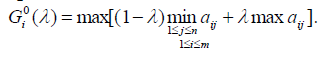
Платежная матрица дополняется столбцом, содержащим средневзвешенное наименьшего и наибольшего результатов для каждой строки. Выбираются те варианты, в строках которых стоят наибольшие элементы этого столбца.

При =1 критерий Гурвица превращается в критерий максимаксный, а при =0 – критерий Вальда. Чем больше к единице, тем больше оптимизма и пессимизма. Выбор достаточно сложен. На практике используют =0,3 – 0,7. Чем опаснее ситуация, тем более должно быть ближе к единице, тем больше надо подстраховаться.

Пример. Для защиты информации от программных воздействий Пj разработаны три программных продукта A1,A2,A3.

Матрица эффективности выглядит так:

Пj Ai	П1	П2	П3	П4
A1	0,1	0,5	0,1	0,2
A2	0,2	0,3	0,2	0,4
A3	0,1	0,4	0,4	0,3

Например: П1 – сетевые вирусы, П2 – попытки несанкционированного доступа, П3 – хакерские атаки, П4 – копирование.

1) Критерий Байеса. Считаем, что известны

q1=0,4 , p2=0,2 , q3=0,1 , q4=0,3

K(A1)=0,4*0,1+0,2*0,5+0,1*0,1+0,3*0,2=0,21

K(A2)=0,4*0,2+0,2*0,3+0,1*0,2+0,3*0,4=0,28

K(A3)=0,4*0,1+0,2*0,4+0,1*0,4+0,3*0,3=0,25

Оптимальное решение – A2.

2) Критерий Лапласа.

q1=q2=q3=q4=1/n=0,25

K(A1)=0,25(0,1+0,5+0,1+0,2)=0,225

K(A2)=0,25(0,2+0,3+0,2+0,4)=0,275

K(A3)=0,25(0,1+0,4+0,4+0,3)=0,3

По критерию Лапласа – оптимальное решение - A3.

3) Критерий Вальда

K(A1)=min(0,1; 0,5; 0,1; 0,2)=0,1

K(A2)=min(0,2; 0,3; 0,2; 0,4)=0,2

K(A3)=min(0,1; 0,4; 0,4; 0,3)=0,1

Оптимальное решение - A2.

4) Критерий азартного игрока

K(A1)=max(0,1; 0,5; 0,1; 0,2)=0,5

K(A2)=max(0,2; 0,3; 0,2; 0,4)=0,4

K(A3)=max(0,1; 0,4; 0,4; 0,3)=0,4

5) Критерий Сэвиджа

Матрица потерь

rij

Пj Ai	П1	П2	П3	П4
A1	0,1	0	0,3	0,2
A2	0	0,2	0,2	0
A3	0,1	0,1	0	0,1

K(A1)=max(0,1; 0; 0,3; 0,2)=0,3

K(A2)=max(0; 0,2; 0,2; 0)=0,2

K(A3)=max(0,1; 0,1; 0; 0,1)=0,1

Оптимальное решение – A3. (Не совпадает с Вальдом).

6) Критерий Гурвица

Возьмем =0,6

K(A1)=0,6*0,5+(1-0,6)*0,1=0,34

K(A2)=0,6*0,4+(1-0,6)*0,2=0,32

K(A3)=0,6*0,4+(1-0,6)*0,1=0,28

Оптимальный вариант – A1.

Сравнительные результаты:

Ai	K(Ai)
	Байес	Лаплас	Вальд	Максимакс	Гурвиц	Сэвидж
A1	0,21	0,225	0,1	0,5	0,34	0,3
A2	0,28	0,275	0,2	0,4	0,32	0,2
A3	0,25	0,300	0,1	0,4	0,28	0,1

Что же выбрать?

На выбор критерия влияет ряд факторов:

• - природа конкретной ситуации и ее цель (в одних операциях риск допустим, в других – нужен гарантированный результат);
• - причины неопределенности (действительно ли действует природа, ил все-таки сознательный противник);
• - характер лица, принимающего решение (одни люди склонны к риску в надежде на успех, другие всегда действуют осторожно).
• Как оценить склонность к риску, оптимизм, пессимизм?

Проводится лотерея. Стоимость билета 10 у.е. За эти деньги игрок с равной вероятностью (p=0,5) может ничего не выиграть или выиграть 100 у.е. Один человек просто не купит билет, другой готов заплатить за него 50, или даже 60 у.е. – третий.

Безусловным денежным эквивалентом (БДЭ) игры называется максимальная сумма денег, которую ЛПР готово заплатить за участие в лотерее, или минимальная сумма денег, за которую он готов отказаться от игры. Каждый индивид имеет свой БДЭ.

Индивида, для которого БДЭ совпадает с ожидаемой денежной оценкой (ОДО), то есть с ценой игры, со средним выигрышем, условно называют объективистом, индивида, для которого БДЭ≠ОДО – субъективистом. ОДО рассматривается как цена игры (по критерию Байеса-Лапласа). Если субъективист склонен к риску, то его БДЭ>ОДО (оптимист, азартный игрок), если же не склонен, БДЭ<ОДО (пессимист, осторожный игрок).

Вау!! 😲 Ты еще не читал? Это зря!

• принятие решений в условиях стохастической неопределенности ,
• процессы принятия решений , принятие решений ,
• принятие решений в условиях неопределенности ,

Надеюсь, эта статья об увлекательном мире игры с ненулевой суммой, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое игры с ненулевой суммой, игры с природой, принятие решений в условиях неопределенности, решение задач принятие решений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.