9 Алгоритм решения транспортной задачи, виды методов решения

Привет, сегодня поговорим про алгоритм решения транспортной задачи, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое алгоритм решения транспортной задачи, транспортная задача, метод потенциалов , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида Ее можно рассматривать как задачу об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.

Транспортная задача по теории сложности вычислений входит в класс сложности P. Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).

Постановка задачи

Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределенном количестве) со статичными данными и линеарном подходе (это основные условия задачи).

Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить ее решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.

Математическая формулировка задачи

Пусть имеется пунктов производства некоторого однородного продукта и пунктов его потребления. Для каждого пункта производства и для каждого пункта потребления заданы следующие величины: объем производства в пункте производства , объем потребления в пункте потребления , затраты на перевозку единицы продукта от пункта производства до пункта потребления . Предполагается, что суммарное производство равно суммарному потреблению: . Требуется составить план перевозок, позволяющий полностью вывезти продукты всех производителей, полностью обеспечивающий потребности всех потребителей и дающий минимум суммарных затрат на перевозку. Обозначим как объемы перевозок от поставщика до потребителя .

,

,

История поиска методов решения

Проблема была впервые формализована французским математиком Гаспаром Монжем в 1781 году . Прогресс в решении проблемы был достигнут во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем . Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.

Обобщения применения транспортной задачи

Транспортная задача в сетевой постановке

В этом варианте пункты не делятся на пункты отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление — отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты, включая производитель — производитель, потребитель — потребитель.

Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.

Транспортная задача с ограничениями пропускной способности

Вариант транспортной задачи в сетевой постановке, при котором задается максимальная пропускная способность некоторых дуг.

Задача решается слегка усложненным методом потенциалов.

Многопродуктовая транспортная задача

Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов). Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам).

Задача решается симплекс-методом (используется разложение Данцига — Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи).

Решение методом потенциалов

Транспортная задача решается методом потенциалов.

Решим задачу с перевозкой зерна. В качестве начального используем решение, полученное методом северо-западного угла.

В методе потенциалов каждой строке i и каждому столбцу j ставятся в соответствие числа, называемые потенциалами u_i и v_j. Для каждой базисной переменнойx_ij потенциалы должны удовлетворять уравненению:

u_i+v_j=c_ij

В нашей задаче 7 неизвестных переменных (потенциалов) и 6 уравнений, соответствующих базисным переменным. Одному из потенциалов присваивается произвольное значение (обычно полагают u₁=0), а затем последовательно вычисляют значения остальных потенциалов.

Итак, имеем : u₁=0, u₂=5, u₃=3

v₁=10, v₂=2, v₃=4, v₄=15.

Далее для каждой небазисной переменной вычисляются величины u_i+v_j-c_ij .

Небазисные переменные	Значения ui+vj-cij
x13	u1+v3-c13=0+4-20=-16
x14	u1+v4-c14=0+15-11=4
x21	u2+v1-c21=5+10-12=3
x31	u3+v1-c31=3+10-4=9
x32	u3+v2-c32=3+2-14=-9
x33	u3+v3-c33=3+4-16=-9

Поскольку ищется минимум стоимости перевозок, вводимой в базис будет переменная, имеющая наибольший положительный коэффициент.

В данном случае это будет x₃₁ (9).

Вычисления начинают с присвоения u₁=0. Об этом говорит сайт https://intellect.icu . Затем вычисляют v-потенциалы для всех столбцов, имеющих базисные переменные в первой строке. Далее на основании уравнения потенциалов, соответствующего x₂₂ определяется u₂. Зная u₂ вычисляем v₃ и v₄, и наконец u₃. Потенциалы определены, далее вычисляются величины u_i+v_j-c_ij для каждой небазисной переменной x_ij.

Определили вводимую в базис переменную x₃₁. Надо найти исключаемую.

Выбрав в качестве вводимой переменной x₃₁, мы хотим, чтобы перевозки по маршруты 3 – 1 уменьшили общую стоимость перевозок. Какой объем груза можно перевезти по этому маршруту ? Обозначим через количество груза перевозимого по маршруту (3,1), то есть x₃₁=. определим из условий:

1. Должны выполняться ограничения на спрос и предложение.

2. Ни по какому маршруту не должны выполняться перевозки с отрицательным объемом.

Построим цикл, который начинается и заканчивается в ячейке (3,1). Цикл состоит из последовательных горизонтальных и вертикальных отрезков, соединяющих ячейки, соответствующие текущим базисным переменным.

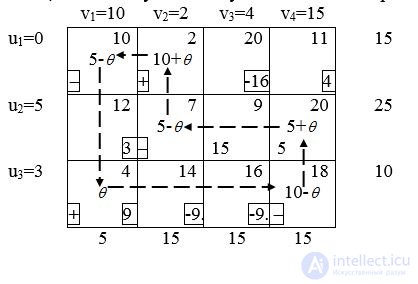
Найдем значение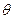 . Для того, чтобы удовлетворить ограничениям по спросу-предложению, надо поочередно отнимать и прибавлять 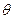к значениям переменных расположенных в угловых ячейках цикла. Новые значения базисных переменных останутся неотрицательными, если будут выполняться неравенства:

x₁₁=5-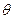≥0

x₂₂=5-≥0

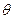x₃₄=10-≥0

Отсюда ясно, что наибольшее значение 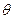=5. x₁₁ и x₂₂ при этом обращаются в нуль. Можно исключить как x₁₁, так и x₂₂. Исключим x₁₁ .

Итак x₃₁=5. Корректируем базовые переменные в угловых ячейках.

Стоимость перевозки единицы груза уменьшилась на u₃+v₁-c₃₁=9 долларов, суммарная стоимость на 95=45 долларов.

Повторяем вычисления потенциалов. Новой вводимой переменной будет x₁₄. Из цикла x₁₄=10, исключаемая переменная x₂₄.

Новое решение:

будет оптимально, так как u_i+v_j-c_ij для всех небазисных переменных отрицательно.

В терминах исходной задачи решение имеет смысл:

Двойственная задача к Т-задаче.

По общему правилу построения двойственных задач двойственная задача для транспортной запишется так:

при ограничениях:

u_i+v_i≤c_ij, ,

Смысл двойственных переменных:

u_i () – оценка единицы запаса (потенциал i-го поставщика);

v_j (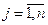) – оценка единицы спроса (потенциал j-го поставщика).

Задача о назначениях.

На практике часто необходимо решить следующие задачи: распределить рабочих по рабочим местам так, чтобы время изготовления продукта было минимальным, разместить датчики по объектам так, чтобы информация о работе объектов была максимальной, распределить экипажи самолетов по рейсам так, чтобы время простоя ЛА было минимальным и т.д.

Особенность этой задачи заключается в том, что каждый ресурс (рабочий, датчик, экипаж) используется ровно один раз и каждому объекту приписывается один ресурс.

Решение задачи представляется двумерным массивом или матрицей x_ij, i=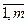 , j=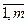, где m – число объектов или ресурсов. Искомая переменная

1, если i-й ресурс назначается на j-й объект,

x_ij=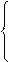

0,в противном случае.

Затраты, связанные с назначением i-го ресурса на j-й объект обозначают элементами матрицы стоимостей c_ij. Для любого нежелательного назначения соответствующую ему стоимость полагают равной достаточно большому числу M. Допустимое решение задачи называется назначением. Всего для матрицы размеромm×m существует m! решений. Допустимое решение строят путем выбора ровно одного элемента в каждой строке матрицы x_ij и ровно одного элемента в каждом ее столбце.

Таким образом, задача о назначениях формулируется так:

Z=

при ограничениях:

а) каждый ресурс используется ровно один раз: для всех i ;

б) каждому объекту приписан ровно один ресурс: для всех j.

Очевидно, что задача о назначениях является частным случаем транспортной задачи при единичных значениях параметров a_i и b_i. Для ее решения можно воспользоваться любым алгоритмом ЛП или методом потенциалов. Но с учетом ее специфики для ее решения применяют так называемый венгерский метод. Он впервые был предложен венгерским математиком Эгервари в 1931г. Долго его работа оставалась неизвестной. В 1953г. математик Г.Кун перевел работу Эгервари на английский язык, развил идеи Эгервари и назвал метод венгерским. Венгерский метод разрабатывался для ручных вычислений и сейчас представляет чисто исторический интерес.

Пример1. Разместить 3 датчика у 3-х объектов таким образом, чтобы стоимость такого размещения была минимальной. Матрица стоимости имеет вид:

Алгоритм венгерского метода.

Этап 1. В исходной матрице стоимостей определим в каждой строке минимальную стоимость и отнимем ее от других элементов строки.

Этап 2. В матрице, полученной на первом этапе, найдем в каждом столбце минимальную стоимость и отнимем ее от других элементов столбца.

Этап3. Оптимальным назначением будут соответствовать нулевые элементы полученные на этапе 2.

Обозначим через p_i и q_i минимальные стоимости в строке i и столбце j соответственно.

p₁=9, p₂=9 ,p₃=8

Вычтем p_i из элементов соответствующих строк.

q₁=0, q₂=2, q₃=0.

Выполним этап 2.

Подчеркнутые нули определяют оптимальное решение. Стоимость размещения равна 9+10+8=27 у.е. Отметим, что эта сумма всегда равна

(p₁+ p₂ +p₃) + ( q₁ +q₂ +q₃).

Иногда нельзя найти сразу допустимое решение и надо прибегнуть к дополнительным действиям.

Пример2.

p₁=1, p₂=7 , p₃=4, p₄=5

q₁=0, q₂=0, q₃=3, q₄=0

Нельзя для каждого датчика назначить 1 объект. Надо добавить к процедуре венгерского метода еще один этап.

Этап 2.1. Если после выполнения первого и второго этапов не получено допустимого решения, выполнить следующие действия:

1) В последней матрице провести минимальное число горизонтальных и вертикальных прямых, чтобы вычеркнуть в матрице все нулевые элементы.

2) Найти наименьший не вычеркнутый элемент и вычесть его из остальных не вычеркнутых элементов, а к элементам, стоящим на пересечении прямых – прибавить.

3) Если новое распределение не позволяет найти допустимое решение, повторить этап 2.1. В противном случае перейти к этапу 3.

Подчеркнут наименьший элемент.

Оптимальное решение подчеркнуто.

Z=1+10+5+5=21 у.е.

Обоснование венгерского метода основано на том, что если к каждому элементу i-й строки добавляют число γ_i (= - p_i), а к каждому элементу j-го столбца – действительное число δ_j (= - q_j), то минимизация функции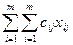 эквивалентна минимизации функции 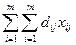, где d_ij=c_ij+γ_i+δ_i

Другие методы решения

Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей ее можно решить проще (для задач малой размерности).

Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из в груза , а в маленькие клетки — соответствующие тарифы .

Итерационное улучшение плана перевозок

Нахождение опорного плана

Требуется определить опорный план и путем последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.

Метод северо-западного угла (диагональный или улучшенный)

На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из или полностью удовлетворяется потребность .

Метод наименьшего элемента

Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.

Алгоритм:

1. Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.
2. Проверяются строки поставщиков на наличие строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.
3. Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.

Итерации

После нахождения опорного плана перевозок, нужно применить один из алгоритмов его улучшения, приближения к оптимальному.

• Метод падающего камня
• метод потенциалов .

Решение транспортной задачи с помощью теории графов

Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются ребрами бесконечной пропускной способности и цены за единицу потока .

К верхней доле искусственно присоединяется исток. Пропускная способность ребер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих ребер равна 0.

Аналогично к нижней доле присоединяется сток. Пропускная способность ребер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих ребер тоже равна 0.

Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Ее решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешевый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана — Форда. При возврате потока стоимость считается отрицательной.

Алгоритм «mincost maxflow» можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма «mincost maxflow» происходит не более чем за операций. ( — количество ребер, — количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка операций.

При решении несбалансированной транспортной задачи применяют прием, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Вау!! 😲 Ты еще не читал? Это зря!

• задача о назначениях ,
• метод мака ,
• транспортные задачи , задачи хичкока , т-задачи , метод форгеля ,
• Алгоритм аукциона
• Метрика Вассерштейна
• симплекс метод
• Метод северо-западного угла
• Метод наименьшего элемента
• алгоритм Форда-Фалкерсона
• алгоритм Беллмана -Форда
• Транспортная функция
• Венгерский алгоритм
• Планирование транспортировки
• Дистанция движителя земли (Расстояние копателя или ремонтника или расстояние Вассерштейна)

Надеюсь, эта статья об увлекательном мире алгоритм решения транспортной задачи, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое алгоритм решения транспортной задачи, транспортная задача, метод потенциалов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.