Лекция
Привет, сегодня поговорим про м-метод, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое м-метод, двухэтапный метод двойственность в линейном программировании , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
Два правила выбора вводимых и исключаемых переменных в симплекс-методе называются условием оптимальности и условием допустимости.
Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в Z-строке. Оптимальное решение будет достигнуто тогда, когда в Z-строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными).
Условие допустимости. Как в задаче минимизации, так и в задаче максимизации в качестве исключаемой выбирается базисная переменная, для которой положительное отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально.
Последовательность действий в симплекс-методе:
Этап 0. Находится начальное допустимое базисное решение.
Этап 1. На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются.
Этап 2. На основе условия допустимости выбираются исключаемая переменная.
Этап 3. Вычисляется новое базисное решение. Переход к п.1.
Искусственное начальное решение.
В примере Reddy Mikks при допустимом начальном базисном решении все последующие базисные решения, получаемы при выполнении симплекс-метода, также будут допустимыми. В задачах ЛП, где все ограничения есть неравенства типа «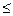 » (с неотрицательной правой частью) дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение. А как его сформировать, если есть неравенства типа «
» (с неотрицательной правой частью) дополнительные (остаточные) переменные позволяют сформировать начальное допустимое базисное решение. А как его сформировать, если есть неравенства типа « ». В этом случае используются искусственные переменные. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, а потом от них освобождаются. Разработано два метода нахождения начального решения с использованием искусственных переменных:
м-метод и двухэтапный метод.
». В этом случае используются искусственные переменные. Эти переменные в первой итерации играют роль дополнительных остаточных переменных, а потом от них освобождаются. Разработано два метода нахождения начального решения с использованием искусственных переменных:
м-метод и двухэтапный метод.
М-метод.
Пусть задача ЛП записана в стандартной форме. Для любого равенства, в котором не содержится дополнительная остаточная переменная, введем искусственную переменную R , которая далее войдет в начальное базисное решение. Но поскольку эта переменная искусственна (не имеет физического смысла в задаче), необходимо сделать так, чтобы на последующих итерациях она обратилась в нуль. Для этого в выражение целевой функции вводят штраф.
Переменная R, с помощью достаточно большого положительного числа М штрафуется путем введения в целевую функцию выражения –MR1,в случае максимизации и +MR1 - в случае минимизации. Вследствие этого штрафа резонно предположить, что процесс оптимизации приведет к нулевому значению R1.
Пример.
Минимизировать z=4x1+x2
3x1+x2=3
4x1+3x2 6
6
x1+2x2 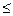 4
4
x1,x2 0
0
Приводим к стандартной форме:
z=4x1+x2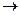 min
min
3x1+x2=3
4x1+3x2-x3=6
x1+2x2+x4= 4
x1,x2,x3,x4 0
0
Первое и второе уравнения не имеют дополнительных остаточных переменных, которые можно ввести в базисное решение. Поэтому введем в эти уравнения искусственные переменные R1 и R2, а в целевую функцию введем штраф MR1+MR2.
z=4x1+x2+ MR1+MR2
3x1+x2+R1 =3
4x1+3x2-x3+R2=6
x1+2x2+x4= 4
x1,x2,x3,x4,R1,R2 0
0
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
z |
-4 |
-1 |
0 |
-M |
-M |
0 |
0 |
|
R1 |
3 |
1 |
0 |
1 |
0 |
0 |
3 |
|
R2 |
4 |
3 |
-1 |
0 |
1 |
0 |
6 |
|
x4 |
1 |
2 |
0 |
0 |
0 |
1 |
4 |
Прежде чем применять симплекс-метод, надо согласовать Z-строку с остальной частью таблицы. Так Z, соответствующее начальному базисному решению R1=3,R2=6 и x4=4 должно равняться 3М+6М+0=9М, а не 0. Коэффициенты при R1 и R2 надо сделать нулевыми. Для этого надо строки R1 и R2 (все элементы) умножить на М, а затем сложить эти строки с Z-строкой.
Новая Z-строка = Старая Z-строка + M R1-строка + M
R1-строка + M R2-строка.
R2-строка.
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
z |
-4+7М |
-1+4М |
-М |
0 |
0 |
0 |
9М |
|
R1 |
3 |
1 |
0 |
1 |
0 |
0 |
3 |
|
R2 |
4 |
3 |
-1 |
0 |
1 |
0 |
6 |
|
x4 |
1 |
2 |
0 |
0 |
0 |
1 |
4 |
Теперь Z=9M, что соответствует базисному решению R1=3, R2=6 и x4=4.
Так как мы решаем задачу минимизации, выбираем наибольший положительный коэффициент в Z-строке. Об этом говорит сайт https://intellect.icu . Он равен -4+7М и соответствует переменной x1, которая будет вводимой. Условие допустимости указывает, что R1 – исключаемая.
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
z |
0 |
(1+5M)/3 |
-М |
(4-7M)/3 |
0 |
0 |
4+2M |
|
x1 |
1 |
1/3 |
0 |
1/3 |
0 |
0 |
1 |
|
R2 |
0 |
5/3 |
-1 |
-4/3 |
1 |
0 |
2 |
|
x4 |
0 |
3/5 |
0 |
-1/3 |
0 |
1 |
3 |
Уже первая итерация исключила из базисного решения R1 – это результат штрафа.
Следующими (вводимой и исключаемой переменной) будут x2 и R2 соответственно. И будет получено решение.
При использовании М-метода важны следующие обстоятельства:
1. Использование штрафа М может и не привести к исключению искусственной переменной. (Например, если система ограничений несовместна).
2. Теоретически применение М-метода требует, чтобы M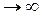 . Но с точки зрения компьютерных вычислений М должна быть конечной, но достаточно большой. Настолько большой, чтобы выполнять роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений.
. Но с точки зрения компьютерных вычислений М должна быть конечной, но достаточно большой. Настолько большой, чтобы выполнять роль «штрафа», но не слишком большой, чтобы не уменьшить точность вычислений.
Двухэтапный метод.
Он лишен недостатков, которые присущи М-методу вследствие ошибок округления. Процесс решения задачи разбивается на два этапа. На первом этапе ведется поиск допустимого решения. Если такое решение найдено, то на втором этапе решается исходная задача.
Этап 1. Задача ЛП записывается в стандартной форме, а в ограничения добавляются искусственные переменные , как и в М-методе. Решается задача ЛП минимизации суммы искусственных переменных с исходными ограничениями. Если минимальное значение этой новой целевой функции больше нуля, значит исходная задача не имеет допустимого решения и процесс вычислений заканчивается. Если новая целевая функция равна нулю, переходим ко второму этапу.
Этап 2. Оптимальное базисное решение, полученное на первом этапе, используется как начальное допустимое базисное решение исходной задачи.
Пример (та же задача)
Этап 1. Минимизировать z=R1+R2
3x1+x2+R1 =3
4x1+3x2-x3+R2=6
x1+2x2+x4= 4
x1,x2,x3,x4,R1,R2 0
0
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
r |
-4 |
-1 |
0 |
-1 |
-1 |
0 |
0 |
|
R1 |
3 |
1 |
0 |
1 |
0 |
0 |
3 |
|
R2 |
4 |
3 |
-1 |
0 |
1 |
0 |
6 |
|
x4 |
1 |
2 |
0 |
0 |
0 |
1 |
4 |
Как и в М-методе сначала вычисляется новая r-строка:
Новая r-строка = Старая r-строка + 1 R1-строка + 1
R1-строка + 1 R2-строка
R2-строка
Новая r-строка используется для решения задачи первого этапа.
|
Базис |
x1 |
x2 |
x3 |
R1 |
R2 |
x4 |
Решение |
|
r |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
|
x1 |
1 |
0 |
1/5 |
3/5 |
-1/5 |
0 |
3/5 |
|
x2 |
0 |
1 |
-3/5 |
-4/5 |
3/5 |
0 |
6/5 |
|
x4 |
0 |
0 |
1 |
1 |
-1 |
1 |
1 |
Достигнут минимум r=0, значит получено допустимое базисное решение x1=3/5,x2=6/5 и x4=1. Искусственные переменные выполнили свою миссию, и их можно удалить.
Далее выполняется Этап 2.
Двойственность в линейном программировании.
Каждой задаче ЛП можно поставить в соответствие так называемую двойственную задачу.
Задача ЛП в стандартной форме имеет вид:
Минимизировать или максимизировать
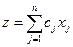
при ограничениях:
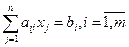
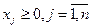
Правила формировании двойственной задачи:
1. Каждому из m ограничений прямой задачи соответствует переменная двойственной задачи
2.Каждой из n переменных прямой задачи соответствует ограничение
двойственной задачи.
3.Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничений двойственной задачи, соответствующей этой переменной, а правая часть формируемого ограничения равна коэффициенту при этой переменной в целевой функции.
4.Коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи.
В двойственной задаче меняется тип оптимизации целевой функции и тип ограничений.
Пример. Прямая задача
z=5x1+12x2+4x3 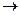 max
max
x1+2x2+x3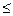 10
10
2x1-x2+3x3 = 8
x1,x2,x3 0
0
Прямая задача в стандартной форме:
z=5x1+12x2+4x3+0x4 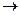 max
max
x1+2x2+x3+x4 = 10
2x1-x2+3x3+0x4 = 8
x1,x2,x3,x4  0
0
Двойственные переменные:
w=10y1+8y2 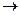 min
min
y1+2y2 5
5
2y1-y2  12
12
y1+3y2 4
4
y1+0y2 0
0
y1,y2 – свободные 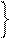 (y1
(y1 0, y2 – свободная переменная)
0, y2 – свободная переменная)
Пример. Прямая задача
z=15x1+12x2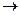 min
min
x1+2x2 3
3
2x1-4x2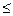 5
5
x1,x2  0
0
Прямая задача в стандартной форме:
z=15x1+12x2+0x3+0x4 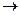 min
min
x1+2x2-x3+0x4 = 3
2x1-4x2+0x3+x4 = 5
x1,x2,x3,x4  0
0
Двойственные переменные: y1,y2
Двойственная задача:
w=3y1+5y2 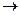 max
max
y1+2y2 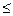 15
15
2y1-4y2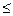 12
12
-y1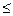 0 (или y1
0 (или y1 0)
0)
y2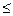 0
0
y1,y2-свободные переменные.
Смысл двойственной задачи.
Пусть задана задача оптимального распределения ресурсов. Ресурсы b1,b2..bm могут использоваться для выпуска n видов продукции. Известны стоимость j-го вида продукта cj (j=) и норма потребления i-го ресурса (i=) на производство единицы продукта j – aij. Требуется определить объем производства продукта каждого вида xj (j=), максимизирующий доход
z=c1x1+c2x2+..+cnxn
Расход ресурсов не должен превышать их наличия:
a11x1+a12x2+..+a1nxnb1
------------------------------------------
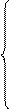 ai1x1+ai2x2+..+ainxnbi
ai1x1+ai2x2+..+ainxnbi
------------------------------------------
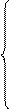 am1x1+am2x2+..+amnxnbm
am1x1+am2x2+..+amnxnbm
Все переменные неотрицательны.
Допустим, что вместо производства можно продавать сырье другому покупателю. Спрашивается, какую минимальную цену надо установить за единицу каждого вида сырья (i=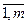 ) при условии, что доход от реализации всех его запасов должен быть не меньше того, который можно получить при выпуске продуктов из этого сырья. Учет интересов покупателя связан с минимизацией суммарной стоимости сырья. Ответ на этот вопрос дает двойственная задача.
) при условии, что доход от реализации всех его запасов должен быть не меньше того, который можно получить при выпуске продуктов из этого сырья. Учет интересов покупателя связан с минимизацией суммарной стоимости сырья. Ответ на этот вопрос дает двойственная задача.
w=b1y1+b2y2+..+bmym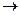 min
min
a11y1+a21y2+..+am1ymc1
------------------------------------------
a1jy1+a2jy2+..+amjymcj
------------------------------------------
a1ny1+a2ny2+..+amnymcn
yi 0, (i=
0, (i=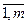 )
)
Переменные yi двойственной задачи отражают «ценность» i-го ресурса. В связи с этим переменные двойственной задачи называют теневыми ценами или скрытыми доходами (иногда симплексными мультипликаторами).
Двойственной к двойственной задаче является прямая. В системе «прямая - двойственная» обе задачи являются равноценными. Любую из них можно рассматривать как прямую, тогда вторая будет двойственной ей.
Основные теоремы двойственности.
Теорема 1. Если x0 и y0 – допустимые решения прямой и двойственной задач, т.е. Ax0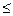 b и ATy0
b и ATy0 c, то
c, то
cTx0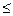 bTy0,
bTy0,
т.е. значения целевой функции прямой задачи никогда не превышают значений целевой функции двойственной задачи.
Теорема 2 (основная теорема двойственности). Если x0 и y0 – допустимые решения прямой и двойственной задач и если cTx0=bTy0, то x0 и y0 – оптимальные решения пары двойственных задач.
Именно эта теорема связывает оптимальные решения прямой и двойственной задач. Если в прямой задаче при малом количестве переменных имеется большое количество ограничений (m>n), выгоднее решать двойственную задачу.
Теорема 3. Если в оптимальном решении прямой задачи i-е ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю.
Смысл таков : Если некоторый ресурс bi имеется в избытке и i-е неравенство выполняется как строгое неравенство, то оно становится несущественным и оптимальная теневая цена такого ресурса равна нулю.
Теорема 4. Если в оптимальном решении двойственной задачи ограничение j выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю.
Дадим интерпретацию теоремы 4. Поскольку величины yi(i=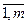 )- это цены соответствующих ресурсов, то
)- это цены соответствующих ресурсов, то 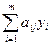 - это затраты на j-й технологический процесс. Теорема тогда означает следующее: если j-й технологический процесс оказывается невыгодным с точки зрения оптимальных цен ресурсов yопт, то в оптимальном решении прямой задачи интенсивность такого технологического процесса должна быть равна нулю. Теорема 4 выражает принцип рентабельности оптимально функционирующей системы.
- это затраты на j-й технологический процесс. Теорема тогда означает следующее: если j-й технологический процесс оказывается невыгодным с точки зрения оптимальных цен ресурсов yопт, то в оптимальном решении прямой задачи интенсивность такого технологического процесса должна быть равна нулю. Теорема 4 выражает принцип рентабельности оптимально функционирующей системы.
Решение задачи ЛП путем графического анализа двойственности.
z=-6x1-12x2+3x3-x4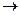 max
max
 2x1-4x2+3x3-x4=6
2x1-4x2+3x3-x4=6
-3x1+3x2+x3=12
Двойственная задача:
w=6u1+12u2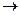 min
min
2u1-3u2 -6
-6
-4u1+3u2 -12
-12
3u1+u2 3
3
-u1 -1
-1
u1,u2 –свободные

Область допустимых решений - 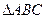 . Оптимальное решение достигается в т.C(1,0) и wmin=6. Этим решением удовлетворяются как строгие равенства первое и второе ограничения (2-0=2>-6 и -4+0=-4>-12). Соответствующие им переменные прямой задачи равны нулю. Тогда
. Оптимальное решение достигается в т.C(1,0) и wmin=6. Этим решением удовлетворяются как строгие равенства первое и второе ограничения (2-0=2>-6 и -4+0=-4>-12). Соответствующие им переменные прямой задачи равны нулю. Тогда
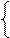 3x3-x4=6
3x3-x4=6
x3=12
Отсюда x3=12, x4=30. Решение прямой задачи x0=(0,0,12,30). zmax=3 12-1
12-1 30=6. Так как zmax=wmin=6, то вычисления выполнены верно.
30=6. Так как zmax=wmin=6, то вычисления выполнены верно.
Надеюсь, эта статья об увлекательном мире м-метод, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое м-метод, двухэтапный метод двойственность в линейном программировании и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.