Элемент вероятности в теории игр кратко

Привет, мой друг, тебе интересно узнать все про элемент вероятности в теории игр, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое элемент вероятности в теории игр , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

В реальной жизни происходит много непредсказуемых внешних событий, из-за которых люди попадают в непредвиденные ситуации. Эта непредсказуемость отражается во многих играх за счет включения элемента случайности, такого как метание жребия. Таким образом, игры с элементов случайности позволяют нам на один шаг приблизиться к реальности и поэтому имеет смысл рассмотреть, как это отражается на процессе принятия решений.

Одной из типичных игр, в которых сочетается удача и искусство, являются нарды. Перед каждым своим ходом игрок бросает кубики для определения допустимых ходов. Например, в позиции игры в нарды, приведенной на рисунке, белым выпали очки 6-5 и они имеют четыре возможных хода.

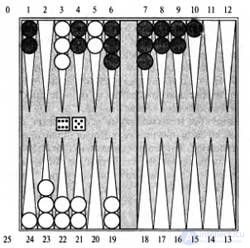
Типичная позиция игры в нарды. Цель игры состоит в том, чтобы снять с доски все фишки. Белые ходят по часовой стрелке к полю 25, а черные — против часовой стрелки к полю 0. Фишка может переходить на любое поле, если на нем не находится несколько фишек противника; если же на этом поле есть только одна фишка противника, она попадает в плен и должна начать свое движение с самого начала. В показанной здесь позиции белые после метания жребия получили очки 6-5 и должны выбирать среди четырех допустимых ходов: (5-10,5-11), (5-11,19-24), (5-10,10-16) и (5-11,11-16)

Хотя белым известно, каковы их допустимые ходы, они не знают, какие очки принесет метание жребия черным, и поэтому не могут определить, какими будут допустимые ходы черных. Об этом говорит сайт https://intellect.icu . Это означает, что белые не имеют возможности сформировать стандартное дерево игры такого типа, которое встретилось нам в шахматах, а также крестиках-ноликах. Дерево игры в нарды, кроме узлов МАХ и MIN, должно включать узлы жеребьевки. Узлы жеребьевки обозначены на рисунке кружками.

Ветви, ведущие от каждого узла жеребьевки, обозначают возможные результаты метания жребия, поэтому каждая из них отмечена надписью с указанием количества очков и вероятности, с которой могут быть получены эти очки. Существуют 36 различных сочетаний очков на двух кубиках, и все они являются равновероятными; но поскольку такие сочетания очков, как 6-5 и 5-6, являются одинаковыми, имеется только 21 различимое сочетание очков. Вероятность появления шести дублей (от 1-1 до 6-6) равна 1/36, а каждое из 15 остальных различных сочетаний очков имеет вероятность 1/18.

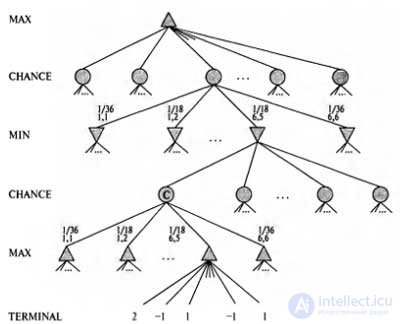Схематическое изображение дерева игры для одной из позиций игры в нарды

Следующий этап состоит в том, чтобы понять, как следует принимать правильные решения. Безусловно, и в этом случае требуется найти такой ход, который ведет к наилучшей позиции. Однако результирующие позиции не имеют определенных минимаксных значений. Вместо этого существует возможность вычислить только ожидаемое значение, в котором ожидаемый результат устанавливается с учетом всех возможных выпадений жребия, которые могут произойти. Это приводит к обобщению минимаксного значения для детерминированных игр до ожидаемого минимаксного значения (expectiminimax value) для игр с узлами жеребьевки.

Терминальные узлы и узлы мах и MIN (для которых известны результаты жеребьевки) применяются точно так же, как и прежде, а узлы жеребьевки оцениваются путем получения взвешенного среднего значений, полученных в результате всех возможных выпадений жребия, т.е. следующим образом:

где функция определения преемника доя узла жеребьевки n просто дополняет состояние n каждым возможным выпадением жребия для формирования каждого преемника s, а P(s) — вероятность, с которой происходит выпадение жребия. Результаты вычисления этих уравнений могут резервироваться рекурсивно во всех узлах вплоть до корня дерева точно так же, как и в минимаксном алгоритме. Оставляем читателю проработку всех деталей этого алгоритма в качестве упражнения.

Если я не полностью рассказал про элемент вероятности в теории игр? Напиши в комментариях Надеюсь, что теперь ты понял что такое элемент вероятности в теории игр и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.