Лекция
Привет, Вы узнаете о том , что такое метод мака, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод мака , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
При решении некоторых задач менеджмента необходимо назначать исполнителей (людей, механизмы и т.п.) для выполнения однотипных работ. метод мака применяется для распределения функций между элементами системы, когда каждый из этих элементов способен выполнять любую из функций с разной эффективностью [1, с. 240]. Предполагается выполнение одним элементом одной функции, и на выходе системы необходимо получить максимальную эффективность. К примеру, в организации n работников, между которыми требуется распределить n заданий так, чтобы все задания были выполнены за суммарно минимальное время. Время выполнения заданий напрямую зависит от свойств характера исполнителей, их квалификации. Следовательно, эффективность труда исполнителей, в силу этих и иных причин, будет различна.
Данная задача носит название задачи о назначениях и представляет собой частный случай более общей транспортной задачи. Существует определенный алгоритм решения задачи о назначениях методом Мака. В первую очередь, составляется матрица: допустим, по вертикали указываются номера работников (Р) организации, а по горизонтали - номера заданий (З), которые соответствуют разным должностям. Таблицу заполняем значениями времени выполнения заданий. Требуется найти минимальное суммарное время выполнения всех n заданий. Ниже приведен пример таблицы исходных данных.

Далее необходимо составить систему ограничений по строкам и столбцам. Так как каждый работник должен быть задействован и выполнять одно задание, которое, в свою очередь, должно быть выполнено, сумма элементов в каждой строке (так же и со столбцами) должна быть равна 1 [2, с. 97].
Полное время выполнения заданий будет являться целевой минимизируемой функцией, где в качестве коэффициентов при Х_у будут выступать соответствующие значения времен.
В основе методики решения данной задачи методом Мака лежит принцип, заключающийся в том, что положения оптимального выбора не меняются, если к каждому элементу какой-либо строки или столбца добавить одно и то же число или вычесть его [3, с. 148].
Задача о назначениях – одна из наиболее известных дискретных оптимизационных задач. Цель задачи — найти оптимальное (минимальной стоимости) распределение работников по заданным работам. Задача о назначениях имеет широкое применение, например, при закреплении машин за маршрутами, распределении инструментов для обработки различных марок стали и т.д.
Постановка задачи.

Очевидный метод решения задачи заключается в переборе n! перестановок. Однако на практике такой неэффективный способ становится неприменимым уже для матриц небольших размеров.
Задача о назначениях является частным случаем общих классов оптимизационных задач, и поэтому существует много разнообразных методов ее решения.
Разделить множество столбцов на А и A', где
А – выбранное множество,
A' – невыбранное
В начале вычислений и при переходе от циклов к началу выбранных столбцов нет; все столбцы относятся к A'.
Выбрать из множества A' столбец, содержащий более одного подчеркнутого элемента, перевести этот столбец изA' в А.
Подчеркнутый элемент – минимальный элемент в строке.
Примечание: перед первым шагом алгоритма множество А всегда является пустым.
Если подчеркнутый элемент находится в множестве А, найти в каждой строке разность между минимальным подчеркнутым и минимальным неподчеркнутым элементами. Об этом говорит сайт https://intellect.icu . Из всех найденных разностей выбрать минимальную.
Увеличить все элементы матрицы А на выбранную на 2-м шаге минимальную разность.
В строке с минимальной разностью отметить пунктиром минимальный неподчеркнутый элемент 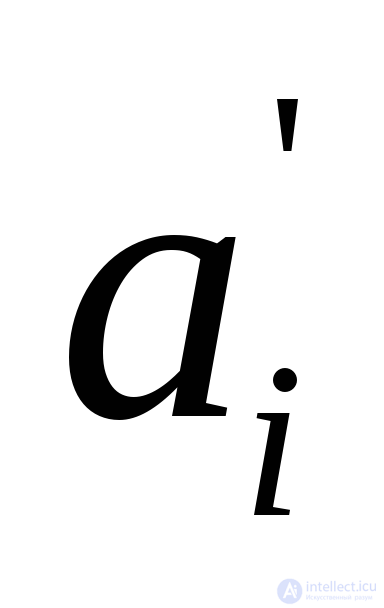
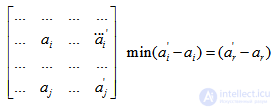
Столбец, содержащий отмеченный пунктиром элемент 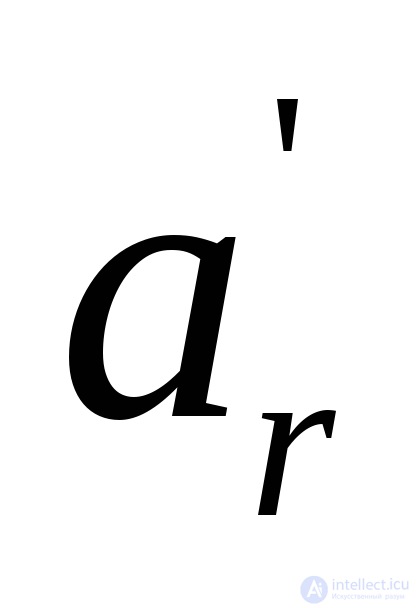 , перенести в множество С.
, перенести в множество С.
Если в С более 2-х неподчеркнутых элементов, то перенести С из A' в А и перейти ко 2-му шагу. Иначе, перейти к 6-му шагу.
Отмеченный пунктиром элемент 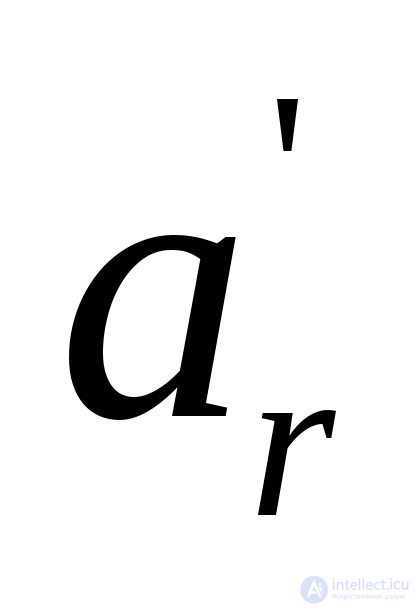 подчеркнуть (
подчеркнуть (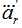 меняется на
меняется на 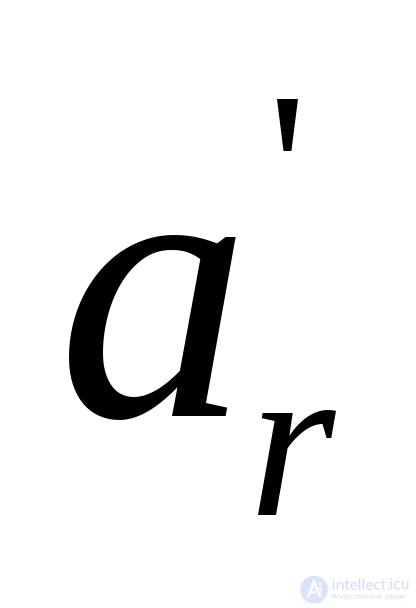 ).
).
Найти исходный подчеркнутый элемент в строке с минимальной разностью (в той строке, где 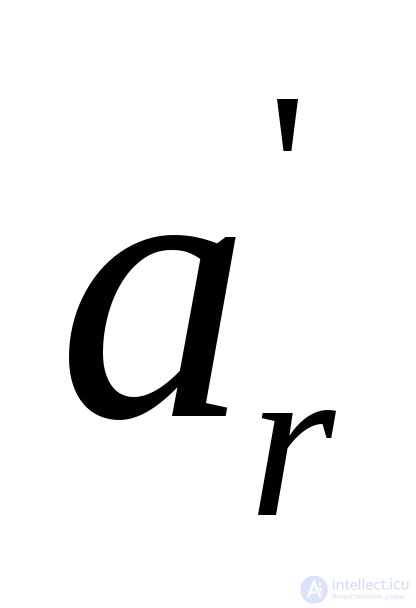 ) и убрать подчеркивание (
) и убрать подчеркивание (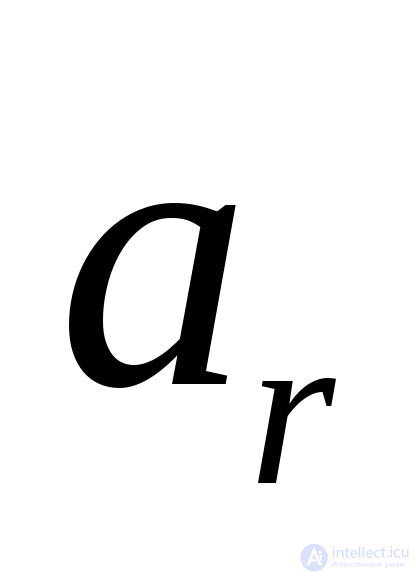 меняется на
меняется на ). Обозначить столбец с элементом
). Обозначить столбец с элементом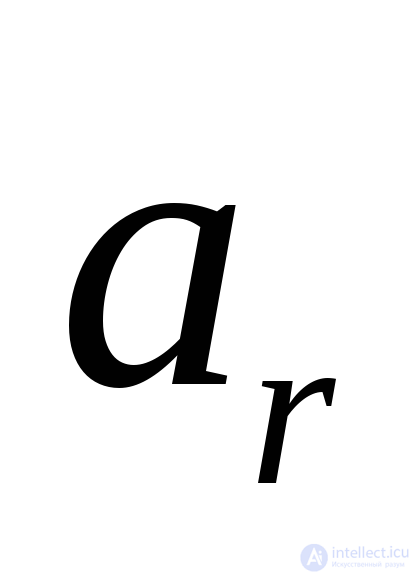 D.
D.
Если Dне содержит других подчеркнутых элементов, он должен содержать элементы, отмеченные пунктиром. Обозначить этот элемент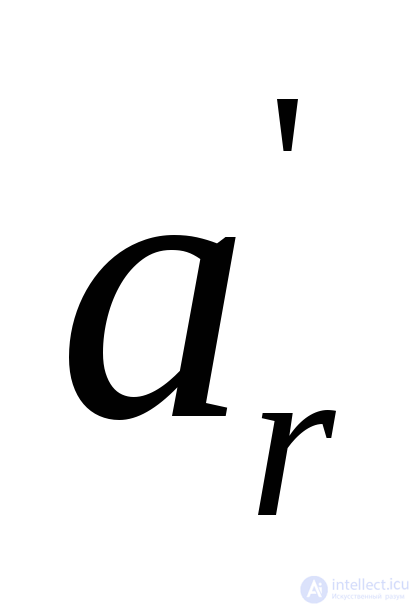 и перейти к 6-му шагу.
и перейти к 6-му шагу.
Если Dсодержит еще 1 подчеркнутый элемент, то полностью подчеркнутые элементы образуют новый базис. В этом случае перейти к 1-му шагу.
Пример 4.Исходная таблица:

Подчеркнем минимальные элементы в строке и внесем в множество А первый столбец, т.к. в нем два подчеркнутых элемента. Минимальная разность из найденных соответствует второй строке. Поскольку эта разность равна 0, элементы множества А остаются без изменений. Перейдем к следующей таблице.
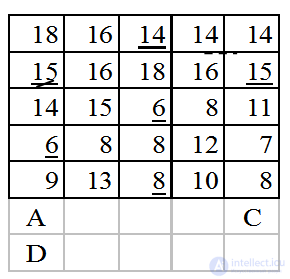

Отметим пунктиром элемент  . Добавим пятый столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента
. Добавим пятый столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента и обозначаем первый столбец буквойD. ВDесть еще один подчеркнутый элемент
и обозначаем первый столбец буквойD. ВDесть еще один подчеркнутый элемент , значит, переходим к первому шагу.
, значит, переходим к первому шагу.
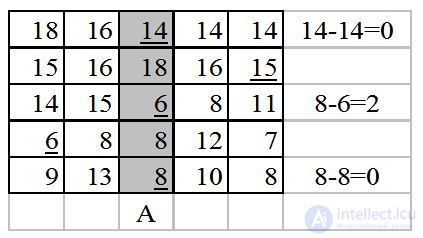
Внесем в множество А третий столбец, найдем минимальную разность и перейдем к следующей таблице.
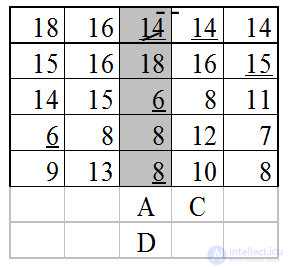

Отметим пунктиром элемент  . Добавим четвертый столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента
. Добавим четвертый столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента и обозначаем третий столбец буквойD. ВDесть еще подчеркнутые элементы, значит, переходим к первому шагу.
и обозначаем третий столбец буквойD. ВDесть еще подчеркнутые элементы, значит, переходим к первому шагу.
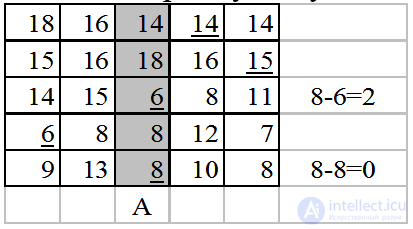
Внесем в множество А третий столбец, найдем минимальную разность и перейдем к следующей таблице.
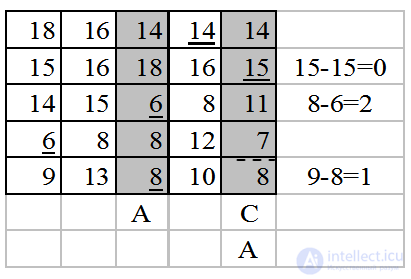
Отметим пунктиром элемент  . Добавим пятый столбец в множество С. В С есть еще подчеркнутые элементы, поэтому переводим пятый столбец в А. Минимальная разность соответствует второй строке.
. Добавим пятый столбец в множество С. В С есть еще подчеркнутые элементы, поэтому переводим пятый столбец в А. Минимальная разность соответствует второй строке.

Отметим пунктиром элемент 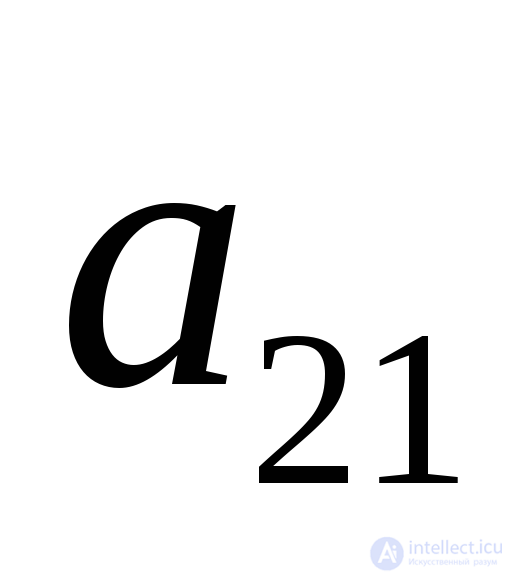 . Добавим первый столбец в множество С. В С есть еще подчеркнутые элементы, поэтому переводим пятый столбец в А. Минимальная разность соответствует второй строке. Прибавляем ко всем элементам множества А величину минимальной разности, т.е. 1.
. Добавим первый столбец в множество С. В С есть еще подчеркнутые элементы, поэтому переводим пятый столбец в А. Минимальная разность соответствует второй строке. Прибавляем ко всем элементам множества А величину минимальной разности, т.е. 1.
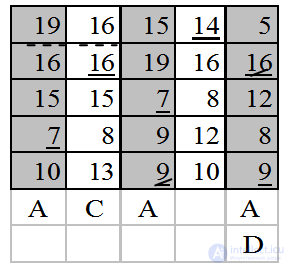
Отметим пунктиром элемент  . Добавим второй столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента
. Добавим второй столбец в множество С. В С только один подчеркнутый элемент. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента и обозначаем пятый столбец буквойD. ВDесть один подчеркнутый пунктиром элемент
и обозначаем пятый столбец буквойD. ВDесть один подчеркнутый пунктиром элемент . Подчеркиваем его сплошной чертой, убираем подчеркивание элемента
. Подчеркиваем его сплошной чертой, убираем подчеркивание элемента . Распределение закончено.
. Распределение закончено.
Соответствующее значение целевой функции:
f= 6 + 16 + 6 + 14 + 8 = 50
Исследование, описанное в статье про метод мака, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое метод мака и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Из статьи мы узнали кратко, но содержательно про метод мака
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.