Лекция
Привет, Вы узнаете о том , что такое упаковка кругов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое упаковка кругов , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
В геометрии упаковка кругов — это изучение размещения кругов (одного размера или разных размеров) на заданной поверхности таким образом, что они не пересекаются и круги касаются друг друга. Соответствующая плотность упаковки η размещения — это доля занятой кругами поверхности. Можно обобщить упаковки кругов на более высокие размерности — она называется упаковкой шаров, которая, обычно, работает с одинаковыми сферами.
В то время как окружности имеют относительно низкую максимальную плотность упаковки 0.9069 на евклидовой плоскости, эта плотность не минимальна. «Худшая» фигура упаковки плоскости не известна, хотя сглаженный восьмиугольник имеет плотность упаковки около 0.902414, что является наименьшей максимальной плотностью упаковки, известной для центрально-симметричных выпуклых фигур . Плотность упаковки вогнутых фигур, таких как звездчатые многоугольники, может быть произвольно малой.
Ветвь математики, известная как «упаковка кругов», занимается геометрией и комбинаторикой упаковок кругов произвольного размера и из нее подымаются дискретные аналоги конформных отображений, римановых поверхностей и им подобные.
Для двумерного евклидова пространства Жозеф Луи Лагранж доказал в 1773, что решетчатая упаковка кругов высшей плотности — это шестиугольная упаковка , в которой центры кругов располагаются на шестиугольной решетке (расположенные зигзагом ряды, подобные сотам), а каждый круг окружен шестью другими окружностями. Плотность такой упаковки равна
Аксель Туэ привел первое доказательство, что эта упаковка оптимальна в 1890, показав,что шестиугольная решетка является самой плотной из всех возможных упаковок кругов, как регулярных, так и нерегулярных. Однако это доказательство считалось не вполне полным. Первое полноценное доказательство приписывается Ласло Фейеш Тоту (1940) .
С другой стороны, были обнаружены жесткие упаковки кругов низкой плотности.
Существует 11 упаковок кругов на основе 11 однородных мозаик плоскости . В этих упаковках любая окружность может быть отображена на любую другую окружность путем отражения или вращения. Шестиугольные промежутки могут быть заполнены одним кругом, а двенадцатиугольные промежутки могут быть заполнены 7 кругами, образуя 3-однородные упаковки. Усеченная тришестиугольная мозаика с обоими типами промежутков могут быть заполнена как 4-однородная упаковка. Плосконосая тришестиугольная мозаика имеет две зеркальные формы.
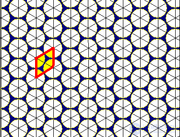 Треугольная |
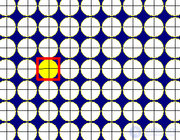 Квадратная |
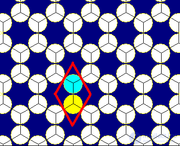 Шестиугольная |
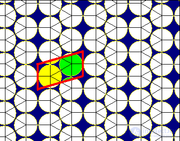 Удлиненная треугольная |
 Тришестиугольная |
 Плосконосая квадратная |
 Усеченная квадратная |
 Усеченная шестиугольная |
 Ромботришестиугольная |
 Плосконосая шестиугольная |
 Плосконосая шестиугольная (зеркальная) |
 Усеченная тришестиугольная |
Связанная задача — определение расположения с минимальной энергией одинаково расположенных точек, которые должны лежать на заданной поверхности. Задача Томсона рассматривает распределение электрических зарядов с наименьшей энергией на поверхности сферы. Задача Таммеса является обобщением этой задачи и максимизирует минимальное расстояние между кругами на сфере.
Упаковка кругов в простых ограниченных фигурах является общим типом задач занимательной математики. Об этом говорит сайт https://intellect.icu . Влияние стен контейнера важно, и шестиугольная упаковка в общем случае не является оптимальной для малого числа кругов.
Существует также ряд задач, которые разрешают размеры кругов быть неоднородными. Одним из таких расширений является задача нахождения максимально возможной плотности системы с двумя размерами кругов (бинарная система). Только девять определенных отношений радиусов позволяют компактную упаковку, в которой, если две окружности касаются, они вместе касаются также еще двух кругов (если соединить отрезками центры касающихся окружностей, они триангулируют поверхность) . Для семи таких отношений радиусов известны компактные упаковки, на которых достигается максимальное возможное отношение упаковки (выше, чем для кругов одного диаметра) для смеси кругов данного отношения радиусов. Высшая плотность упаковки — 0.911627478 для отношения радиусов 0.545151042 .
Также известно, что если отношение радиусов выше 0.742, бинарная смесь не может быть упакована лучше, чем круги одного размера . Верхние границы, которые могут быть достигнуты такой бинарной упаковкой для меньших отношений радиусов, также получены.
Квадратурная амплитудная модуляция основана на упаковке кругов в круги фазовоамплитудного пространства. Модем передает данные как серии точек на 2-мерной фазовоамплитудной плоскости. Расстояния между точками определяет восприимчивость шума при передаче, в то время как диаметр внешней окружности определяет требуемую мощность передатчика. Производительность максимальна, когда сигнальное созвездие кодовых точек находится в центрах плотной упаковки окружностей. На практике часто применяется прямоугольная упаковка для упрощения декодирования.
Упаковка окружностей стала существенным средством в искусстве оригами, так как каждая часть в фигуре оригами требует круг на листе бумаге . Роберт Лэнг использовал математику упаковки кругов для разработки компьютерных программ, предназначенных для разработки сложных фигур оригами.
Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг.
История
Эта задача упаковки была поставлена и исследовалась в 60-х годах 20-го века. Кравиц в 1967 опубликовал упаковки до 19 кругов без анализа оптимальности решений . Годом позже Грэм доказал, что найденные решения с числом кругов до 7 оптимальны , а Перл (Pirl), независимо от него, что оптимальны упаковки до 10 кругов. Лишь в 1994 Мелиссеном (Melissen) была доказана оптимальность решения с 11 кругами . Фодор (Fodor) показал между 1999 и 2003 годами, что решения с 12 , 13 и 19 кругами оптимальны.
Грэм (Graham) и др. около 1998 предложили два алгоритма и нашли с помощью них упаковки до 65 кругов . Последний обзор задачи и приближенных решений до 2989 кругов (июнь 2014) дал Экард Спехт (Eckard Specht)
Минимальные решения (в случае существования нескольких минимальных решений показан только один вариант):
| Число единичных кругов | Радиус вмещающей окружности | Плотность | Оптимальность | Диаграмма |
|---|---|---|---|---|
| 1 | 1 | 1.0000 | Тривиально оптимальна. |  |
| 2 | 2 | 0.5000 | Тривиально оптимальна. |  |
| 3 | 1+233 |
0.6466... | Тривиально оптимальна. |  |
| 4 | 1+2 |
0.6864... | Тривиально оптимальна. |  |
| 5 | 0.6854... | Тривиально оптимальна. Доказана оптимальность также Грэмом в 1968 |  |
|
| 6 | 3 | 0.6667... | Тривиально оптимальна. Доказана оптимальность также Грэмом в 1968 |  |
| 7 | 3 | 0.7778... | Тривиально оптимальна. |  |
| 8 | 0.7328... | Доказана оптимальность Перлом (Pirl) в 1969 |  |
|
| 9 | 0.6895... | Доказана оптимальность Перлом (Pirl) в 1969 |  |
|
| 10 | 3.813... | 0.6878... | Доказана оптимальность Перлом (Pirl) в 1969 |  |
| 11 | 0.7148... | Доказана оптимальность Мелиссеном (Melissen) в 1994 |  |
|
| 12 | 4.029... | 0.7392... | Доказана оптимальность Фодором (Fodor) в 2000 |  |
| 13 | 2+5 |
0.7245... | Доказана оптимальность Фодором (Fodor) в 2003 |   |
| 14 | 4.328... | 0.7474... | Гипотетически оптимальна |  |
| 15 | 1+6+25+41+25 |
0.7339... | Гипотетически оптимальна |  |
| 16 | 4.615... | 0.7512... | Гипотетически оптимальна |  |
| 17 | 4.792... | 0.7403... | Гипотетически оптимальна |  |
| 18 | 1+2+6 |
0.7611... | Гипотетически оптимальна |  |
| 19 | 1+2+6 |
0.8034... | Доказана оптимальность Фодором (Fodor) в 1999 |  |
| 20 | 5.122... | 0.7623... | Гипотетически оптимальна |  |
Гипотеза Пала Эрдеша и Нормана Олера утверждает, что в случае, когда n является треугольным числом, оптимальная упаковка n − 1 и n кругов имеет одну и ту же длину стороны. То есть, согласно гипотезе, оптимальное решение для n − 1 кругов можно получить путем удаление одного круга из оптимальной шестиугольной упаковки n кругов .
Минимальные по длине стороны треугольника решения :
| Число кругов | Длина стороны треугольника |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | 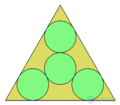 |
| 5 |   |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 |
Близкая задача — покрытие правильного треугольника заданным числом кругов с как можно меньшим радиусом .
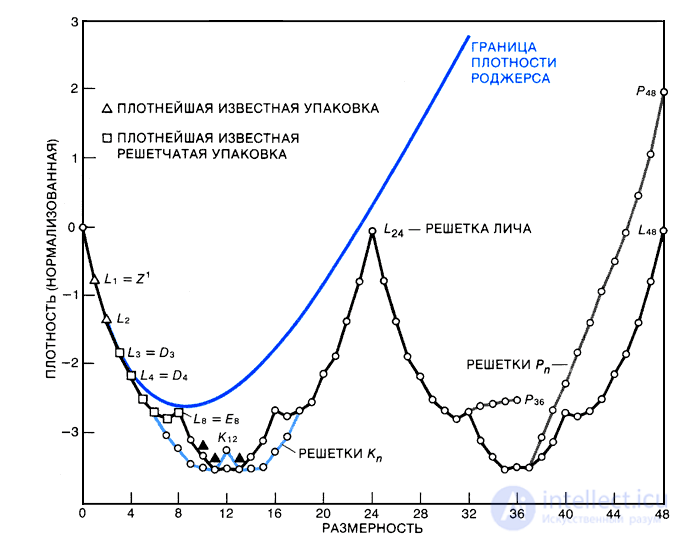
Рис. 9. Самые плотные известные упаковки шаров в пространствах вплоть до размерности 48 изображены на этом графике, построенном по методу, предложенному Джоном Личем; показана зависимость «нормализованной» плотности упаковки от размерности пространства. Определение нормализованной плотности основано на том факте, что отношение плотности 24-мерной решетки Лича к объему 24-мерного шара единичного радиуса равно 1. (Объем n-мерного шара радиуса 1 равен

Исследование, описанное в статье про упаковка кругов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое упаковка кругов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.