Лекция
Привет, Вы узнаете о том , что такое задача о назначениях, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое задача о назначениях , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
задача о назначениях — одна из фундаментальных задач комбинаторной оптимизации в области математической оптимизации или исследовании операций. Задача состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.
В наиболее общей форме задача формулируется следующим образом:
Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.
Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют в виду линейную задачу о назначениях.
В самом общем виде задача выглядит следующим образом:
Экземпляр задачи имеет ряд агентов и ряд задач . Любому агенту может быть назначено выполнение любой задачи, что требует определенных затрат , которые могут варьироваться в зависимости от назначения задачи агента. Требуется выполнить как можно больше задач, назначив не более одного агента на каждую задачу и не более одной задачи на каждого агента таким образом, чтобы общая стоимость назначения была минимальна.

Рабочий пример назначения задач неравному количеству работников по венгерскому методу
В качестве альтернативы, описывая задачу с помощью теории графов:
Задача о назначениях состоит в том, чтобы найти во взвешенном двудольном графе паросочетание заданного размера , в котором сумма весов ребер минимальна.
Если числа агентов и задач равны, то задача называется сбалансированным назначением . В противном случае это называется несбалансированным назначением . Если общая стоимость задания по всем задачам равна сумме затрат по каждому агенту (или сумме затрат по каждой задаче, что в данном случае одно и то же), то задача называется линейное задание . Обычно, когда говорят о задаче о назначениях без каких-либо дополнительных уточнений, имеют в виду линейную сбалансированную задачу о назначениях .
Венгерский алгоритм — один из многих алгоритмов, разработанный для решения линейной задачи о назначениях за полиномиальное время от числа работ.
Задача о назначениях является частным случаем транспортной задачи, которая является частным случаем задачи нахождения потока минимальной стоимости, а она, в свою очередь, является частным случаем задачи линейного программирования. Любую из этих задач можно решить симплекс-методом, но каждая специализация имеет свой более эффективный алгоритм, опирающийся на особенности структуры задачи.
Если целевая функция выражается через квадраты, говорят о квадратичной задаче о назначениях.
Предположим, что таксомоторная компания имеет три свободные машины (исполнители), и три заказчика (работы), желающих получить такси как можно быстрее. Об этом говорит сайт https://intellect.icu . Фирма заботится о времени доставки такси к заказчику, так что для каждой машины стоимость определяется временем, с которым машина доберется до места ожидания, определенного заказчиком. Решением задачи о назначениях будет распределение машин по заказчикам такое, что суммарная стоимость (суммарное время ожидания) минимальна.
Задачу о назначениях можно сделать более гибкой. В вышеприведенном примере могут оказаться не три, а четыре свободных такси, но заказчика по-прежнему три. Можно назначить четвертого фиктивного заказчика с нулевой стоимостью, распределение же машины на фиктивного заказчика означает — «ничего не делай».
Аналогичный прием можно использовать в случае, когда число заказов может превышать число доступных машин, и машина может быть назначена на выполнение нескольких работ, а также когда работа может быть назначена нескольким исполнителям (например, если заказчик — группа, не помещающаяся в одно такси). Можно также поставить задачу увеличения дохода, а не минимизацию цены.
Формальная постановка задачи о назначениях:
Даны два множества A и T одного размера и задана функция стоимости C : A × T → R.
Необходимо найти биекцию f : A → T такую, что целевая функция:
минимальна.
Обычно функция стоимости задается как квадратная матрица C, состоящая из вещественных чисел так, что целевую функцию можно записать в виде:
Задача называется «линейной», поскольку и целевая функция, и ограничения содержат только линейные выражения.
Задачу можно представить как задачу линейного программирования c целевой функцией
и ограничениями
для
,
для
,
для
.
Переменная представляет назначение исполнителя
на работу
, принимая значение 1 если исполнитель назначен на эту работу и 0 в противном случае. В этой формулировке решение может и не быть целым, но всегда существует оптимальное решение с целыми значениями. Этот факт следует из абсолютной унимодулярности матрицы. Первое ограничение требует, чтобы каждому исполнителю была назначена в точности одна задача, второе требует, чтобы для каждой задачи был назначен один исполнитель.
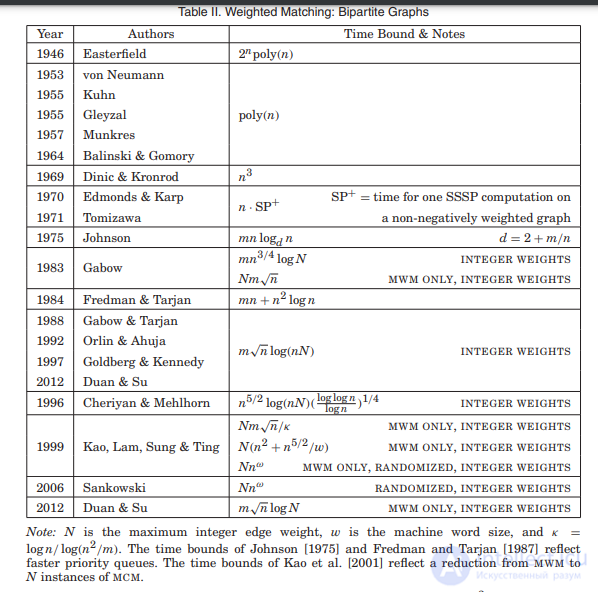
Существуют и другие подходы к проблеме назначения, которые были рассмотрены Дуаном и Петти (см. Таблицу II). В их работе встречается алгоритм аппроксимации задачи (и более общей задачи высокого веса ), который увеличивается за линейное время для любой фиксированной границы ошибки.
Обобщение
В формулировке проблемы теории графов задача о назначении может быть расширена сдвудольных графовпубличные графики. Соответствующая задача поискапаросочетаниявовзвешенном графе, сумма, где весов максимальная, называетсязадачей сопоставления максимального веса.
Еще одно обобщение задачи о назначении — увеличение количества сопоставляемых наборов с двух до многих. Таким образом, вместо предлагаемых агентов с задачами проблема расширяется на регулируемые агенты с задачами, временными интервалами и положениями. Это к представлениюпроблеме многомерного назначения (MAP).
Исследование, описанное в статье про задача о назначениях, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое задача о назначениях и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Из статьи мы узнали кратко, но содержательно про задача о назначениях
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.