Лекция
Привет, сегодня поговорим про типовые задачи исследования операций , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое типовые задачи исследования операций , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
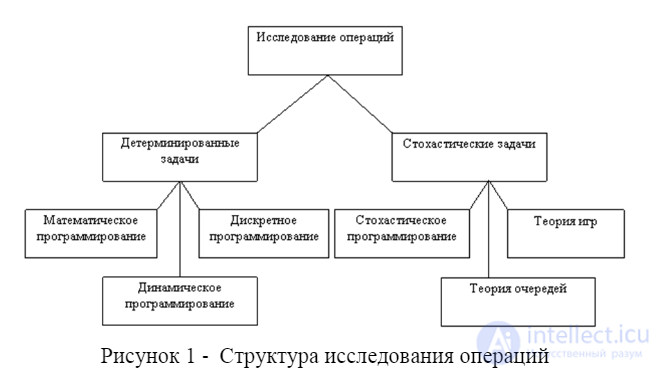
1. Задачи линейного программирования.
Задача о пищевом рационе (Задача хозяйки, задача о солдатской столовой).
Имеются четыре вида продуктов питания: П1, П2, П3, П4. Известная стоимость единицы каждого продукта: С1, С2, С3, С4. Из этих продуктов необходимо составить пищевой рацион, который должен содержать:
- белков не менее b1 единиц,
- углеводов не менее b2 единиц,  (*)
(*)
- жиров не менее b3 единиц.
Единица продукта П1 содержит a11, единиц белков, a12 единиц углеводов, a13 единиц жиров и т.д.
Требуется составить пищевой рацион так, чтобы обеспечить условие (*) при минимальной стоимости продуктов. Построим модель задачи ИО. Обозначим x1, x2, x3, x4 количества продуктов, входящих в рацион. Общая стоимость будет:
L=c1x1+c2x2+c3x3+c4x4 или
L= .
.
Запишем условия для белков, жиров и углеводов
a11x1+a21x2+a31x3+a41x4b1 ;
a12x1+a22x2+a32x3+a42x4b2 ;
a13x1+a23x2+a33x3+a43x4b3 .
Эти условия представляют собой ограничения, накладываемые на решение.
Таким образом, возникает следующая задача ИО: выбрать неотрицательные значения переменных x1, x2,x3, x4 (вектора (x1, x2, x3, x4)), удовлетворяющие системе линейных неравенств (**), при которых линейная функция этих переменных
L= c1x1+c2x2+c3x3+c4x4
обращалась бы в минимум.
С некоторыми модификациями эта задача называется задачей о пайке. Обычно в нее добавляются ограничения:
- вес пайка не должен превышать заданной величины р,
- паек должен быть минимального объема.
Иногда (для пайка) меняются местами целевая функция и ограничение:
- стоимость пайка не должна превышать С денежных единиц;
- паек должен иметь максимальную калорийность.
При этом считается, что для единицы каждого продукта Пk известны объем vk, вес рk и калорийность qk.
Задача о распределении ресурсов.
Имеются какие-то ресурсы (сырье, рабочая сила, оборудование, информация):
R1, R2, …, Rm в соответствующих количествах: b1, b2, …, bm единиц.
С помощью этих ресурсов может производиться конечная продукция (товары):
T1, T2, …, Tn.
Для производства одной единицы товара Tj необходимо aij единиц ресурса Ri (i= , j=
, j=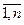 ). Каждая единица ресурса Ri стоит di гривен (i=
). Каждая единица ресурса Ri стоит di гривен (i= ). Каждая единица товара может быть реализована по цене cj ( j=
). Каждая единица товара может быть реализована по цене cj ( j=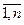 ).
).
По каждому виду товара количество произведенных единиц ограничивается спросом: рынок не может поглотить более, чем kj единиц товара Tj (j=1, 2, …, n).
Какое количество единиц какого товара надо произвести для того, чтобы получить максимальную прибыль?
Обозначим x1, x2, …, xn количества товаров T1, T2, …, Tn , планируемые к производству. Условия спроса налагают следующие ограничения:
x1 k1; x2 k2; …; xn kn.
Ресурсов должно хватить, отсюда ограничения:
an1x1+a12x2+…+a1nxnb1 ;
a21x1+a22x2+…+a2nxnb2 ;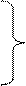
. Об этом говорит сайт https://intellect.icu . . . . . . . . . .
am1x1+am2x2+…+amnxnbm.
Или в более коротком виде:
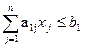 ;
;
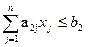 ;
;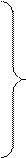
. . . . . .
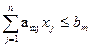
Найдем выражения для прибыли: себестоимость единицы товара Tj равна:
Sj= a1jd1+ a2jd2+ …+ amjdm,
или
Sj= 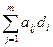 , (j=
, (j=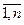 ).
).
Вычислим себестоимость товара каждого вида: S1, S2, …, Sn.
Чистая прибыль qj для товара Tj равна разнице между продажной ценой Cj и себестоимостью Si:
qj =Cj - Sj , (j=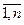 ).
).
Чистые прибыли: q1, q2, …, qn .
Общая прибыль (целевая функция):
L = q1x1 + q2x2 + …+qnxn,
или короче:
L =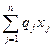 .
.
Выбрать такие неотрицательные значения переменных x1, x2, …, xn, которые удовлетворяют линейным неравенствам и обращают в максимум линейную функцию L.
2.Задачи дискретного программирования.
Особый класс задач составляют задачи дискретного программирования, в котором множество решений является дискретным или в частности целочисленным.
Старинная русская задача.
Сколько надо взять бабушке на базар для продажи живых гусей, уток и кур, чтобы выручить как можно больше денег, если она может взять товара массой не более P кг. Известно, что a1 - масса одной курицы, a2 - масса одной утки, a3 - масса одного гуся, c1,c2 и c3 - их соответствующие стоимости.
Пусть x1, x2, x3 - число кур, уток и гусей, соответственно взятых для продажи. Целевая функция:
c1x1+c2x2+c3x3 =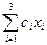
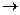 max.
max.
Условие-ограничение - масса товара, который может взять бабушка:
a1x1+a2x2+a3x3P,
x1, x2, x3 Z.
При желании можно учесть конъюнктуру рынка.
Задача о рюкзаке.
Это одна из наиболее популярных задач целочисленного программирования.
Турист готовится к длительному переходу. В рюкзаке он может нести груз массой не более W кг. Этот груз может включать n видов предметов, каждый предмет типа j, массой wj кг, j=. Для каждого вида предмета турист определяет его ценность Ej во время похода. Сколько предметов каждого типа он должен положить в рюкзак, чтобы общая ценность снаряжения была максимальной?
Обозначим через xj – количество предметов j – го типа в рюкзаке. Тогда математическая модель задачи такова:
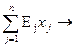 max
max
при ограничениях:
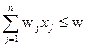 , xj
, xj 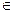 Z (целые).
Z (целые).
xj0, j=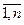 .
.
Это так называемые задачи о неделимостях (Загрузка транспортных средств, план пожарной эвакуации).
3. Задачи динамического программирования.
Задача.
Владелец автомобиля эксплуатирует его в течение m лет. В начале каждого года он может принять одно из трех решений:
1) продать машину и заменить ее новой;
2) отремонтировать и продолжать эксплуатацию;
3) продолжать эксплуатацию без ремонта.
Выбор каждого из трех решений - есть пошаговое управление операцией (один шаг - раз в год). Выбор каждого из трех решений не выражается численно, но можно приписать первому решению число 1, второму - 2, третьему - 3. Как чередовать решения по годам, чтобы суммарные расходы были минимальные?
Показатель аддитивности:
W = 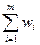 ,
,
где wi – расходы в i-м году. W надо обратить в минимум. Управление может быть таким:
x = (3, 3, 2, 2, 2, 1, 3, …).
А в общем случае это вектор:
x = ( j1, j2, …, jm ),
где j1, j2, …, jm могут принимать значения 1, 2 или 3.
Это особая задача, принадлежащая к классу задач динамического программирования, которые решаются пошагово, а критерий (или выигрыш) складывается из выигрышей на отдельных шагах:
W =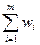
( аддитивный критерий).
Полушутя – полусерьезно Л.Н. Толстой предложил критерий оценки качества человека. Он имел вид дроби, в числителе которой стоят достоинства человека, а в знаменателе – его мнение о себе. Этот критерий логичен только с первого взгляда
( ).
).
4. Задачи на сетях.
Особый класс задач Ио составляют задачи на сетях.
В качестве примера сетевой или потоковой задачи рассматривают транспортную задачу, решенную в 1948г. Ф.Л.Хичкоком.
Транспортная задача.
Пусть есть два завода и три склада. Заводы производят соответственно S1 и S2 единиц продукции, возможности складов – d1,d2,d3 единиц
S1+S2=d1+d2+d3
Задача состоит в том, чтобы минимизировать затраты на перевозку продукции с заводов на склады. Пусть xij – объем продукции, который необходимо перевезти с i-го завода на j-й склад и cij – стоимость перевозки единицы продукции с i-го завода на j-й склад.
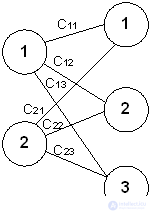
Тогда целевая функция - стоимость перевозки – имеет вид:
c11x11+c12x12+c13x13+c21x21+c22x22+c23x23=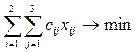
Условие того, что вся продукция будет увезена с каждого завода:
x11+x12+x13=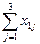 =S1
=S1
x21+x22+x23=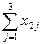 =S2
=S2
Или кратко: 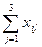 =Si ; i=1,2.
=Si ; i=1,2.
Условие заполнения складов имеет вид:
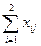 =dj ;
=dj ; 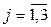
Основы линейного программирования.
Постановка общей задачи линейного программирования (ЛП) и ее анализ.
Если множество допустимых решений 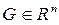 - выпуклый многогранник, а критерий оптимальности – скалярная линейная целевая функция, то задача называется задачей ЛП. Говоря о задачах ЛП, мы фактически имеем в виду не саму задачу ИО, а ее математическую модель, обладающую определенными свойствами.
- выпуклый многогранник, а критерий оптимальности – скалярная линейная целевая функция, то задача называется задачей ЛП. Говоря о задачах ЛП, мы фактически имеем в виду не саму задачу ИО, а ее математическую модель, обладающую определенными свойствами.
Задача ЛП имеет следующий вид:
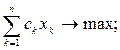
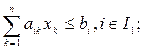
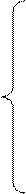
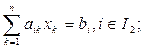
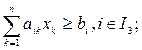
(2.1)
Где aik, ck, bi – известные числовые параметры, а множества I1,I2,I3 попарно не пересекаются и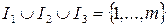 . Неизвестные xk,
. Неизвестные xk, 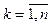 , представляющие собой координаты вектора X (x1,x2,…,xn)Tназывают управляемыми переменными или переменными модели.
, представляющие собой координаты вектора X (x1,x2,…,xn)Tназывают управляемыми переменными или переменными модели.
Рассмотрим пример.
Предприятие производит два вида лака для внутренних и наружных работ. Для производства лаков используются два исходных продукта – А и В. Максимально возможные суточные затраты этих продуктов определяются емкостями, которые имеются, и составляют 6 и 8т соответственно. На производство 1т лака для внутренних работ расходуется 1т продукта А и 2т продукта В, а при производстве 1т лака для внешних работ расходуется 2т продукта А и 1т продукта В.
Изучение рынка показало, что суточный спрос на лак для наружных работ не превышает 2т. Доход от реализации (в тыс. у.е.) 1т лака для внутренних работ равен 3, а доход от реализации 1т лака для внешних работ-2.
Определить какое количество лака каждого вида должна производить компания, чтобы доход от реализации стал максимальным.
Суть этой задачи ИО можно определить следующим образом. Необходимо определить объемы производства каждого вида продукции с учетом ограничений на спрос и с учетом расхода исходных продуктов А и В.
Управляемыми переменными являются x1 – суточный объем выпуска лака для внутренних работ, x2 – суточный объем выпуска лака для наружных работ. Таким образом, n=2.
Суточный расход исходных продуктов А и В не может превосходить максимального суточного запаса, т.е.  и
и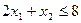 .
.
Ограничение на величину суточного спроса на лак для наружных работ имеет вид . Так как объемы не могут быть отрицательными, то . Таким образом в задаче (2.1) m=3, I1={1,2,3},I2=I3=0.
Общий доход f(x1,x2)=3x1+2x2. Математическая модель рассматриваемой задачи ИО может быть представлена в виде:
3x1+2x2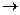 max
max
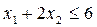 ,
,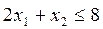 ;
; 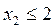 (2.2)
(2.2)
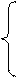
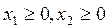
Надеюсь, эта статья об увлекательном мире типовые задачи исследования операций , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое типовые задачи исследования операций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.