Лекция
Привет, сегодня поговорим про транспортные задачи , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое транспортные задачи , задачи хичкока , т-задачи, метод форгеля, метод северо-западного угла, метод минимального элемента, метод наименьшей стоимости , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида. Ее можно рассматривать как задачу об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.
Транспортная задача по теории сложности вычислений входит в класс сложности P. Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределенном количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить ее решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
Пусть имеется пунктов производства некоторого однородного продукта и
пунктов его потребления. Для каждого пункта производства
и для каждого пункта потребления
заданы следующие величины: объем производства {\displaystyle a_{i}}
в пункте производства
, объем потребления
в пункте потребления
, затраты на перевозку единицы продукта
от пункта производства
до пункта потребления
. Предполагается, что суммарное производство равно суммарному потреблению:
. Требуется составить план перевозок, позволяющий полностью вывезти продукты всех производителей, полностью обеспечивающий потребности всех потребителей и дающий минимум суммарных затрат на перевозку. Обозначим как
объемы перевозок от поставщика {\displaystyle i}
до потребителя
.
,
,
Общее представление транспортной задачи (или задачи хичкока , или т-задачи ) показано на рисунке.
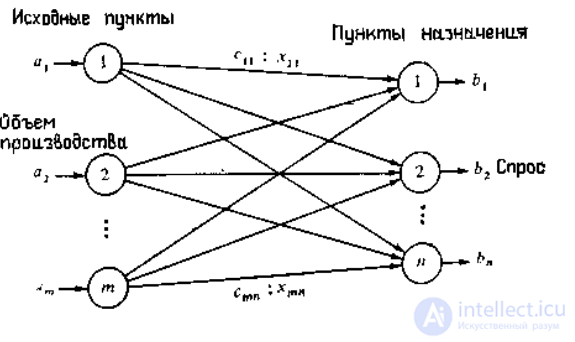
Транспортная задача показана в виде сети с m пунктами отправления и n пунктами назначения, которые показаны в виде узлов сети.
Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i, j), соединяющей пункт отправления i с пунктом назначения j, связаны два вида данных: стоимость cij перевозки единицы груза из пункта i в пункт j и количество перевозимого груза xij. Объем груза в пункте отправления i равен ai, а груза в пункте назначения j - bj. Задача состоит в определении известных величин xij, минимизирующих суммарные транспортные расходы и удовлетворяющие ограничениям на предложение и спрос.
Итак: 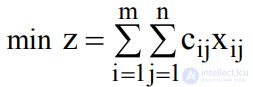 , (1)
, (1)
при ограничениях
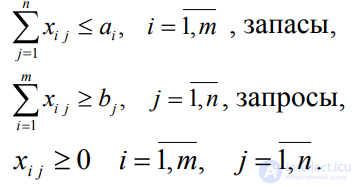
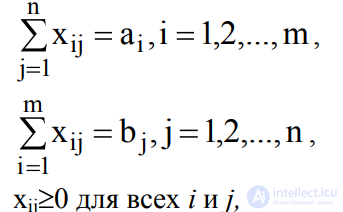 (2) условие полного вывода)
(2) условие полного вывода)
(3) (условие полного удовлетворения спроса)
Таким образом Т-задача есть задача ЛП.
Обычно предполагается, что полный запас груза в пунктах отправления равен суммарному спросу его в пунктах потребления. В этом случае Т-задача называется сбалансированной: 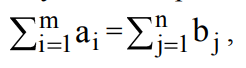 . (4)
. (4)
Т-задача как задача ЛП имеет mn переменных и m+n ограничений в виде равенств. Оказывается, что не все m+n уравнений сформулированной задачи являются линейно независимыми. Действительно, суммируя все уравнения (2) и все уравнения (3), в силу условия (4), мы получаем одно и то же. Следовательно, условия (2) и (3) связаны между собой одной линейной зависимостью и начальный план задачи должен содержать m+n-1 отличных от нуля компонент.
Проблема была впервые формализована французским математиком Гаспаром Монжем в 1781 году . Прогресс в решении проблемы был достигнут во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем . Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.
Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей ее можно решить проще (для задач малой размерности).
Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из в
груза
, а в маленькие клетки — соответствующие тарифы
.
Требуется определить опорный план и путем последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.
На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из или полностью удовлетворяется потребность
.
Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.
Алгоритм:
После нахождения опорного плана перевозок, нужно применить один из алгоритмов его улучшения, приближения к оптимальному.
Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются ребрами бесконечной пропускной способности и цены за единицу потока {\displaystyle C_{ij}}.
К верхней доле искусственно присоединяется исток. Пропускная способность ребер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих ребер равна 0.
Аналогично к нижней доле присоединяется сток. Пропускная способность ребер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих ребер тоже равна 0.
Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Ее решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешевый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана — Форда. При возврате потока стоимость считается отрицательной.
Алгоритм «mincost maxflow» можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма «mincost maxflow» происходит не более чем за {\displaystyle O(v^{2}e^{2})} операций. ({\displaystyle e}
— количество ребер, {\displaystyle v}
— количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка {\displaystyle O(ve)}
операций.
При решении несбалансированной транспортной задачи применяют прием, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.
В этом варианте пункты не делятся на пункты отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление — отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты, включая производитель — производитель, потребитель — потребитель.
Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.
Вариант транспортной задачи в сетевой постановке, при котором задается максимальная пропускная способность некоторых дуг.
Задача решается слегка усложненным методом потенциалов.
Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов). Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам).
Задача решается симплекс-методом (используется разложение Данцига-Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи ).
Пример. Автомобильная компания имеет три завода: в Лос-Анджелесе, Детройте и Нью-Орлеане и два склада в Денвере и Майами. Объемы производства за квартал составляют соответственно: 100, 1500 и 1200 автомобилей. Еженедельная потребность складов составляет 2300 и 1400 автомобилей. Расстояния приведены в таблице:
|
|
Денвер |
Майами |
|
Лос-Анджелес |
1000 |
2690 |
|
Детройт |
1250 |
1350 |
|
Новый Орлеан |
1275 |
850 |
Транспортная компания оценивает свои услуги в 8 центов за перевозку одного автомобиля на одну милю. Стоимость перевозок такова (с округлением до доллара):
|
i |
Денвер (1) |
Майами (2) j |
|
Лос-Анджелес (1) |
80 |
215 |
|
Детройт (2) |
100 |
108 |
|
Новый Орлеан (3) |
102 |
68 |
Задача ЛП формируется так:
z=80x11+215x12+100x21+108x22+102x31+68x32
при ограничениях:
x11+x12=1000 (Л-А)
x21+x22=1500 (Дет)
x31+x32=1200 (Н.О.)
x11+x21+x31=2300 (Ден)
x12+x22+x32=1400 (М)
xij≥0, i=1,2,3; j=1,2.
Задача сбалансирована. Т-задачу записывают в виде так называемой транспортной таблицы.
|
|
Денвер |
Майами |
Объем производства |
|
Лос-Анджелес |
80 x11 |
215 x12 |
1000 |
|
Детройт |
100 x21 |
108 x22 |
1500 |
|
Новый Орлеан |
102 x31 |
68 x32 |
1200 |
|
СПРОС |
2300 |
1400 |
|
Оптимальное решение таково: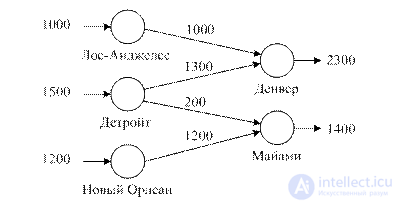
Минимальная стоимость перевозок составляет 3/3 200 долларов.
Когда 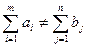 транспортная задача называется несбалансированной. Любую несбалансированную задачу можно сделать сбалансированной. Для этого вводятся фиктивные пункты отправления и назначения.
транспортная задача называется несбалансированной. Любую несбалансированную задачу можно сделать сбалансированной. Для этого вводятся фиктивные пункты отправления и назначения.
Пример. Пусть завод в Детройте уменьшил выпуск до 1300 автомобилей (вместо 1500). Общее количество (3500) меньше общего количества заказанных (3700). Часть заказов складов будет не выполнена.
Так как спрос превышает предложение, для восстановления баланса вводим фиктивный завод (пункт отправления) производящий 3700-3500=200 машин. Поскольку фиктивного завода не существует, назначим нулевую стоимость перевозок от него до складов. В принципе эта стоимость может быть любым положительным числом. Например, чтобы гарантировать все заказы склада в Майами, можно назначить очень высокую стоимость перевозок (штраф) от фиктивного завода до Майами. Так выглядит сбалансированная модель и ее решение.
|
|
Денвер |
Майами |
Объем производства |
|
Лос-Анджелес |
80 1000 |
215
|
1000 |
|
Детройт |
100 1300 |
108
|
1300 |
|
Новый Орлеан |
102
|
68 1200 |
1200 |
|
Фиктивный завод |
0 |
0 200 |
200 |
|
СПРОС |
2300 |
1400 |
|
Решение показывает, что фиктивный завод поставит в Майами 200 автомобилей (т.е. из заказа в 1400 200 автомобилей будет не доставлено)
Предположим, что склад в Денвере заказал всего 1900 автомобилей (предложение превышает спрос). Надо ввести фиктивный пункт назначения, поглощающий разницу. Стоимость перевозок может быть нулевой, или штрафной (большой), если надо вывезти всю продукцию с этого завода.
|
|
Денвер |
Майами |
Фиктивный склад |
Объем производства |
|
Лос-Анджелес |
80 1000 |
215
|
0 |
1000 |
|
Детройт |
100 900 |
108 200 |
0 400 |
1500 |
|
Новый Орлеан |
102
|
68 1200 |
0 |
1200 |
|
СПРОС |
2300 |
1400 |
400 |
|
400 автомобилей из Детройта не востребованы.
Решение транспортной задачи.
В принципе, как задачу ЛП Т-задачу можно решать симплекс-методом. Но ее решают специальным методом, повторяющим шаги симплекс-метода, но с использованием транспортных таблиц.
Пример. Транспортная компания перевозит зерно от 3-х элеваторов к 4-м мельницам. Условия задачи представлены в таблице. Стоимость перевозок приведена в сотнях долларов.
|
|
Мельницы |
|
|||
|
|
1 |
2 |
3 |
4 |
Предложение |
|
1 |
10 x11 |
2 x12 |
20 x13 |
11 x14 |
15 |
|
Элеваторы 2 |
12 x21 |
7 x22 |
9 x23 |
20 x24 |
25 |
|
3 |
4 x31 |
14 x32 |
16 x33 |
18 x34 |
10 |
|
Спрос |
5 |
15 |
15 |
15 |
|
Последовательность решений Т-задачи в точности повторяет схему симплекс-алгоритма.
Шаг 1. Определяем начальное базисное решение. Переходим к шагу 2.
Шаг 2. На основании условия оптимальности симплекс-метода среди небазисных переменных определяем вводимую в базис. Если все небазисные переменные удовлетворяют условию оптимальности, вычисления закончены. Если нет, переходим к шагу 3.
Шаг 3. С помощью условия допустимости среди текущих базисных переменных определяем исключаемую. Находим новое базисное решение. Переходим к шагу 2.
Определение начального решения.
Как мы сказали, имеется m+n ограничений в виде равенств. Поскольку транспортная модель сбалансирована, одно из них должно быть избыточным. Независимых ограничений m+n-1, столько же должно быть и базисных переменных в начальном решении.
Специальная структура Т-модели для построения начального решения позволяет применить три следующих метода.
1. Метод северо-западного угла.
2. метод наименьшей стоимости
3. Метод Фогеля
Выполнение начинается с верхней левой ячейки (северо-западного угла) транспортной таблицы, то есть с переменной x11.
Шаг 1. Переменной x11 присваивается максимальное значение, допустимое ограничениями на спрос и предложение.
Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным предложением (с удовлетворенным спросом). Это означает, что в вычеркнутой строке (столбце) мы не будем присваивать значения остальным переменным (кроме той, которая определена на Шаге 1). Если одновременно удовлетворяются и спрос и предложение, вычеркивается только строка или только столбец.
Шаг 3. Если не вычеркнута только одна строка или только один столбец, процесс прекращается. В противном случае переходим к ячейке справа, если вычеркнут столбец, или к ячейке вниз, если вычеркнута строка. Затем возвращаемся к первому этапу. Последний пример:
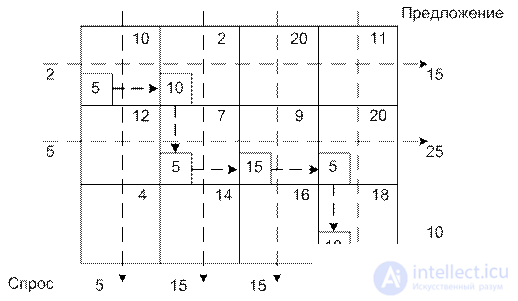
Получено начальное базисное решение.
x11=5; x12=10; x22=5; x23=15; x23=5; x34=10.
Соответствующая стоимость перевозок: 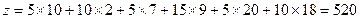 долл.
долл.
Пример 2
. Найти самый дешевый способ удовлетворить спрос в 4-х пунк-тах назначения (магазинах), осуществляя поставки из 3-х исходных (от-правных) пунктов (рис. 1). Затраты на транспортировку даны в таблице 1.
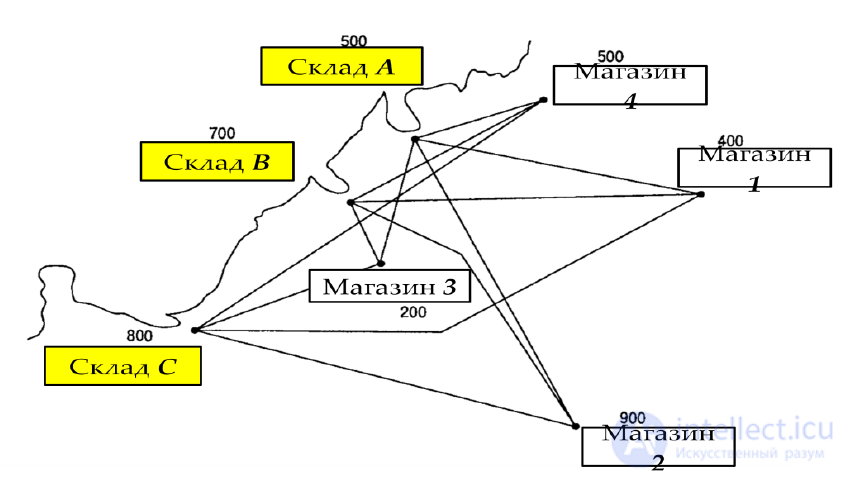
Рис. 1 – Дислокация пунктов отправления и пунктов назначения
Таблица 1 – Удельные затраты на транспортировку

Решение. Построим математическую модель задачи. Данная модель явля-ется сбалансированной, так как суммарный спрос равен суммарному предложению. Целевая функция – минимизация суммарных затрат на транс-портировку со складов в магазины, то есть
120XА1+130XА2 +… + 42XC4→min,
где Xij – количество товара, отправленного со склада i в мага-зин j. В данной модели на переменные решения накладываются следующие ограничения:
а) количество товара, отправленных с любого склада, не может превышать количество товара, имеющегося на складе, то есть, например,
для склада А: XА1+XА2 +XА3+XА4  500
500
б) необходимо удовлетворить спрос во всех магазинах, то есть, например,
для магазина 1: XА1+XB1 +XC1 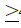 400.
400.
Создадим табличную модель (рис. 2).
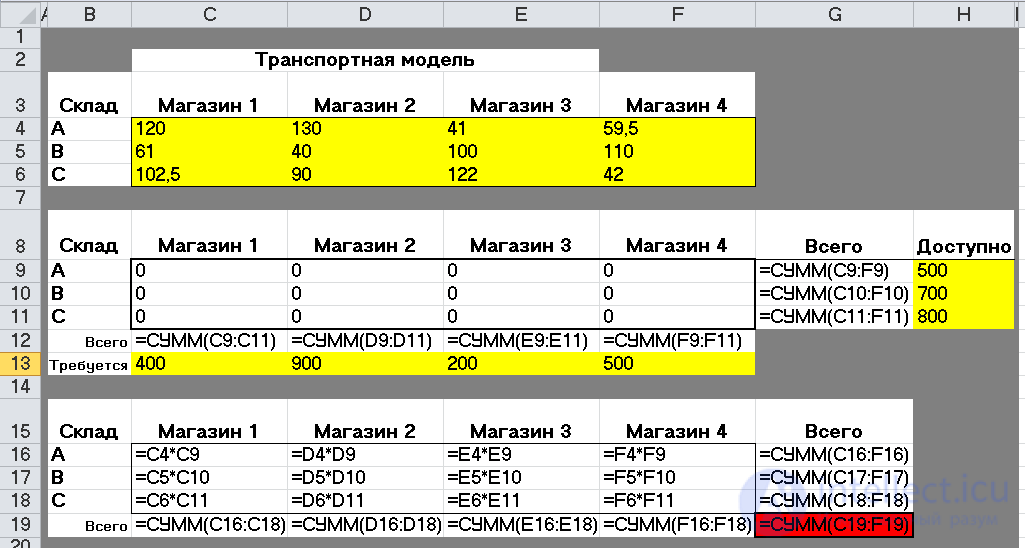
Рис. 2 – Табличная модель
Оптимизируем табличную модель с помощью надстройки Поиск ре-шения (рис. 3).
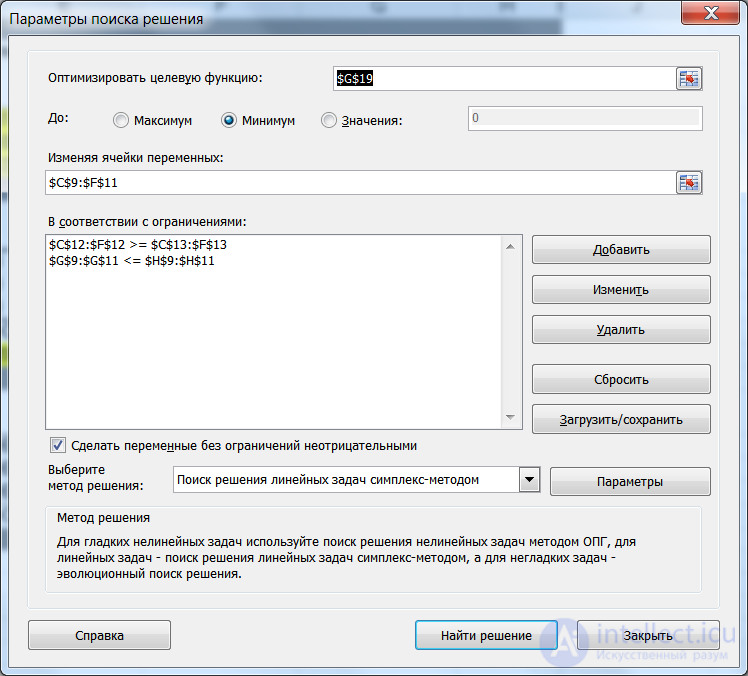
Рис. 3 – Параметры Поиска решения
В результате оптимизации получаем план перевозок с минимальны-ми затратами равными $121 450 (рис. 4).
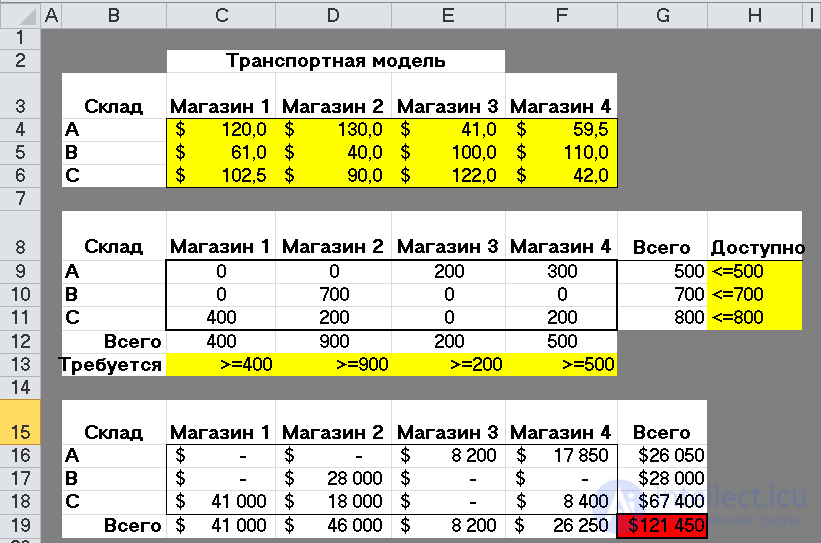
Рис. 4 – Решение
Проанализируем устойчивость модели (рис. 5).
Для этого создадим отчет по устойчивости, который показывает возможности для улучшения значения целевой функции.
Особое внимание следует уделить ограничени-ям, имеющим ненулевое значение теневой цены. Теневая цена показывает, насколько улучшится оптимальное значение целевой функции, если пра-вую часть ограничения увеличить на 1 (для ограничений  ) или уменьшить на 1 (для ограничений
) или уменьшить на 1 (для ограничений 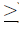 ).
).
Из анализа ограничения на поставку товаров в магазин 2 следует, что уменьшение правой части ограничения на 1 приведет к снижению затрат на $107,5.
Таким образом, если в данный магазин будет требоваться не $900 единиц товара, а $899, то затраты на транспортировку уменьшатся на $107,5.
Увеличение правой части ограничения, отражающего наличие товара на складе B, на 1 приведет к снижению затрат на $67,5. Допустимое увели-чение запаса на данном складе – не более чем на 200 единиц.
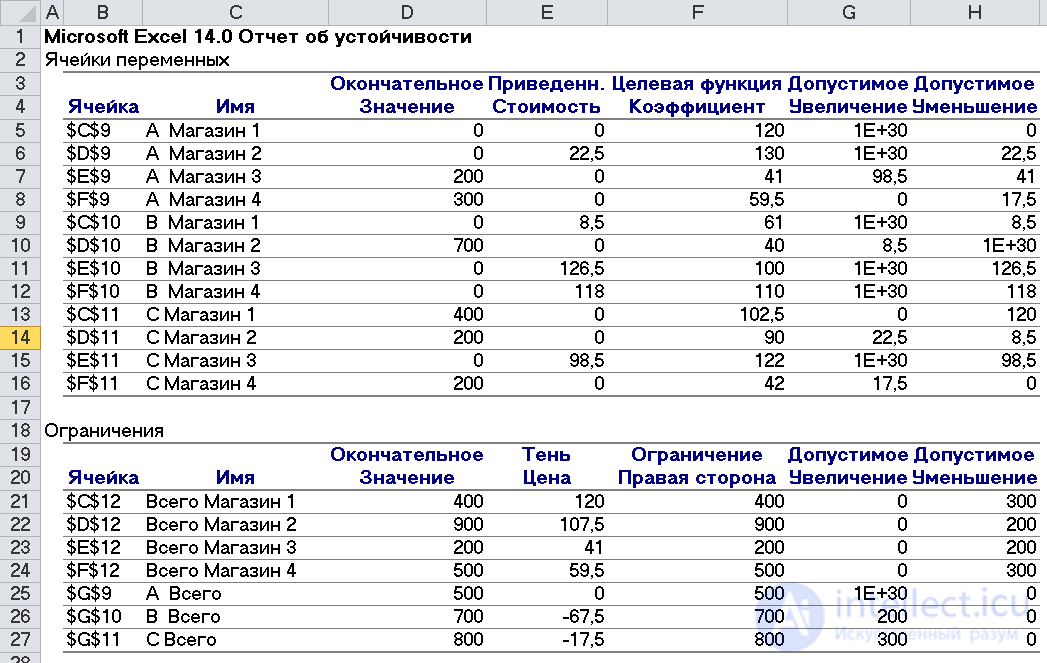
Рис. 5 – Отчет по устойчивости
Этот метод находит лучшее решение, поскольку выбирает переменные, которым соответствуют минимальные стоимости. По всей таблице идет поиск ячейки с минимальной стоимостью. Переменной в этой ячейке присваивается максимально допустимое по спросу и предложению значение. (Если таких переменных несколько, выбор произволен). Вычеркивается соответствующий столбец (строка) и соответственно корректируются спрос-предложение.
Если одновременно выполняются ограничения по спросу и по предложению, вычеркивается или столбец или строка. Просматриваются не вычеркнутые ячейки, выбирается новая ячейка с минимальной стоимостью. Процесс продолжается до тех пор, пока не останутся лишь одна не вычеркнутая строка или столбец.
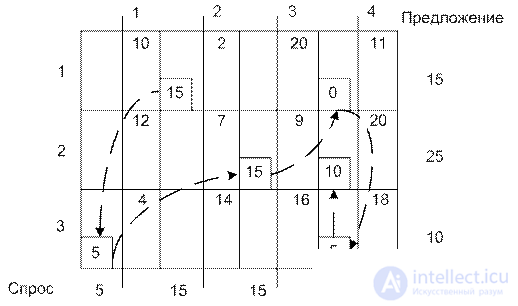
1. Ячейка (1,2)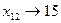 (2 долл) . Вычеркиваем второй столбец. Спрос-предложение первой строки второго столбца равны нулю.
(2 долл) . Вычеркиваем второй столбец. Спрос-предложение первой строки второго столбца равны нулю.
2. Далее ячейка (3,1). 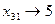 Первый столбец вычеркнем. Ограничение третьей строки по предложению стало 5
Первый столбец вычеркнем. Ограничение третьей строки по предложению стало 5
3. Ячейка (2,3) 15
15
4. Далее  , x34=5, x24=10.
, x34=5, x24=10.
x12=15; x14=0; x23=15; x24=10; x31=5; x34=5.
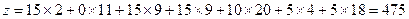 долл.
долл.
Это уже лучше, чем с методом СЗ угла.
Это вариация метода минимальной стоимости, и в общем случае дает лучшее решение.
Шаг 1. Для каждой строки (столбца), которой соответствует строго положительно предложение (спрос), вычисляется штраф путем вычитания наименьшей стоимости из следующей по величине за ней в данной строке (столбце).
Шаг 2. Выделяется строка или столбец с наибольшим штрафом. Если их несколько, выбор произволен. Из выделенной строки или столбца выбирается переменная, которой соответствует минимальная стоимость, и ей присваивается наибольшее значение, допускаемое ограничениями. Корректируются спрос-предложение. Строка или столбец, соответствующие выполненному ограничению, вычеркиваются из таблицы. Если одновременно выполняются ограничения и по спросу и по предложению, вычеркивается только одна строка или один столбец, причем оставшейся строке (столбцу) присваивается нулевое предложение (спрос).
Шаг 3.
а) Если не вычеркнута только одна строка или один столбец с нулевым спросом и предложением, вычисления заканчиваются
б) Если не вычеркнута только одна строка (столбец) с положительным предложением (спросом), в этой строке (столбце) методом наименьшей стоимости находятся базисные переменные и вычисления заканчиваются.
в) Если всем невычеркнутым строкам и столбцам соответствуют нулевые объемы предложения и спроса, методом наименьшей стоимости находятся нулевые базисные переменные и вычисления заканчиваются.
г) Во всех остальных случаях перейти к шагу 1.
|
|
1 |
2 |
3 |
4 |
|
Штрафы для строк |
|
|
10 |
2 |
20 |
11 |
15 |
10-2=8 |
|
|
12 |
7 |
9 |
20 |
25 |
9-7=2 |
|
|
4 |
14 |
16 |
18 |
10 |
14-4=10 |
|
|
5 |
15 |
15 |
15 |
|
|
|
Штрафы для столбцов |
10-4=6 |
7-2=5 |
16-9=7 |
18-11=7 |
|
|
Третья строка имеет наибольший штраф (10). x31 (мин. стоимость)5 Первый столбец вычеркиваем. Пересчитанные штрафы.
|
|
1 |
2 |
3 |
4 |
|
Штрафы для строк |
|
1 |
10 |
2 |
20 |
11 |
15 |
9 |
|
2 |
12 |
7 |
9 |
20 |
25 |
2 |
|
3 |
4 |
14 |
16 |
18 |
5 |
2 |
|
|
0 |
15 |
15 |
15 |
|
|
|
Штрафы для столбцов |
- |
5 |
7 |
7 |
|
|
Теперь наибольший штраф имеет первая строка (9).
x12 (мин стоимость 2)15. Ограничения выполняются и для первой строки и для второго столбца. Вычеркиваем второй столбец. Ресурс первой строки равен нулю. На следующем шаге наибольший штраф будет иметь вторая строка (20-9=11). x23(9) 10. Не вычеркнут только четвертый столбец с положительным неудовлетворенным спросом в 15 ед. Применяем метод наименьшей стоимости к нему и имеем x14=0, x34=5 и x24=10.
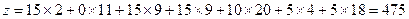 долл
долл
Такое же значение, как и в предыдущем методе. Но приближение обычно лучше.
Надеюсь, эта статья об увлекательном мире транспортные задачи , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое транспортные задачи , задачи хичкока , т-задачи, метод форгеля, метод северо-западного угла, метод минимального элемента, метод наименьшей стоимости и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.