10 Сетевые модели. Алгоритм построения минимального остовного дерева. Алгоритм определения кратчайшего пути. Алгоритм Флойда.

Привет, сегодня поговорим про сетевые модели алгоритм построения минимального остовного дерева алгоритм определения кратчайшего пути алгоритм флойда , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сетевые модели алгоритм построения минимального остовного дерева алгоритм определения кратчайшего пути алгоритм флойда , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

В практической жизни существует масса задач математического программирования, которые можно сформулировать и решить, как сетевые модели (считают, что до 70%). В качестве примеров можно привести:

- проектирование коммуникационных сетей, в том числе компьютерных,

- проектирование сети дорог и поиски кратчайших маршрутов,

- проектирование нефте- , газо- , водопроводов, теплотрасс.

Основные определения.

Сеть состоит из множества узлов, связанных дугами (чтобы согласовать терминологию с теорией графов будем называть дугами только ориентированные ребра, ребро будем употреблять как более общее понятие (и ребро, и дуга), узел сети эквивалентен вершине графа). Сеть описывается парой множеств (N, A), где N- множество узлов, A- множество дуг.

N= { 1, 2, 3, 4, 5},

A={ (1, 2), (1, 3), (2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 5)}.

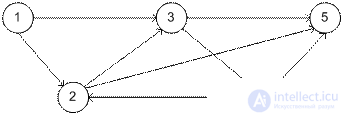
С каждым типом сети связан определенный тип потока. В общем случае потоки в сетях задаются пропускной способностью.

Путем называется последовательность ребер, соединяющих два узла, независимо от направления потока в каждом ребре. Если начальный и конечный узлы совпадают, то путь называется циклом. Например, дуги (2, 3), (3, 4), (4, 2) образуют цикл. Цикл может быть ориентированным, если все дуги ориентированы в одном направлении.

Связная сеть – сеть, у которой любые два узла связаны, по крайней мере, одним путем. Сеть на рисунке именно связная. Деревом называется связная сеть, содержащая подмножество узлов исходной сети и не имеющая циклов. Остовное дерево – это дерево, содержащее все узлы сети.

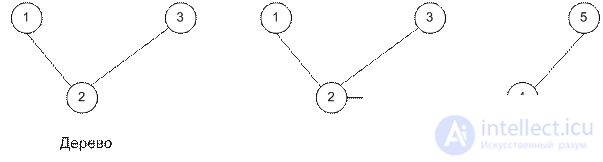
Алгоритм построения минимального остовного дерева.

Алгоритм построения минимального остовного дерева предполагает соединение всех узлов с помощью путей наименьшей длины.

Опишем этот алгоритм. Обозначим через N={ 1, 2, …, n} множество узлов сети и введем обозначения:

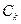– множество узлов сети, соединенных алгоритмом после выполнения k- той итерации этого алгоритма.

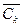 - множество узлов сети, не соединенных с узлами множества после выполнения k-й итерации алгоритма.

k=0. Этап 0.        Полагаем C₀=Ø и 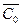=N.

k=1. Этап 1.       

 Выбираем любой узел i из множества 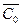  и определяем C₁={i }. Тогда 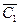= N – {i }. Полагаем k=2.

Основной этап k.

 В множестве 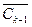  выбираем узел j*, который соединен самой короткой дугой с каким-либо узлом из множества C_k-1. Узел j* присоединяется к множеству C_k-1 и удаляется из множества 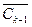. Таким образом, C_k= C_k-1+{ j*}, 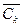=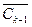- {j*}.

Если множество 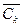 пусто, то выполнение алгоритма заканчивается. В противном случае полагаем k=k+1 и повторяем последний этап.

Пример.

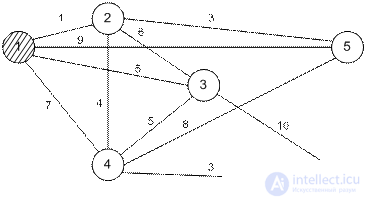
Телевизионная компания планирует подключение к своей кабельной сети пяти новых районов. На рисунке показана структура планируемой сети и расстояния между районами и телецентром. Необходимо спланировать наиболее экономичную кабельную сеть.

Чтобы начать выполнение алгоритма выберем узел 1 (или любой другой). Тогда

C₁={1}, ={2, 3, 4, 5, 6}.

Рассмотрим последовательные итерации. Тонкими линиями показаны ребра, соединяющие узлы, принадлежащие множествам C_k и , среди которых ищется ребро минимальной длины. Найденное ребро показано штриховой линией. Толстыми сплошными линиями показаны ребра, соединяющие узлы множества C_k(которые ранее обозначались штриховыми линиями).

Итерация 1.

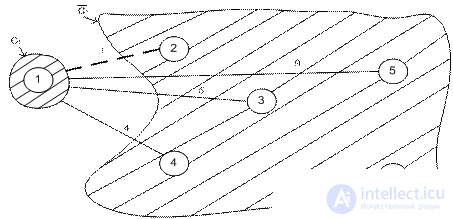
Ребро (1, 2) имеет наименьшую стоимость. Поэтому

j*=2, C₂={1, 2}, 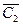={3, 4, 5, 6}.

Итерация 2.

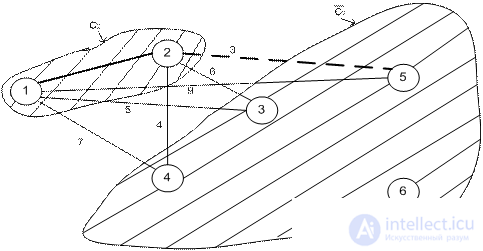
Итерация 3.

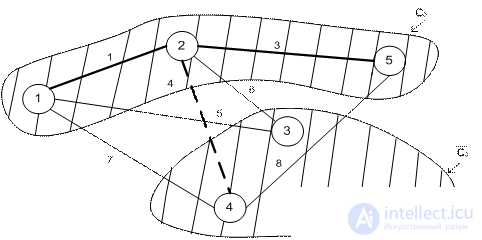
Итерация 4.

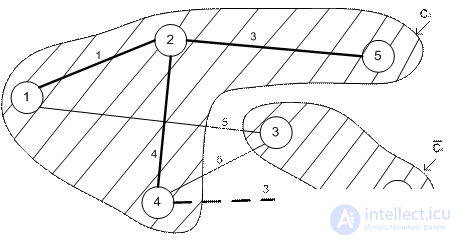
Итерация 5.

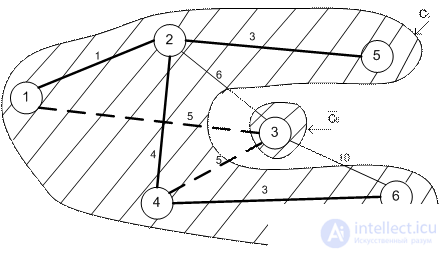
Итерация 6.

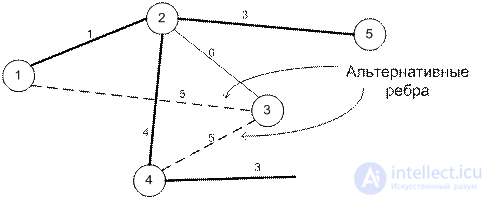
Решение получено на 6-й итерации. Минимальная длина кабеля для построения кабельной сети равна 1+3+4+3+5=16 км.

Алгоритм определения кратчайшего пути.

1.     Алгоритм Дейкстры.

Этот алгоритм разработан для поиска кратчайшего пути между заданным исходным узлом и любым другим узлом сети.

В процессе выполнения этого алгоритма при переходе от узла i к следующему узлу j используется специальная процедура пометки ребер. Обозначим через u_iкратчайшее расстояние от исходного узла 1 до  узла i, через d_ij – длину ребра (i, j). Тогда для узла j определим метку [u_ij, i] следующим образом.

[u_j, i]= [u_i+d_ij, i], d_ij≥0.

Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Об этом говорит сайт https://intellect.icu . Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки меняется на постоянный.

Вычислительная схема алгоритма.

Этап 0.  Исходному узлу (узел 1) присваивается постоянная метка [0, - ]. Полагаем i=1.

Этап 1.   

а)      Вычисляют временные метки [u_i+d_ij, i] для всех узлов j, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку [u_j, k], полученную от другого узла k, и если u_i+d_ij<u_j, тогда метка заменяется на [u_i+d_ij, i].

б)      Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [u_r, s] с наименьшим значением расстояния u_r среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i=r и повторяем этап i.

Пример.    Показана транспортная сеть, соединяющая пять городов с указанными расстояниями. Необходимо найти кратчайшее расстояние от города 1 (узел 1) до всех остальных городов.

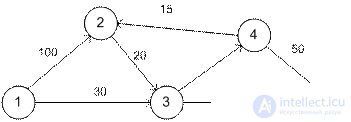
Этап 0.  Назначаем узлу 1 постоянную метку [0, - ].

Этап 1.  Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов.

Среди узлов 2 и 3 узел 3 имеет наименьшее значение расстояния (u₃=30). Поэтому статус метки изменяется на постоянный.

Этап 2.       Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем список меток.

Временный статус метки [40, 3] узла 4 заменяется постоянным (u₄=40).

Этап 3.       Из узла 4 можно достичь узлов 2 и 5.

Временная метка [100, 1], полученная узлом 2 на 2 этапе, заменена на [55, 4]: то есть найден более короткий путь к этому узлу (через узел 4). На третьем этапе узел 5 получает две метки с одинаковым значением расстояния u₅=90.

Этап 4.       Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому список меток такой же, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается.

Алгоритм позволяет производить вычисления только на схеме сети.

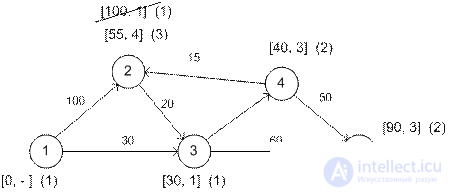
(…)= шаг

Кратчайший маршрут между узлом 1 и любым другим узлом определяется, начиная с узла назначения  путем прохождения их в обратном направлении по меткам. Например, для определения кратчайшего маршрута между узлами 1 и 2 получаем такую обратную последовательность узлов:

(2) → [55, 4] → (4) [40, 3] →(3) → [30, 1] → (1).

Таким образом, получаем путь 1 → 3→ 4→ 2 общей длиной 55км.

Пример.                             Самый надежный маршрут.

Мистер Умник ежедневно ездит на работу на автомобиле. Он определил кратчайший путь от дома до работы. К сожалению, путь усиленно патрулируется ГАИ,и мистера Умника часто останавливают за превышение скорости. Таким образом, самый короткий путь оказывается не самым быстрым. Поэтому мистер Умник планирует разработать новый маршрут, на котором была бы самая высокая вероятность не быть остановленным полицией.

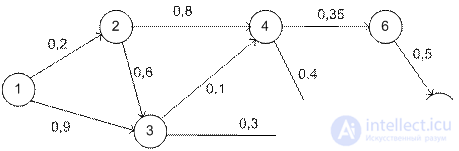
На схеме приведены вероятности не быть остановленным ГАИ для каждого сегмента. Например, вероятность не быть остановленным на маршруте 1→3→5→7 равна 0,9*0,3*0,25=0,0675.

Надо максимизировать вероятность не быть остановленным. Вместо вероятностей можно использовать логарифмы вероятностей:

log p_1k=log p₁+log p₂+…+log p_k.

Поскольку log p_1k≤0 задача эквивалентна минимизации – log p_1k.

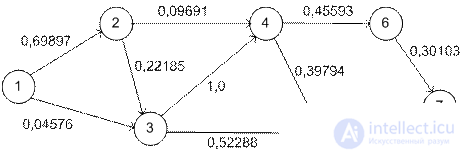
С помощью программы TORA находим кратчайший путь 1→3→5→7 с соответствующей длиной пути 1,1707 (= - log p₁₇), т.о. максимальная вероятность не быть остановленным p₁₇=0,0675.

Алгоритм Флойда.

Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, т.к. он находит кратчайшие пути между любыми двумя узлами сети.

В этом алгоритме сеть представлена квадратной матрицей n×n. Элемент (i, j) равен расстоянию d_ij от узла i к узлу j, которое конечно, если существует дуга (i, j), и равно бесконечности в противном случае.

Основная идея алгоритма Флойда такова. Пусть есть три узла i, j, и k и заданы расстояния между ними.

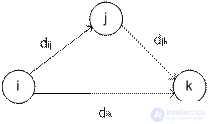
Если выполняется неравенство d_ij+d_jk<d_ik, то целесообразно заменить путь i→k путем i→j→k. Такая замена (будем ее далее называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

Этапы алгоритма.

Этап 0.       Определяем начальную матрицу расстояний D_ij и матрицу последовательности узлов S₀. Диагональные элементы обеих матриц помечаются знаком « - », показывающим, что эти элементы в вычислениях не участвуют. Полагаем k=1.

Основной этап k.                   Задает строку k и столбец k как ведущую строку и ведущий столбец. Рассмотрим возможность применения треугольного оператора ко всем элементам d_ij матрицы D_k-1. Если выполняется неравенство

d_ik+d_kj<d_ij (i≠k, j≠k, i≠j),

то делаем следующее:

а)      создаем матрицу D_k путем замены в матрице D_k-1 элемента d_ij суммой d_ik+d_kj;

b)      создаем матрицу S_k, меняя в матрице S_k-1 элемент S_ij на k. Полагаем k=k+1 и повторяем этап k.

Представим матрицу D_k-1 так:

Строка k и столбец k – ведущие. Строка i – любая с номером от 1 до k-1, строка p – любая с номером от k+1 до n. Аналогично со столбцами. Треугольный оператор выполняется так. Если сумма элементов ведущей строки и столбца (в квадратиках) меньше элементов, находящихся на пересечении строки и столбца (кружки), то расстояние (элемент в кружке) заменяется суммой расстояний, представленных ведущими элементами.

После реализации n этапов алгоритма кратчайший путь i-j определяется так.

1.                Расстояние между узлами i и j равно элементу d_ij в матрице D.

2.                Промежуточные узлы определяются по матрице S_n. Пусть S_ij=k, тогда имеем путь i→k →j. Если далее S_ik=k и S_kj= j, считаем, что весь путь определен, т.к. найдены все промежуточные узлы.

Надеюсь, эта статья об увлекательном мире сетевые модели алгоритм построения минимального остовного дерева алгоритм определения кратчайшего пути алгоритм флойда , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое сетевые модели алгоритм построения минимального остовного дерева алгоритм определения кратчайшего пути алгоритм флойда и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.