Сложность оценки ожидаемых минимаксных значений кратко

Привет, мой друг, тебе интересно узнать все про сложность оценки ожидаемых минимаксных значений, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое сложность оценки ожидаемых минимаксных значений , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

Если бы в программе были заранее известны все выпадения жребия, которые должны произойти в течение остальной части игры, то поиск решения в игре с жеребьевкой был бы полностью аналогичным поиску решения в игре без жеребьевки, который осуществляется минимаксным алгоритмом поиска за время 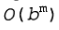. Но поскольку в алгоритме, использующем ожидаемые минимаксные значения, рассматриваются также все возможные последовательности выпадения жребия, для его работы требуется время , где n — количество различных вариантов выпадения жребия.

Даже если глубина поиска ограничена некоторой небольшой величиной d, из-за таких дополнительных затрат времени, намного более значительных по сравнению с минимаксным алгоритмом, в большинстве игр с элементами случайности становится неосуществимым стремление заглянуть в дерево поиска на очень большую глубину. В нардах n равно 21, а b обычно составляет приблизительно 20, но в некоторых ситуациях может достигать величины 4000 для выпадений жребия, включающих повторяющиеся очки. По-видимому, все, на что можно рассчитывать, — это заглянуть вперед на три полухода.

Еще один способ размышления об этой проблеме состоит в следующем: преимуществом альфа-бета-поиска является то, что в нем игнорируются будущие направления развития игры, которые просто не должны быть реализованы, если в игре всегда выбирается наилучший ход. Об этом говорит сайт https://intellect.icu . Поэтому альфа-бета-поиск сосредоточивается на наиболее вероятных событиях. В играх с жеребьевкой вероятных последовательностей ходов не может быть, поскольку, для того, чтобы были сделаны данные ходы, вначале должен выпасть правильный жребий, который сделал бы их допустимыми.

В этом заключается общая проблема, возникающая в любой такой ситуации, когда в картину мира вмешивается неопределенность: количество вариантов дальнейших действий умножается в чрезвычайной степени, а формирование подробных планов действий становится бессмысленным, поскольку мир, скорее всего, будет играть совсем в другую игру.

Несомненно, читателю уже приходила в голову мысль, что к деревьям игр с узлами жеребьевки, по-видимому, можно было бы применить какой-то метод, подобный альфа-бета-отсечению. Как оказалась, такая возможность действительно существует. Анализ узлов MIN и МАХ остается неизменным, но можно также обеспечить отсечение узлов жеребьевки с использованием некоторой доли изобретательности.

Рассмотрим узел жеребьевки С, приведенный на рисунке 6.9, и определим, что будет происходить со значением этого узла по мере исследования и оценки его дочерних узлов. Можно ли найти верхний предел значения С до того, как будут проверены все его дочерние узлы? (Напомним, что именно это требуется в альфа-бета-поиске для того, чтобы можно было выполнить отсечение узла и его поддерева.)

Дерево игры в нарды, кроме узлов МАХ и MIN, должно включать узлы жеребьевки. Узлы жеребьевки обозначены на рис. 6.9 кружками. Ветви, ведущие от каждого узла жеребьевки, обозначают возможные результаты метания жребия, поэтому каждая из них отмечена надписью с указанием количества очков и вероятности, с которой могут быть получены эти очки. Существуют 36 различных сочетаний очков на двух кубиках, и все они являются равновероятными; но поскольку такие сочетания очков, как 6-5 и 5-6, являются одинаковыми, имеется только 21 различимое сочетание очков. Вероятность появления шести дублей (от 1-1 до 6-6) равна 1/36, а каждое из 15 остальных различных сочетаний очков имеет вероятность 1/18.

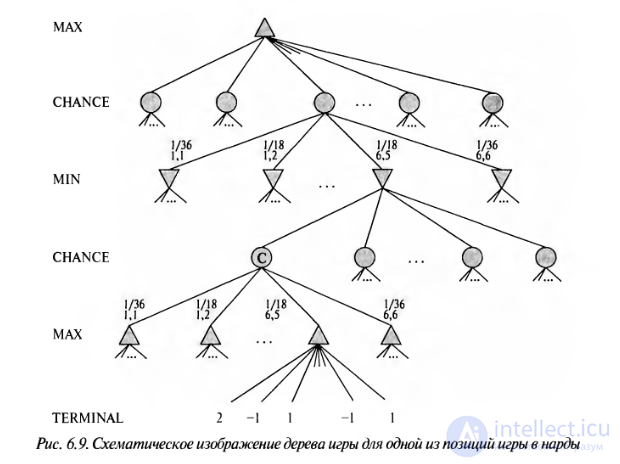
На первый взгляд такое требование может показаться невыполнимым, поскольку значение узла С представляет собой среднее значение его дочерних узлов. А до тех пор пока не будут рассмотрены все выпадения жребия, это среднее может представлять собой что угодно, поскольку сами неисследованные дочерние узлы могут иметь вообще любое значение. Тем не менее, если будут установлены пределы допустимых значений функции полезности, то появится возможность определять пределы и этого среднего.

Например, если будет установлено, что все значения полезности находятся в пределах от +3 до -3, то значения листовых узлов становятся ограниченными, а это, в свою очередь, позволяет установить верхний предел значения узла жеребьевки, не рассматривая все его дочерние узлы.

Если я не полностью рассказал про сложность оценки ожидаемых минимаксных значений? Напиши в комментариях Надеюсь, что теперь ты понял что такое сложность оценки ожидаемых минимаксных значений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.