Лекция
Привет, Вы узнаете о том , что такое плотность упаковки, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плотность упаковки , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..
плотность упаковки в некотором пространстве — это доля пространства, заполненная упакованными телами (фигурами). В задачах упаковки обычно целью является получение упаковки с максимальной возможной плотностью.
Если K1,…,Kn являются измеримыми подмножествами компактного в пространстве с мерой X и их множества внутренних точек попарно не пересекаются, то коллекция {Ki} является упаковкой в X и плотность этой упаковки равна
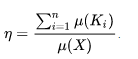 .
.
Если пространство, в которое осуществляется упаковка, бесконечно, как, например, евклидово пространство, плотность традиционно определяется как предел плотностей, получаемых упаковкой в шарах все большего и большего размера.
Если Bt — шар радиуса t с центром в начале координат, то плотность упаковки {Ki : i∈ℕ} равна
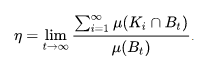 .
.
Поскольку такой предел не всегда существует, полезно определить верхнюю и нижнюю плотности как верхний и нижний пределы. Об этом говорит сайт https://intellect.icu . Если плотность существует, верхняя и нижняя плотности совпадают. Если обеспечено, что любой шар в евклидовом пространстве пересекает лишь конечное число элементов упаковки и если диаметры элементов ограничены сверху, верхняя и нижняя плотности не зависят от выбора начала координат и μ(Ki∩Bt) можно заменить на μ(Ki) для любого элемента, пересекающегося с Bt . Шары можно заменить на гомотетии некоторого другого выпуклого тела, но, в общем случае, полученные плотности могут отличаться.
Часто рассматривается упаковка с ограничением использования элементов некоторого набора элементов. Например, набор элементов может состоять из шаров определенного радиуса. Оптимальная плотность упаковки или константа упаковки, связанная с коллекцией, — это точная верхняя граница верхних плотностей, полученная упаковкой, содержащей подколлекцию набора элементов, из которых создается упаковка. Если заданная коллекция элементов для упаковки состоит из выпуклых тел ограниченного диаметра, существует упаковка, плотность которой равна константе упаковки, и эта константа упаковки не меняется, если шары в определении плотности заменить на гомотетии некоторого другого выпуклого тела .
Представляют интерес все евклидовы движения фиксированного выпуклого тела K. В этом случае константу упаковки называют константой упаковки тела K. Гипотеза Кеплера касается константы упаковки трехмерных шаров. Гипотеза Улама об упаковках утверждает, что трехмерные шары имеют наименьшую константу упаковки по сравнению с другими выпуклыми телами. Все параллельные переносы фиксированного тела также представляют интерес, и для них вводится константа упаковки параллельного переноса тела.
Исследование, описанное в статье про плотность упаковки, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое плотность упаковки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.
Из статьи мы узнали кратко, но содержательно про плотность упаковки
Комментарии
Оставить комментарий
Математические методы исследования операций .Теория игр и расписаний.
Термины: Математические методы исследования операций .Теория игр и расписаний.