Принятие решений

Привет, мой друг, тебе интересно узнать все про принятие решений, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое принятие решений , настоятельно рекомендую прочитать все из категории Математические методы исследования операций .Теория игр и расписаний..

В данном разделе речь идет об играх с двумя игроками, которые будут именоваться МАХ и MIN по причинам, которые вскоре станут очевидными. Игрок МАХ ходит первым, после чего игроки делают ходы по очереди до тех пор, пока игра не закончится. В конце игры игроку-победителю присваиваются очки, а на побежденного налагается штраф. Игра может быть формально определена как своего рода задача поиска с описанными ниже компонентами.

• Начальное состояние, которое включает позицию на доске и определяет игрока, который должен ходить.
• Функция определения преемника, возвращающая список пар (move, state), каждая из которых указывает допустимый ход и результирующее состояние.
• Проверка терминального состояния, которая определяет, что игра закончена. Состояния, в которых игра закончена, называются терминальными состояниями.
• Функция полезности (называемая также целевой функцией, или функцией вознаграждения), которая сообщает числовое значение терминальных состояний. В шахматах результатом является победа, поражение или ничья, со значениями +1, -1 или 0. Некоторые игры имеют более широкий диапазон возможных езультатов; например, количество очков в нардах может составлять от +192 до -192. В настоящем разделе в основном рассматриваются игры с нулевой суммой, хотя будут также кратко упоминаться игры с ненулевой суммой.

Начальное состояние и допустимые ходы каждой стороны определяют дерево игры для данной игры. Из начального состояния игрок МАХ имеет девять возможных ходов. Ходы чередуются так, что мах ставит значок X, a MIN значок О, до тех пор пока не будут достигнуты листовые узлы, соответствующие терминальным состояниям, таким, что один игрок оставил три своих значка в один ряд или заполнены все клетки.

Число под каждым листовым узлом указывает значение полезности соответствующего терминального состояния с точки зрения игрока мах; предполагается, что высокие значения являются благоприятными для игрока МАХ и неблагоприятными для игрока MIN (именно поэтому в теории этим игрокам присвоены такие имена). Задача игрока МАХ состоит в использовании дерева поиска (особенно данных о полезности терминальных состояний) для определения наилучшего хода.

Оптимальные стратегам

При решении обычных задач поиска оптимальное решение для игрока МАХ должно представлять собой последовательность ходов, ведущих к цели — к терминальному состоянию, которое соответствует выигрышу. С другой стороны, в игре участвует также игрок MIN, который имеет другое мнение по этому поводу. Это означает, что игрок МАХ должен найти надежную стратегию, позволяющую определить ход игрока МАХ в начальном состоянии, затем ходы игрока МАХ в состояниях, ставших результатом любого возможного ответа игрока MIN, а затем ходы МАХ в состояниях, ставших результатом любого возможного ответа MIN на те ходы, и т.д. Грубо говоря, оптимальная стратегия приводит к итогу, по меньшей мере, такому же благоприятному, как и любая другая стратегия, в тех условиях, когда приходится играть с противником, не допускающим ошибок. Прежде всего рассмотрим, как найти эту оптимальную стратегию, даже притом что для МАХ часто будет неосуществимой задача ее исчерпывающего вычисления в играх, более сложных, чем крестики-нолики.

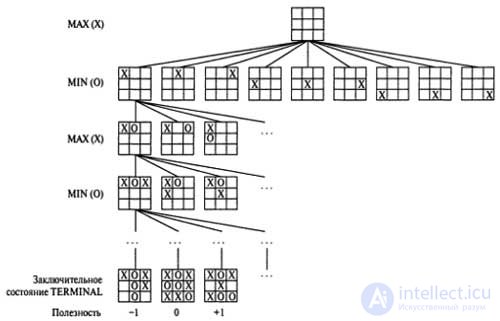(Частичное) дерево поиска для игры крестики-нолики. Верхний узел представляет собой начальное состояние, а первым ходит игрок МАХ, ставя значок X в пустой клетке. На этом рисунке показана часть дерева поиска, в которой демонстрируются чередующиеся ходы игроков MIN (значок О) и МАХ (значок X). Ходы выполняются до тех пор, пока в конечном итоге не будет достигнуто одно из терминальных состояний, которым могут быть назначены данные о полезности в соответствии с правилами игры

Даже такие простые игры, как крестики-нолики, являются слишком сложными, чтобы можно было привести в этой книге для них полное дерево игры, поэтому перейдем к описанию тривиальной игры, показанной на рисунке. Возможные коды игрока МАХ из корневого узла обозначены как аь а2 и а3. Возможными ответами на ход a-i для игрока MIN являются b1, Ь2, Ь3 и т.д. Об этом говорит сайт https://intellect.icu . Данная конкретная игра заканчивается после того, как каждый игрок, МАХ и MIN, сделают по одному ходу. (Согласно терминологии теории игр, это дерево имеет глубину в один ход и состоит из сделанных двумя участниками ходов, каждый из которых называется полуходом.) Полезности терминальных состояний в этой игре находятся в пределах от 2 до 14.

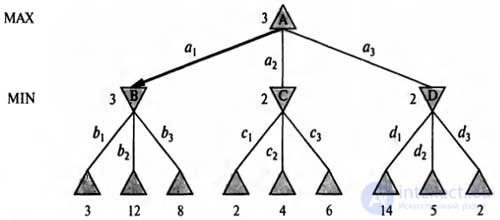Дерево игры с двумя полуходами. Узлы А представляют собой "узлы МАХ", в которых очередь хода принадлежит игроку МАХ, а узлы рассматриваются как "узлы MIN". Терминальные узлы показывают значения полезности для МАХ; остальные узлы обозначены их минимаксными значениями. Лучшим ходом игрока МАХ от корня является а.1, поскольку ведет к преемнику с наибольшим минимаксным значением, а наилучшим ответом MIN является hi, поскольку ведет к преемнику с наименьшим минимаксным значением

При наличии дерева игры оптимальную стратегию можно определить, исследуя минимаксное значение каждого узла, которое можно записать как Minimax-Value (n). Минимаксным значением узла является полезность (для МАХ) пребывания соответствующем состоянии, при условии, что оба игрока делают ходы оптимальным образом от этого узла и до узла, обозначающего конец игры. Очевидно, что минимаксным значением терминального состояния является просто его полезность. Более того, если есть выбор, игрок МАХ должен предпочесть ход, ведущий в состояние с максимальным значением, а игрок MIN — ведущий в состояние с минимальным значением. Поэтому имеет место приведенное ниже соотношение.

Применим эти определения к дереву игры, показанному на рисунке. Терминальные узлы на низшем уровне уже обозначены числами, которые указывают их полезность. Первый узел MIN, обозначенный как B, имеет трех преемников со значениями 3, 12 и 8, поэтому его минимаксное значение равно 3. Аналогичным образом, другие два узла MIN имеют минимаксное значение, равное 2. Корневым узлом является узел МАХ; его преемники имеют минимаксные значения 3, 2 и 2, поэтому сам корневой узел имеет минимаксное значение 3. Можно также определить понятие минимаксного решения, принимаемого в корне дерева: действие a1 является оптимальным выбором для игрока мах, поскольку ведет к преемнику с наивысшим минимаксным значением.

В этом определении оптимальной игры для игрока МАХ предполагается, что игрок MIN также играет оптимальным образом: он максимизирует результат, соответствующий наихудшему исходу игры для МАХ. А что было бы, если игрок MIN не играл оптимальным образом? В таком случае можно легко показать, что игрок МАХ добился бы еще большего. Могут существовать другие стратегии игры против соперников, играющих неоптимальным образом, которые позволяют добиться большего, чем минимаксная стратегия; но эти стратегии обязательно действуют хуже против соперников, играющих оптимально.

Минимаксный алгоритм

Минимаксный алгоритм вычисляет минимаксное решение из текущего состояния. В нем используется простое рекурсивное вычисление минимаксных значений каждого состояния-преемника с непосредственной реализацией определяющих уравнений. Рекурсия проходит все уровни вплоть до листьев дерева, а затем минимаксные значения резервируются по всему дереву по мере обратного свертывания рекурсии.

Например, в дереве, показанном на рисунке, алгоритм вначале выполнил рекурсию с переходом на нижние уровни до трех нижних левых узлов и применил к ним функцию полезности utility, чтобы определить, что значения полезности этих узлов соответственно равны 3, 12 и 8. Затем алгоритм определяет минимальное из этих значений, 3, и возвращает его в качестве зарезервированного значения узла В.

Аналогичный процесс позволяет получить зарезервированные значения 2 для узла С и 2 для узла D. Наконец, берется максимальное из значений 3, 2 и 2 для получения зарезервированного значения 3 корневого узла.

---

Алгоритм вычисления минимаксных решений. Он возвращает действие, соответствующее наилучшему возможному ходу, т.е. действие, ведущее к результату с наилучшей полезностью, в соответствии с предположением, что противник играет с целью минимизации полезности. Функции Max-Value и Min-Value используются для прохождения через все дерево игры вплоть до листьев, что позволяет определить зарезервированное значение некоторого состояния

function Minimax-Decision(state) returns действие action
inputs: state, текущее состояние игры
v <— Max-Value(state)
return действие action в множестве Successors(state) со значением v

function Max-Value(state) returns значение полезности
if Terminal-Test(state) then return Utility(state)
v <— ∞
for a, s in Successors(state) do
v <— Max(v, Min-Value(s))
return v

function Min-Value(state) returns значение полезности
if Terminal-Test(state) then return Utility(state)
v <— ∞
for a, s in Successors(state) do
v <— Min(v, Max-Value(s))
return v

---

Этот минимаксный алгоритм выполняет полное исследование дерева игры в глубину. Если максимальная глубина дерева равна in и в каждом состоянии имеются b допустимых ходов, то временная сложность этого минимаксного алгоритма составляет O(bm). Для алгоритма, который формирует сразу всех преемников, пространственная сложность равна O(bm), а для алгоритма, который формирует преемников по одному, — O(m). Безусловно, в реальных играх такие затраты времени полностью неприемлемы, но данный алгоритм служит в качестве основы математического анализа игр, а также более практичных алгоритмов.

Оптимальные решения в играх с несколькими игроками Многие популярные игры допускают наличие больше чем двух игроков. Рассмотрим, как можно распространить идею минимаксного алгоритма на игры с несколькими игроками. С точки зрения технической реализации это сделать несложно, но при этом возникают некоторые новые и интересные концептуальные проблемы. Вначале необходимо заменить единственное значение для каждого узла вектором значений. Например, в игре с тремя игроками, в которой участвуют игроки А, B и С, с каждым узлом ассоциируется вектор . Для гтерминальных состояний этот вектор задает полезность данного состояния с точки зрения каждого игрока. (В играх с двумя игроками и нулевой суммой двухэлементный вектор может быть сокращен до единственного значения, поскольку значения в нем всегда противоположны.)

Простейшим способом реализации такого подхода является применение функции Utility, которая возвращает вектор значений полезности. Теперь необходимо рассмотреть нетерминальные состояния. Рассмотрим узел в дереве игры, показанном на рисунке, который обозначен как X. В этом состоянии игрок С выбирает, что делать. Два варианта ведут к терминальным состояниям с векторами полезности и . Поскольку 6 больше чем 3, игрок С должен выбрать первый ход. Это означает, что если достигнуто состояние X, то дальнейшая игра приведет к терминальному состоянию с полезностями . Следовательно, зарезервированным значением X является этот вектор. Вообще говоря, зарезервированное значение узла п представляет собой вектор полезности такого узла-преемника, который имеет наивысшее значение для
игрока, выбирающего ход в узле n.

Любой, кто играет в игры с несколькими игроками, такие как Diplomacy™ ("Дипломатия"), быстро узнает, что в них происходит гораздо больше событий, чем в играх с двумя игроками. В играх с несколькими игроками обычно создаются альянсы между игроками, либо формальные, либо неформальные. К тому же иногда по мере развития игры альянсы то формируются, то разрушаются. Как можно понять такое поведение? Являются ли альянсы естественным следствием выбора оптимальных стратегий для каждого игрока в игре с несколькими игроками? Как оказалось, они действительно могут стать таким следствием. Например, предположим, что игроки Айв имеют слабые позиции, а игрок С— более сильную позицию.

В таком случае и для А, и для В часто бывает оптимальным решение атаковать С, а не друг друга, поскольку иначе С уничтожит каждого из них по отдельности. Таким образом, сотрудничество становится следствием чисто эгоистичного поведения. Безусловно, как только игрок С ослабнет под совместным натиском, альянс потеряет свой смысл и соглашение может нарушить либо игрок А, либо игрок В. В некоторых случаях явно выраженные альянсы просто становятся конкретным выражением того, что и так произошло бы. А в других случаях попытка нарушить альянс вызывает общественное осуждение, поэтому игроки должны класть на весы немедленно достигаемую выгоду от нарушения альянса и долговременный убыток, возникающий из-за того, что их не будут считать заслуживающими доверия.













Если игра не имеет нулевую сумму, то сотрудничество может также возникать даже при наличии всего двух игроков. Допустим, что имеется терминальное состояние с полезностями и что 1000 — максимальная возможная полезность для каждого игрока. В таком случае оптимальная стратегия для обоих игроков заключается в том, чтобы делать все возможное для достижения этого состояния; это означает, что игроки автоматически вступают в сотрудничество для достижения обоюдно желаемой цели.

Если я не полностью рассказал про принятие решений? Напиши в комментариях Надеюсь, что теперь ты понял что такое принятие решений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические методы исследования операций .Теория игр и расписаний.