Построение функций полезности в условиях вероятностной неопределенности кратко

Привет, Вы узнаете о том , что такое Построение функций полезности в условиях вероятностной неопределенности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Построение функций полезности в условиях вероятностной неопределенности , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Поскольку каждое вероятностное распределение порождает некоторую случайную величину, то можно говорить, что каждая альтернативах, выбираемая ЛПР, порождает случайную величину %г. Таким образом, можно сравнивать не только сами распределения, но и порождаемые ими случайные величины. Отношение предпочтения на множестве случайных величин можно построить с помощью функций полезности или функций риска. Понятие функции полезности для задачи принятия решений в условиях определенности было введено в параграфе 7.3. В случае задачи принятия решений в условиях неопределенности необходимо модифицировать данное понятие.

Определение

Полезностью (/(%) случайной величины ?, будем называть математическое ожидание величины и(?):

если такое математическое ожидание существует. При этом и — есть некоторая неубывающая функция. Сама функция ?/, ставящая в соответствие каждой случайной величине ее математическое ожидание, называется функцией полезности.

Замечание. Об этом говорит сайт https://intellect.icu . Иногда на функцию и накладывают более жесткие ограничения, например, свойство вогнутости .

Функция полезности порождает отношения предпочтения на множестве функций распределения ? следующим образом

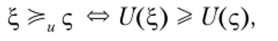
т.е. случайная величина ?, не менее предпочтительна, чем в том и только в том случае, если {/(?) > Щс).

Пример функции полезности. Рассмотрим функцию и(?) = 1 - ехр(-2?), ? > 0. Тогда для случайной величины 2;, имеющей равномерное распределение на отрезке [0, 11, полезностью будет число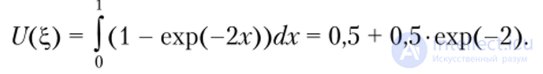

Обратите внимание!

Поскольку функция полезности определена для каждой альтернативы х е Х} она является функцией от т.

Заметим, что отношения стохастического доминирования тоже можно задать с помощью функций полезности. Пусть F{t) и G(t) — функции распределения случайных величин ?,г и 2;~ соответственно, где х> х е X. Можно доказать , что если существуют математические ожидания Щх) и U(x) для всех неубывающих функций и> то:

С <, Т7тогда и только тогда, когда ?/(С) < Щ!7) для всех возрастающих функций и;

С <п Т7 тогда и только тогда, когда < ЩР) для всех неубывающих строго вогнутых функций и.

• Свойство вогнутости часто называют свойством выпуклости вверх. Говорят, что функция и обладает свойством вогнутости, если для всяких х и г/, принадлежащих области определения функции и, и а € (0, 1) верно следующее неравенство и(ах + (1 - а)у) > аи(х) ++ (1-а )и(у).
• Fishbum Р. С. Convex stochastic dominance with continuous distribution functions //J. Econ. Theory. 1974. V. 6. P. 143-158.

Исследование, описанное в статье про Построение функций полезности в условиях вероятностной неопределенности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Построение функций полезности в условиях вероятностной неопределенности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений