Лекция
Привет, Вы узнаете о том , что такое Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства , настоятельно рекомендую прочитать все из категории Теория принятия решений.
Отношение (9.1) остается и при т > 2 отношением строгого частичного порядка , т.е. обладает свойствами антирефлексивности (у > у — не выполнено), антисимметричности ((у > у*) А (у* >у)=* (у = У*)) и транзитивности ((у > у*) А А (у* > у**) => (у > у**)).
Обратите внимание!
В отличие от Л , в пространстве Л"' существуют пары векторных критериев у, у*, как удовлетворяющие отношениям у > у* или у* > у, так и не удовлетворяющие ни одному из этих отношений. Таким образом, критериальное пространство Л™ — частично упорядоченная группа .
Проиллюстрируем смысл критериального пространства как частично упорядоченной группы геометрически для случая т = 2, т.е. для двух критериев /,(х) и/2(х). При т = 3, т.е. в критериальном пространстве Л , геометрическая интерпретация становится менее наглядной. Приведем два примера, отвечающие двум часто встречающимся (и в теории, и на практике) вариантам множества альтернатив X: дискретному случаю и области возможных вариантов.
Пример: дискретное множество альтернатив. Если множество решений X с Л дискретно , т.е. все его точки изолированы , то оно может быть либо конечным (X = {хр х2,хп}), либо счетным множеством (X = {х,, х2,..., хп,...}). На практике ситуация конечного множества может возникнуть, если имеется несколько (например, п = 10) вариантов приобретаемого товара, представленных проектов и т.н. Критериями г/, и у0 в этом случае могут быть, в частности, цена и качество (товара, проекта).
Каждой альтернативе хк с номером к сопоставим точку Ук плоскости 9?2 с координатами г/, = /{(хк) и у2 = /2(хк). Тогда графическое представление при п = 10 множества возможных оценок У = {ух, у2,..., г/10} в критериальном пространстве 9?2 представляет собой набор изолированных точек {Ур У2,..., У10} (рис. 9.1). Отметим, что согласно введенному вначале предположению критерий, отвечающий цене (скажем, ух), подвергнут преобразованию М - /{(х) так, что минимальной цене соответствует максимальное значение г/,. В данной ситуации отношение строгого порядка, введенное формулами (9.1), можно интерпретировать в терминах предпочтений ЛГ1Р следующим образом. Если две оценки ух и ук удовлетворяют отношению у. > ук, то точка У- лежит правее и выше точки Ук, и тогда ЛПР может исключить вариант ук как явно менее предпочтительный по сравнению с у..

Рис. 9.1. Дискретное множество возможных оценок У в двумерном критериальном пространстве 9?2 и образ соответствующего множества Парето — Эджворта
Из рис. 9.1 очевидно, что, хотя множество возможных оценок У и не является линейно упорядоченным множеством, т.е. Об этом говорит сайт https://intellect.icu . все 10 альтернатив нельзя выстроить в определенном порядке, но частичная упорядоченность группы позволяет выделить из множества Уточки У1? У2, У^ и У8, расположенные на рис. 9.1 правее и выше всех остальных вариантов. Иными словами, при выборе наилучшего решения ЛПР может убрать из рассмотрения все остальные альтернативы и выбирать только из четырех: х,, х2, х4 и х8. Между собой эти варианты несравнимы согласно формуле (9.1). Величины критериев у] и у2 достигают максимума в различных точках: критерий г/, достигает максимума в точке У8, тогда как величинау2 — в точке Ух, т.е. одновременный максимум на множестве X не реализуется. Промежуточные варианты У2 и У4 представляют собой компромиссные решения, которые вполне могут соответствовать предпочтениям ЛПР.
Такое сужение множества альтернатив X с исходных 10 до четырех, само собой разумеющееся при взгляде на иллюстрацию, перестает быть наглядным в случае критериальных пространств более высоких размерностей т или же для более сложных множеств альтернатив X. Именно изучение в самом общем случае этого сужения, именуемого множеством Парето — Эджворта, и составляет предмет данной главы.
Следующий пример более сложного множества альтернатив X естественно было бы назвать непрерывным множеством (так как непрерывность - общепринятое противопоставление дискретности ), но формально в математике непрерывными считают исключительно линейно упорядоченные множества . Как мы убедились, линейная упорядоченность уже при т = 2 отсутствует. Поэтому назовем множество X областью, представляющей собой с точки зрения топологии связное подмножество топологического пространства. Нередко областью считают только открытое множество, но для теории принятия удобнее рассматривать замкнутую область, т.е. замыкание области, включающее также границу.
Пример: область как множество альтернатив. Если множество решений X связно, то между любыми «соседними» по величинам критериев альтернативами всегда могут быть промежуточные варианты. Тогда X обязано быть несчетным множеством. Подобная ситуация возникает, в частности, при выборе оптимальных значений двух управляющих параметров (финансовых регуляторов, технических показателей и т.п.) некоторой системы при условии, что регулировка этих параметров может осуществляться непрерывно в некоторых пределах. Графическое представление множества возможных оценок У в критериальном пространстве может иметь вид наподобие фигуры У, заштрихованной на рис. 9.2.
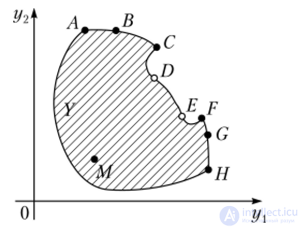
Рис. 9.2. Область возможных оценок У в двумерном критериальном
пространстве и образ соответствующего множества Парето — Эджворта
Как и на рис. 9.1, координаты каждой точки на рис. 9.2 (например, координаты точек А, В, С, I), Е, В, С, Я, М) представляют собой величины критериев ух и у2 для некоторой альтернативы из множества X. Но здесь, если ЛПР стремится достичь наибольшего значения обоих критериев у{ и у2, т.е. требуется их максимизация, то частичная упорядоченность группы позволяет ЛПР выделить из множества X альтернативы с образами из отрезков ВС, ОЕ и ВС границы заштрихованной области У, расположенными, как и на рис. 9.1, правее и выше всех остальных вариантов. Иными словами, при выборе наилучшего решения ЛПР может убрать из рассмотрения все остальные альтернативы с векторными оценками из заштрихованной области У и выбирать только точки трех указанных отрезков.
3
Обратите внимание!
Концы отрезков ВС и ГС остаются в числе представляющих интерес для ЛПР, а концы отрезка ОЕ — нет, так как они доминируемы точками С и Л соответственно.
В данном случае сужение множества альтернатив, само собой разумеющееся при взгляде на рис. 9.2, тем более (по сравнению с рис. 9.1) перестает быть очевидным в случае критериальных пространств более высоких размерностей п или же для более сложных множеств альтернатив X.
Обратите внимание!
Приведенные два примера показывают важность сужения множества возможных оценок У. Если в нервом примере выбор из 4 альтернатив становится значительно проще, чем первоначальный выбор из 10 вариантов, то во втором — не просто уменьшается число альтернатив, но происходит качественное преобразование первоначальной области У с конечной площадью в объединение отрезков кривой линии, имеющих нулевую площадь.
Получаемое в результате сужение множества альтернатив X называется множеством Парето — Эджворта (Френсис Эджворт1 (Francis Edgeworth, (1845—1926) — английский экономист, родившийся в Ирландии, который впервые, раньше В. Парето, ввел понятие Парето-оптимального решения для двух критериев). Именно с построения этого множества начинается анализ любой задачи теории принятия решений. Практическое применение указанного алгоритма показывает, что нередко, как и в двух приведенных примерах, сужение X и построение множества Парето — Эджворта настолько ограничивает множество оставшихся вариантов, что дальнейший выбор достаточно несложен и не составляет труда для ЛПР.
Определение
Множеством Парето — Эджворта, или множеством Парето-оптималъных решений, называется множество Р/(Х) входящих в X альтернатив х*, которые не являются доминируемыми, т.е. для которых не существует доминирующих альтернатив х, удовлетворяющих отношению строгого предпочтения: х > х*.
Из определения вытекает, что для построения множества Парето - Эджворта необходимо исключить из множества решений X все доминируемые альтернативы. Иными словами, надо отбросить все такие альтернативы х*, для которых найдется хотя бы одна доминирующая альтернатива х > х*.
Обратите внимание!
Практическая значимость множества Парето — Эджворта обусловлена тем, что любое решение х из множества альтернатив X, не входящее в РДХ), заведомо не может быть оптимальным.
Действительно, по определению решение х будет доминируемым по отношению к некоторому элементу х* множества Парето — Эджворта, т.е. ЛПР предпочтет х* вместо х.
Парето-оптимальным решениям в критериальном пространстве отвечают Парето-оптимальные векторы (оценки).
Определение
Парето-оптимальным вектором (или Парешо-оптималъной векторной оценкой) называется вектор /2(.г*), /т(х*)), соответствующий Парсто-опти-
мальному решению х*.
Приведенные примеры позволяют сделать вывод, что главный смысл рассмотрения Парето-оптимальных вариантов и их векторных оценок состоит в значительном сужении исходных множеств X и У, причем любая из оставшихся альтернатив в силу недоминируемости может быть признана оптимальной (лучшей).
Обратите внимание!
Парето-оптимальные варианты благодаря свойствам своих векторных оценок образуют существенно более узкое по сравнению с первоначальным множеством X множество Парето — Эджворта Р^Х). Тем самым окончательный выбор ЛПР наилучшего эффективного решения становится намного легче и проще.
Наряду с множеством недоминируемых альтернатив рассматривается и множество недоминируемых векторных оценок.
Определение
Множество Парето-оптимальных векторных оценок, т.е. образ множества Парето — Эджворта РХХ) в критериальном пространстве называют фронтом Парето[10] (иногда Парето-фронтом — от англ. Pareto-frontier) или множеством Парето — Эджворта в критериальном пространстве.
Из свойств алгебраической структуры, обусловленных линейной упорядоченностью группы, вытекает важное свойство Парето-оптимальных векторных оценок.
Обратите внимание!
Парето-оптимальные векторные оценки остаются Парето-оптимальными при любых линейных преобразованиях отдельных частных критериев, сохраняющих порядок.
Иначе говоря, такие преобразования шкал измерения, как параллельный перенос (сдвиг) вдоль любой оси критериального пространства или изменение масштаба (т.е. единиц измерения) с положительным коэффициентом, не меняют свойства Парето-оптимальности.
Исследование, описанное в статье про Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Парето-оптимальные (эффективные) векторные оценки и варианты, их свойства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений
Комментарии
Оставить комментарий
Теория принятия решений
Термины: Теория принятия решений