Построение отношений предпочтения для многокритериальной ЗПР кратко

Привет, Вы узнаете о том , что такое Построение отношений предпочтения для многокритериальной ЗПР, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Построение отношений предпочтения для многокритериальной ЗПР , настоятельно рекомендую прочитать все из категории Теория принятия решений.

Выделив для решаемой ЗПР набор критериев оценки, недостаточно уметь сравнивать альтернативы по каждому отдельному критерию. Необходимо уметь их сравнивать комплексно по всему имеющемуся набору критериев, т.с. нужно сравнивать векторы (/,(*),/;(х), ...,/т(х)) а У для различных значений х е X. Для этого введем бинарные отношения предпочтения на множестве возможных векторных оценок У. Рассмотрим два наиболее часто встречающиеся на практике отношения.

Определение

Говорят, что вектор у = (г/,, у2,..., ут) е УГ" доминирует по Парето вектор у = = (г/,, у2,..., ут) е 9Г, если для всех г = 1,2,..., т выполняется неравенство у{ > у; и хотя бы для одного значения индекса это неравенство является строгим. Обозначается у > г/,.

Отношение доминирования по Парето является отношением строгого предпочтения.

Другое отношение предпочтения строится с помощью последовательного покоординатного сравнения двух векторов между собой.

Определение

Говорят, что вектор у = (у,,у2, —,Ут) е '.Н"‘ доминирует по отношению лексикографического предпочтения вектор у = (ур у2,..., ут) е ЧЯт, если существует такое число к= 1,2,..., т, что выполняются соотношения

Обозначается у у. Об этом говорит сайт https://intellect.icu .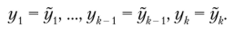

Для построения отношения лексикографического предпочтения используется следующая процедура. Сначала две альтернативы сравниваются между собой по первому критерию, и если оказалось, что их оценки по этому критерию совпадают, то их сравнивают по второму критерию. Если же оценки альтернатив совпадают и по второму критерию, то их сравнивают но третьему и т.д., пока по какому-либо критерию не будет найдено различие. В противном случае оценки будут совпадать по всем критериям, а значит, эти альтернативы будут равнозначны для ЛПР.

Недостатком использования такого отношения предпочтения для решения ЗПР является то, что фактически принимается во внимание только первый или несколько первых критериев, так как сравнение по следующим критериям в списке происходит только в том случае, если по предыдущим не было найдено оптимальное решение. Разные варианты ранжирования критериев могут существенно изменить принимаемые решения.

Если для выявления наиболее предпочтительного производителя в примере (**) применить отношение лексикографического предпочтения, то в описанной постановке задачи «победителем» будет производитель 3. Однако, если критерии расположить в другом порядке, например, первым поставить оценку по привлекательности цены товара, то «наилучшим» будет производитель 1.

Определение

Отношение предпочтения > называется непрерывным на У с: 9?™, если множество {(уу г) | у > 2, у, 2 е У) является открытым подмножеством У .

Данное определение означает, что если у строго предпочтительнее у, то малое изменение каждого из этих элементов сохранит отношение предпочтения у > у.

Заметим, что отношение лексикографического предпочтения не является непрерывным. Поясним это на следующем примере.

Пример нарушения свойства непрерывности отношением лексикографического предпочтения. Пусть имеются два критерия: У <= 9? и для векторных оценок у = (г/,, г/2), г = (г,, г2) верно г/, = гх, у2 > г2. При этом заметим, что будет выполнено у г. Однако, уменьшив ух на любое малое число, получим ух < г{, что даст у < 1 2.

• Определения понятий бинарные отношения и отношения предпочтения вводились в параграфе 7.2.
• В данном случае предполагается, что в пространстве 9?'" введена некоторая метрика.
• Множество является открытым, если каждый его элемент принадлежит множеству вместес некоторой своей е-окрестностью, где ? > 0. При этом ?-окрестностью элемента называетсямножество элементов множества, таких что расстоянии до него не превышает ?.
• Множество является открытым, если каждый его элемент принадлежит множеству вместес некоторой своей е-окрестностью, где ? > 0. При этом ?-окрестностью элемента называетсямножество элементов множества, таких что расстоянии до него не превышает ?.

Исследование, описанное в статье про Построение отношений предпочтения для многокритериальной ЗПР, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Построение отношений предпочтения для многокритериальной ЗПР и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория принятия решений