Лекция
Game: Perform tasks and rest cool.5 people play!
Play gameПривет, Вы узнаете о том , что такое коническое сечение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое коническое сечение, коника , настоятельно рекомендую прочитать все из категории Стереометрия.
коническое сечение , или коника , — пересечение плоскости с поверхностью кругового конуса. Существует три главных типа конических сечений: эллипс, парабола и гипербола, кроме того, существуют вырожденные сечения: точка, прямая и пара прямых. Окружность можно рассматривать как частный случай эллипса. Кроме того, параболу можно рассматривать как предельный случай эллипса, один из фокусов которого бесконечно удален.
Конические сечения могут быть получены как пересечение плоскости с двусторонним конусом
(в декартовой системе координат)
Здесь
— угол между образующей конуса и его осью.
Если плоскость проходит через начало координат, то получается вырожденное сечение. В невырожденном случае,
Уравнение кругового конуса квадратично, стало быть, все конические сечения являются квадриками, также все квадрики плоскости являются коническими сечениями (хотя две параллельные прямые образуют вырожденную квадрику, которая не может быть получена как сечение конуса, но она может быть получена как сечение цилиндра — вырожденного конуса, и обычно считается «вырожденным коническим сечением»).
Game: Perform tasks and rest cool.5 people play!
Play gameВ математике , А коническое сечение (или просто коническая ) представляет собой кривую получается как пересечения поверхности в виде конуса с плоскостью . Три типа конического сечения: гипербола , парабола и эллипс ; круг является частным случаем эллипса, хотя исторически это иногда называют четвертым типом. Древнегреческие математики изучали конические сечения, кульминацией которых стала систематическая работа Аполлония Пергского над их свойствами около 200 г. до н.э.
Конические сечения на евклидовой плоскости обладают различными отличительными свойствами, многие из которых могут использоваться в качестве альтернативных определений. Одно такое свойство определяет некруглую конику как набор тех точек, расстояние от которых до некоторой конкретной точки, называемой фокусом , и некоторой конкретной линии, называемой директрисой , находится в фиксированном соотношении, называемом эксцентриситетом . Тип конуса определяется величиной эксцентриситета. В аналитической геометрии конику можно определить как плоскую алгебраическую кривую степени 2; то есть как набор точек, координаты которых удовлетворяют квадратному уравнениюв двух переменных. Это уравнение может быть записано в матричной форме, а некоторые геометрические свойства могут быть изучены как алгебраические условия.
На евклидовой плоскости три типа конических сечений выглядят совершенно разными, но имеют много общих свойств. Расширяя евклидову плоскость, чтобы включить в нее бесконечно удаленную линию, получая проективную плоскость , видимое различие исчезает: ветви гиперболы пересекаются в двух бесконечно удаленных точках, образуя единую замкнутую кривую; и два конца параболы встречаются, образуя замкнутую кривую, касающуюся линии на бесконечности. Дальнейшее расширение за счет расширения реальных координат до комплексных координат обеспечивает средства для алгебраического анализа этого объединения.
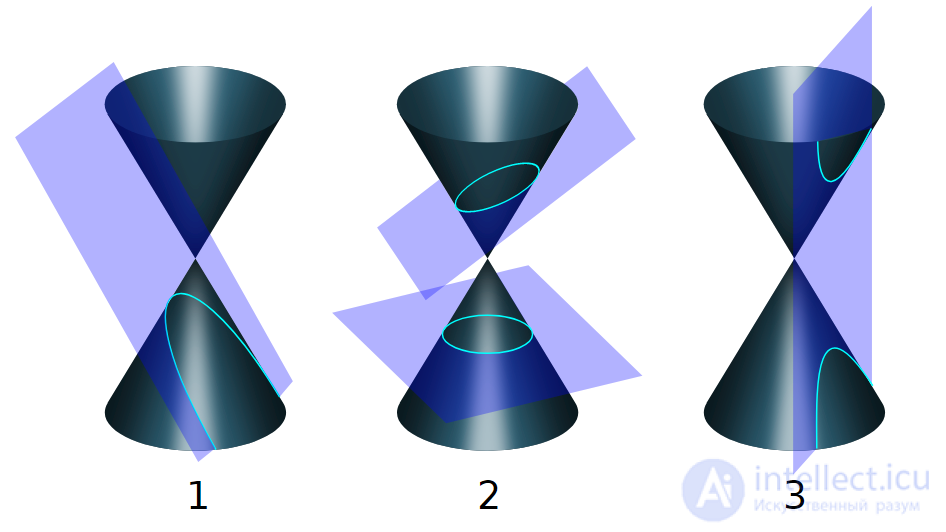
Типы конических сечений:
1. Парабола
2. Круг и эллипс
3. Гипербола.
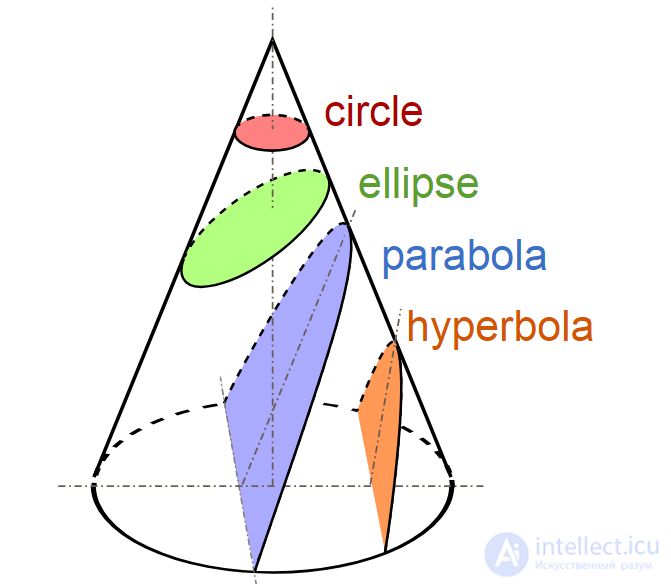
Черные границы окрашенных областей представляют собой конические участки. Не показана другая половина гиперболы, которая находится на не показанной другой половине двойного конуса.
 Таблица коников, , 1728 г.
Таблица коников, , 1728 г.Game: Perform tasks and rest cool.5 people play!
Play gameКонические сечения были известны еще математикам Древней Греции.
Наиболее полным сочинением, посвященным этим кривым, были «Конические сечения» Аполлония Пергского (около 200 г. до н. э.). По-видимому он первым описал фокусы эллипса и гиперболы :41.
Папп Александрийский первым описал фокус параболы и вывел общее уравнение для конического сечения как геометрическое место точек, для которых отношение расстояний до точки фокуса и директрисы постоянно
Считается, что первое определение конического сечения было дано Менахмом (умер в 320 г. до н.э.) как часть его решения проблемы Делиана ( Дублирование куба ). [26] [27] Его работы не сохранились, даже названия, которые он использовал для этих кривых, известны только из вторичных источников. [28] Определение, используемое в то время, отличается от того, что обычно используется сегодня. Конусы были построены путем вращения прямоугольного треугольника вокруг одного из его катетов так, чтобы гипотенуза образовывала поверхность конуса (такая линия называется образующей). Три типа конусов определялись по углам их вершин (измеренным как удвоенный угол, образованный гипотенузой и катетом, вращающимся вокруг прямоугольного треугольника). Затем определялось коническое сечение путем пересечения одного из этих конусов плоскостью, перпендикулярной образующей. Тип конуса определяется типом конуса, то есть углом, образованным в вершине конуса: если угол острый, то коника является эллипсом; если угол прямой, то коника - парабола; а если угол тупой, то коника - это гипербола (но только одна ветвь кривой). [29]
Говорят, что Евклид (около 300 г. до н. Э.) Написал четыре книги о кониках, но и они были утеряны. [30] Архимед (умер около 212 г. до н. Э.), Как известно, изучал коники, определив площадь, ограниченную параболой и хордой в квадратуре параболы . Его основной интерес был связан с измерением площадей и объемов фигур, относящихся к коникам, и часть этой работы сохранилась в его книге о телах вращения коников «О коноидах и сфероидах» . [31]
Наибольший прогресс в изучении коников древними греками был достигнут Аполлонием Пергским (умер около 190 г. до н. Э.), Чьи восьмитомные « Конические сечения» или « Коники» обобщили и значительно расширили существующие знания. [32] Изучение Аполлонием свойств этих кривых позволило показать, что любая плоскость, пересекающая фиксированный двойной конус (две вершины), независимо от ее угла, будет давать конус в соответствии с более ранним определением, что приводит к обычно используемому определению Cегодня. Таким образом также можно получить круги, которые нельзя построить предыдущим методом. Это может объяснить, почему Аполлоний считал окружности четвертым типом конического сечения, но это различие больше не проводится. Аполлоний использовал эллипс имен, парабола и гипербола для этих кривых, заимствуя терминологию из более ранних работ Пифагора о площадях. [33]
Паппу Александрийскому (умер ок. 350 г. н. Э.) Приписывают разъяснение важности концепции конического фокуса и детальное описание соответствующей концепции директрисы , включая случай параболы (которая отсутствует в известных трудах Аполлония). [34]
Инструмент для рисования конических сечений был впервые описан в 1000 году исламским математиком Аль-Кухи . [35] : 30 [36]
Работа Аполлония была переведена на арабский язык, и большая часть его работ сохранилась только в арабской версии. Персы нашли приложения теории, в первую очередь персидский [37] математик и поэт Омар Хайям , который нашел геометрический метод решения кубических уравнений с использованием конических сечений. [38] [39]
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play gameРене Декарт и Пьер Ферма применили свою недавно открытую аналитическую геометрию к изучению коник. В результате геометрические проблемы коник были сведены к задачам алгебры. Однако именно Джон Уоллис в своем трактате 1655 года Tractatus de sectionibus conicis первым определил конические сечения как примеры уравнений второй степени. [41] писалось ранее, но опубликована позже, Ян де Витт «s Elementa Curvarum Linearum начинается с Кеплера кинематическаяпостроение коник, а затем построение алгебраических уравнений. Эта работа, в которой используется методология Ферма и нотация Декарта, была названа первым учебником по этому вопросу. [42] Де Витт изобрел термин директриса . [42]
Все невырожденные конические сечения, кроме окружности, можно описать следующим способом:
Выберем на плоскости точку и прямую
и зададим вещественное число
. Тогда геометрическое место точек, для которых расстояние до точки
и до прямой {\displaystyle d}
отличается в
раз, является коническим сечением. Точка
называется фокусом конического сечения, прямая {\displaystyle d}
— директрисой, число
— эксцентриситетом.
В зависимости от эксцентриситета, получится:
Для окружности полагаю (хотя фактически при {\displaystyle e=0}
ГМТ является только точка
).
Эксцентриситет связан с параметрами конуса и расположением секущей плоскости относительно оси конуса следующим соотношением :46,47:
здесь {\displaystyle \psi } — угол наклона секущей плоскости к оси конуса,
— угол между образующей и осью конуса, равный половине угла раствора конуса. Из этой формулы видно, что, пересекая данный конус плоскостью, можно получить эллипс с любым эксцентриситетом, параболу, а гиперболу можно получить лишь такую, эксцентриситет которой не превышает
. Это максимальное значение достигается при сечении данного конуса плоскостью, параллельной его оси.
Некоторые важные свойства конических сечений получаются при рассмотрении двух шаров, касающихся конического сечения и конуса — шаров Данделена. Например, с их помощью устанавливается геометрический смысл фокуса, директрисы и эксцентриситета конического сечения :46,47.
Game: Perform tasks and rest cool.5 people play!
Play game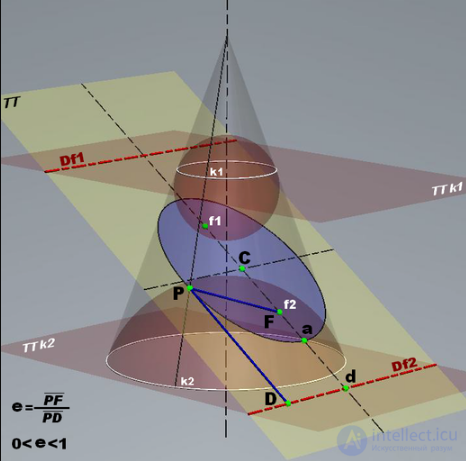
Эллипс (синий) как коническое сечение, разделяющее шары Данделена; директрисы эллипса (Df1 и Df2), его фокусы (f1 и f2) и эксцентриситет (e)
Game: Perform tasks and rest cool.5 people play!
Play game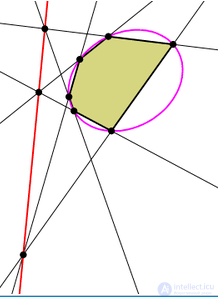 Теорема Паскаля для эллипса
Теорема Паскаля для эллипса
Зафиксируем на плоскости окружность {\displaystyle \omega }. Об этом говорит сайт https://intellect.icu . Любой точке {\displaystyle P}
плоскости можно сопоставить ее поляру {\displaystyle p}
относительно {\displaystyle \omega }
— и наоборот, любой прямой можно сопоставить ее полюс. Полученное преобразование, сопоставляющее точкам прямые, а прямым точки, называется полярным соответствием и является инволюцией, образы точек и прямых при таком преобразовании называются двойственными образами. Полярное соответствие может быть определено не только относительно окружности, но и относительно любой коники — в таком случае оно будет представлять собой композицию проективного преобразования, переводящего эту конику в окружность, полярного соответствия относительно этой окружности и обратного проективного преобразования.
Двойственным образом гладкой кривой будем называть множество двойственных образов всех касательных к этой кривой. Тогда верно, что двойственным образом коники также является коника. Таким образом, некоторые утверждения, например, теоремы Паскаля и Брианшона, являются полярно двойственными друг другу.
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play gameВ декартовых координатах, конические сечения описываются общим квадратным многочленом:
Иначе говоря, конические сечения являются кривыми второго порядка. Знак дискриминанта
определяет тип конического сечения.
В полярных координатах , с центром в одном из фокусов и нулевым направлением вдоль главной оси, коническое сечение представляется уравнением
где е обозначает эксцентриситет, а l фокальный параметр.
Конические сечения имеют некоторые очень похожие свойства в евклидовой плоскости, и причины этого становятся более ясными, когда коники рассматриваются с точки зрения более крупной геометрии. Евклидова плоскость может быть вложена в реальную проективную плоскость, а коники могут рассматриваться как объекты в этой проективной геометрии. Один из способов сделать это - ввести однородные координаты и определить конику как набор точек, координаты которых удовлетворяют неприводимому квадратному уравнению с тремя переменными (или, что эквивалентно, нулям неприводимой квадратичной формы ). Более технически, множество точек, которые являются нулями квадратичной формы (при любом количестве переменных), называется квадрикой, а неприводимые квадрики в двумерном проективном пространстве (т. е. с тремя переменными) традиционно называют кониками.
Евклидовой плоскости R 2 встраивается в вещественной проективной плоскости , примыкающая к линии на бесконечности (и его соответствующие точки на бесконечности ) , так что все линии параллельного класса встречаются на этой линии. С другой стороны, начиная с реальной проективной плоскости, евклидова плоскость получается путем выделения некоторой прямой как линии на бесконечности и удаления ее и всех ее точек.
В проективном пространстве над любым телом, но, в частности, над вещественными или комплексными числами, все невырожденные коники эквивалентны, и поэтому в проективной геометрии просто говорят о «конике», не указывая тип. То есть существует проективное преобразование, которое отображает любую невырожденную конику на любую другую невырожденную конику. [44]
Три типа конических сечений снова появятся в аффинной плоскости, полученной путем выбора прямой проекционного пространства в качестве линии на бесконечности. Затем эти три типа определяются по тому, как эта бесконечно удаленная линия пересекает конику в проективном пространстве. В соответствующем аффинном пространстве получается эллипс, если коника не пересекает линию на бесконечности, парабола, если коника пересекает прямую на бесконечности в одной двойной точке, соответствующей оси, и гипербола, если коника пересекает прямую в точке бесконечность в двух точках, соответствующих асимптотам. [45]
В однородных координатах коническое сечение можно представить в виде:
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play gameМатрица 3 × 3 выше называется матрицей конического сечения .
Некоторые авторы предпочитают записывать общее однородное уравнение в виде
(или его разновидность), так что матрица конического сечения имеет более простой вид:
но это обозначение не используется в данной статье. [46]
Если определитель матрицы конического сечения равен нулю, коническое сечение вырождено .
Поскольку умножение всех шести коэффициентов на один и тот же ненулевой скаляр дает уравнение с тем же набором нулей, можно рассматривать коники, представленные ( A , B , C , D , E , F ), как точки в пятимерной проективной проекции. Космос
Метрические концепции евклидовой геометрии (концепции, связанные с измерением длины и углов) не могут быть немедленно распространены на реальную проективную плоскость. [47] Они должны быть переопределены (и обобщены) в этой новой геометрии. Это можно сделать для произвольных проективных плоскостей , но чтобы получить реальную проективную плоскость в качестве расширенной евклидовой плоскости, необходимо сделать определенный выбор. [48]
Зафиксируем произвольную прямую на проективной плоскости, которую мы будем называть абсолютной прямой . Выберите две различные точки на абсолютной линии и назовите их абсолютными точками . Со ссылкой на эти варианты можно определить несколько метрических концепций. Так , например, учитывая строку , содержащую точки A и B , то средняя точка отрезка линии AB определяется как точка C , которая является гармоническая четверка точки пересечения AB и абсолютной линии, по отношению к A и B .
Коника на проективной плоскости, содержащая две абсолютные точки, называется окружностью . Поскольку пять точек определяют конику, окружность (которая может быть вырожденной) определяется тремя точками. Чтобы получить расширенную евклидову плоскость, абсолютная линия выбирается как бесконечно удаленная от евклидовой плоскости, а абсолютные точки - это две особые точки на этой прямой, называемые круговыми точками на бесконечности . Линии, содержащие две точки с действительными координатами, не проходят через круглые точки на бесконечности, поэтому в евклидовой плоскости круг, согласно этому определению, определяется тремя точками, которые не лежат на одной прямой . [49] : 72
Было упомянуто, что окружности в евклидовой плоскости не могут быть определены свойством фокус-директрисы. Однако, если рассматривать линию на бесконечности как направляющую, тогда, если принять эксцентриситет равным e = 0, круг будет обладать свойством фокус-направляющей, но по-прежнему не определяется этим свойством. [50] В этой ситуации нужно быть осторожным, чтобы правильно использовать определение эксцентриситета как отношение расстояния от точки на окружности до фокуса (длина радиуса) к расстоянию от этой точки до направляющей (это расстояние бесконечно), что дает нулевое предельное значение.
Синтетический (бескоординатный) подход к определению конических сечений в проективной плоскости был дан Якобом Штайнером в 1867 году.
Перспективное отображение карандаша
на карандаш
является взаимно однозначным соответствием (1-1 переписки) таким образом, что соответствующие линии пересекаются на фиксированную линии
, которая называется осью перспективности
.
Проективное отображение является конечной последовательностью перспективных отображений.
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play game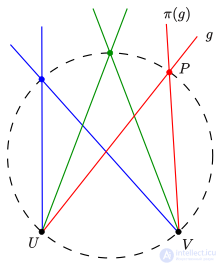
Определение генерации Штейнера конического сечения
Согласно принципу двойственности на проективной плоскости двойственная точка каждой точки является линией, а двойственная точка множества точек (набор точек, удовлетворяющих некоторому условию) называется оболочкой прямых. Используя определение Штейнера коники (это множество точек теперь будем называть точечной коникой ) как пересечения соответствующих лучей двух связанных пучков, легко дуализировать и получить соответствующую оболочку, состоящую из стыков соответствующих точек два связанных диапазона (точки на линии) на разных основаниях (линии, на которых находятся точки). Такая оболочка называется прямой конической (или дуальной конической ).
В реальной проективной плоскости точечная коника обладает тем свойством, что каждая прямая пересекает ее в двух точках (которые могут совпадать или могут быть комплексными), и любой набор точек с этим свойством является точечной коникой. Отсюда вдвойне следует, что у прямой коники есть две прямые, проходящие через каждую точку, и любая огибающая прямых с этим свойством является прямой конической. В каждой точке точечной коники есть уникальная касательная линия, и, вдвойне, на каждой прямой конической прямой есть единственная точка, называемая точкой контакта . Важная теорема утверждает, что касательные линии точечной коники образуют прямую конику, а точки соприкосновения прямой коники образуют коническую точку. [56] : 48–49
Карл Георг Христиан фон Штаудт определил конику как точку, заданную всеми абсолютными точками полярности, которая имеет абсолютные точки. Фон Штаудт ввел это определение в Geometrie der Lage (1847) как часть своей попытки удалить все метрические концепции из проективной геометрии.
Полярности , π , проективная плоскость, Р , является инволютивной (т.е. порядка два) биекции между точками и линиями Р , сохраняющее соотношением инцидентности . Таким образом, полярность относится точка Q с линией ц и, после Gergonne , д называется полярный из Q и Q полюс из ц . [57] абсолютная точка ( линия ) от полярности один , который падает с его полярным (полюсом).[58]
Коника фон Штаудта в вещественной проективной плоскости эквивалентна конике Штейнера . [59]
Невозможно построить непрерывную дугу коники с помощью линейки и циркуля. Однако существует несколько построений линейки и циркуля для любого количества отдельных точек на дуге.
Один из них основан на обратной теореме Паскаля, а именно, если точки пересечения противоположных сторон шестиугольника лежат на одной прямой, то шесть вершин лежат на конике. В частности, из пяти точек A , B , C , D , E и прямой, проходящей через E , скажем EG , \ можно построить точку F, которая лежит на этой прямой и находится на конике, определяемой этими пятью точками. Пусть AB пересекает DE в L , BC пересекает EG в M и пусть CD пересекаетLM наN. Тогдасоответствует EG в нужной точкеF. [60] : 52–53 Изменяя прямую, проходящую черезE, можно построить сколько угодно дополнительных точек на конике.
Другой метод, основанный на конструкции Штейнера и полезный в инженерных приложениях, - это метод параллелограмма , при котором коника строится точка за точкой путем соединения определенных равноотстоящих точек на горизонтальной и вертикальной линиях. [61] В частности, чтобы построить эллипс с помощью уравнениях 2/а 2 + y 2/б 2= 1 , сначала построим прямоугольник ABCD с вершинами A ( a , 0), B ( a , 2 b ), C (- a , 2 b ) и D (- a , 0) . Разделите сторону BC на n равных отрезков и используйте параллельную проекцию относительно диагонали AC , чтобы сформировать равные отрезки на стороне AB (длины этих отрезков будут равныб/аумноженное на длину отрезков BC ). На стороне BC этикетке левой концы отрезков с А 1 до А п , начиная с B и происходит в направлении C . На стороне АВ маркировать верхние конечные точки D 1 до D п , начиная с А и происходит в направлении B . Точки пересечения AA i ∩ DD i для 1 ≤ i ≤ n будут точками эллипса между A иР (0, б ) . Маркировка связывает линии карандаша черезточку A с линиями карандаша черезточку D проективно, но не в перспективе. Искомая коника получается с помощью этой конструкции, поскольку три точки A , D и P и две касательные (вертикальные прямые вточках A и D) однозначно определяют конику. Если другой диаметр (и сопряженный к нему диаметр) используется вместо большой и малой осей эллипса, в конструкции используется параллелограмм, который не является прямоугольником, давая имя методу. Объединение линий карандашей может быть расширено, чтобы получить другие точки на эллипсе. Аналогичны конструкции для гипербол [62] и парабол [63] .
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play gameВ комплексной плоскости C 2 эллипсы и гиперболы не различимы: можно рассматривать гиперболу как эллипс с мнимой длиной оси. Например, эллипс становится гиперболой при замене
геометрически сложное вращение, дающее
. Таким образом, существует двухсторонняя классификация: эллипс / гипербола и парабола. Продолжение кривых до комплексной проективной плоскости соответствует пересечению бесконечно удаленной прямой в двух различных точках (соответствующих двум асимптотам) или в одной двойной точке (соответствующей оси параболы); таким образом, реальная гипербола является более убедительным реальным изображением для сложного эллипса / гиперболы, поскольку она также имеет 2 (реальных) пересечения с линией на бесконечности.
Дальнейшее объединение происходит в комплексной проективной плоскости CP 2 : невырожденные коники нельзя отличить друг от друга, так как любая может быть переведена в любую другую проективным линейным преобразованием .
Можно доказать, что в CP 2 два конических сечения имеют четыре общие точки (если учесть множественность ), так что имеется от 1 до 4 точек пересечения . Возможны следующие варианты пересечения: четыре различные точки, две особые точки и одна двойная точка, две двойные точки, одна особая точка и одна с кратностью 3, одна точка с кратностью 4. Если любая точка пересечения имеет кратность> 1, две кривые называются быть касательным . Если имеется точка пересечения с кратностью не менее 3, две кривые называются соприкасающимися . Если имеется только одна точка пересечения, кратность которой равна 4, две кривые называются сверхскоростными .[65]
Кроме того, каждая прямая линия дважды пересекает каждый конический участок. Если точка пересечения двойная, линия представляет собой касательную . Каждая коническая секция, пересекающаяся с бесконечно удаленной линией, имеет две бесконечно удаленные точки. Если эти точки действительны, кривая представляет собой гиперболу ; если они воображаемые конъюгаты, это эллипс ; если есть только одна двойная точка, это парабола . Если бесконечно удаленные точки являются циклическими точками (1, i , 0) и (1, - i , 0) , коническое сечение представляет собой окружность . Если коэффициенты конического сечения действительны, бесконечно удаленные точки либо действительны, либокомплексно-сопряженный .
То, что следует рассматривать как вырожденный случай коники, зависит от используемого определения и геометрических параметров конического сечения. Некоторые авторы определяют конику как двумерную невырожденную квадрику. В этой терминологии нет вырожденных коник (только вырожденные квадрики), но мы будем использовать более традиционную терминологию и избегать этого определения.
В евклидовой плоскости, используя геометрическое определение, возникает вырожденный случай, когда секущая плоскость проходит через вершину конуса. Вырожденная коника - это либо: точка , когда плоскость пересекает конус только на вершине; прямая линия , когда плоскость является касательной к конусу (он содержит ровно один генератор конуса); или пара пересекающихся прямых (две образующие конуса). [66] Они соответствуют предельным формам эллипса, параболы и гиперболы соответственно.
Если коника на евклидовой плоскости определяется нулями квадратного уравнения (то есть как квадрика), то вырожденными кониками являются: пустое множество , точка или пара прямых, которые могут быть параллельны, пересекаются в точке или совпадают. Случай пустого множества может соответствовать либо паре комплексно сопряженных параллельных прямых, например, уравнениюили воображаемому эллипсу , например, с уравнением
Мнимый эллипс не удовлетворяет общему определению вырождения и, следовательно, обычно не считается вырожденным. [67] Случай двух линий возникает, когда квадратное выражение делится на два линейных множителя, нули каждого из которых дают линию. В случае, если коэффициенты одинаковы, соответствующие прямые совпадают, и мы называем эту линию двойной линией (линия с кратностью 2), и это предыдущий случай касательной плоскости сечения.
В реальной проективной плоскости, поскольку параллельные прямые пересекаются в точке на бесконечности, случай параллельной прямой евклидовой плоскости можно рассматривать как пересекающиеся прямые. Однако, поскольку точка пересечения является вершиной конуса, сам конус вырождается в цилиндр , то есть с вершиной на бесконечности. Остальные секции в этом случае называются цилиндрическими секциями . [68] Невырожденные цилиндрические секции представляют собой эллипсы (или окружности).
Если смотреть с точки зрения комплексной проективной плоскости, вырожденные случаи реальной квадрики (т. Е. Квадратное уравнение имеет действительные коэффициенты) можно рассматривать как пару прямых, возможно совпадающих. Пустым набором может быть линия на бесконечности, рассматриваемая как двойная линия, (действительная) точка - это пересечение двух комплексно сопряженных линий и других случаев, как упоминалось ранее.
Game: Perform tasks and rest cool.5 people play!
Play gameGame: Perform tasks and rest cool.5 people play!
Play game(Невырожденная) коника полностью определяется пятью точками общего положения (без трех коллинеарных ) на плоскости, и система коник, которые проходят через фиксированный набор из четырех точек (опять же на плоскости, а не трех коллинеарных), называется пучок коник . [70] : 64 Четыре общие точки называются базовыми точками карандаша. Через любую точку, кроме базовой, проходит единственный конус карандаша. Это понятие обобщает пучок окружностей . [71] : 127
Решения системы двух уравнений второй степени с двумя переменными можно рассматривать как координаты точек пересечения двух конических сечений общего положения. В частности, две коники могут не иметь ни одной, двух или четырех возможно совпадающих точек пересечения. Эффективный метод поиска этих решений использует однородное матричное представление конических сечений , то есть симметричную матрицу 3x3, которая зависит от шести параметров.
Процедура определения точек пересечения состоит из следующих шагов, где коники представлены матрицами: [72]
Коники могут быть определены над другими полями (то есть в других папповых геометриях ). Однако следует проявлять некоторую осторожность, когда поле имеет характеристику 2, поскольку некоторые формулы нельзя использовать. Например, используемые выше матричные представления требуют деления на 2.
Обобщением невырожденной коники на проективной плоскости является овал . Овал - это набор точек, который обладает следующими свойствами, которые поддерживаются кониками: 1) любая прямая пересекает овал ни в одной, одной или двух точках, 2) в любой точке овала существует единственная касательная линия.
Обобщение свойств фокуса коник на случай, когда имеется более двух фокусов, дает наборы, называемые обобщенными кониками .
Классификация на эллиптические, параболические и гиперболические широко распространена в математике и часто делит поле на четко определенные подполя. Классификация в основном возникает из-за наличия квадратичной формы (в двух переменных это соответствует ассоциированному дискриминанту ), но также может соответствовать эксцентриситету.
Классификация квадратичных форм:
Квадратичные формы
Квадратичные формы над вещественными числами классифицируются по закону инерции Сильвестра , а именно по их положительному, нулевому и отрицательному индексам: квадратичная форма от n переменных может быть преобразована в диагональную форму , какгде число коэффициентов +1, k, является положительным индексом, количество коэффициентов −1 ,, является отрицательным индексом, а остальные переменные представляют собой нулевой индекс m, поэтому
В двух переменных ненулевые квадратичные формы классифицируются как:
Game: Perform tasks and rest cool.5 people play!
Play gameКривизна
Гауссова кривизна из поверхности описывает геометрию бесконечно малого, и может в каждой точке быть либо положительным - эллиптическая геометрия , нулевой - геометрия Евклида (плоская, парабола), или отрицательными - гиперболические геометрии ; бесконечно мало, до второго порядка поверхность выглядит как график
(или 0), или
. В самом деле, по теореме униформизации любую поверхность можно считать глобально (в каждой точке) положительно изогнутой, плоской или отрицательно изогнутой. В более высоких измерениях тензор кривизны Римана представляет собой более сложный объект, но многообразия с постоянной секционной кривизной являются интересными объектами изучения и обладают совершенно разными свойствами, как обсуждалось при секционной кривизне .
PDE второго порядка
Уравнения с частными производными (УЧП) второго порядка классифицируются в каждой точке как эллиптические, параболические или гиперболические, соответственно, поскольку их члены второго порядка соответствуют эллиптической, параболической или гиперболической квадратичной форме. Поведение и теория этих различных типов УЧП разительно различаются - характерным примером является то, что уравнение Пуассона является эллиптическим, уравнение теплопроводности - параболическим, а волновое уравнение - гиперболическим.
Классификация эксцентриситета включает:
Преобразования Мебиуса
Реальные преобразования Мебиуса (элементы PSL 2 ( R ) или его 2-кратного покрытия, SL 2 ( R ) ) классифицируются как эллиптические, параболические или гиперболические соответственно, поскольку их полуслед
или
зеркальное отображение классификации по эксцентриситету.
Отношение дисперсии к среднему
Отношение дисперсии к среднему классифицирует несколько важных семейств дискретных распределений вероятностей : постоянное распределение как круговое (эксцентриситет 0), биномиальные распределения как эллиптические, распределения Пуассона как параболические и отрицательные биномиальные распределения как гиперболические. Это разрабатывается в кумулянтах некоторых дискретных распределений вероятностей .
Конические сечения важны в астрономии : орбиты двух массивных объектов, которые взаимодействуют согласно закону всемирного тяготения Ньютона, являются коническими сечениями, если их общий центр масс считается покоящимся. Если они связаны вместе, они оба начертят эллипсы; если они расходятся, они оба будут следовать параболам или гиперболам. См. Проблему двух тел .
Отражающие свойства конических секций используются в конструкции прожекторов, радиотелескопов и некоторых оптических телескопов. [43] В прожекторах в качестве отражателя используется параболическое зеркало с лампочкой в фокусе; и аналогичная конструкция используется для параболического микрофона . В оптическом телескопе Herschel размером 4,2 метра на Ла-Пальме, на Канарских островах, используется первичное параболическое зеркало, чтобы отражать свет во вторичное гиперболическое зеркало, которое снова отражает его в фокус за первым зеркалом.
В рамках классической механики траектория движения материальной точки или жесткого сферически симметричного тела в поле силы, подчиняющейся закону обратных квадратов, является одним из конических сечений — параболой, гиперболой, эллипсом (в частности кругом) или прямой. В случае, когда такая сила является силой притяжения, возможны (в зависимости от начальных условий) все эти траектории, если же это сила отталкивания, то возможны только прямые и гиперболы.
Траектория движения тела (или его центра массы в случае любого неточечного тела) в поле однородной постоянной силы в рамках классической механики - точная парабола.
Game: Perform tasks and rest cool.5 people play!
Play gameФизически ситуация может относится как к взаимодействию точечных (имеющих очень малый размер по сравнению с расстоянием до других тел) или сферических тел под действием сил гравитации, подчиняющихся закону всемирного тяготения (этот закон является довольно хорошим приближенным описанием реального гравитационного взаимодействия в большинстве случаев, с которыми мы сталкиваемся в пределах Солнечной системы) и/или электростатических сил, подчиняющихся закону Кулона .
Для того, чтобы траектории тел были коническими сечениями важно, чтобы соблюдались условия на количество и/или массы взаимодействующих тел, описанные выше, а также чтобы в идеале отсутствовали (практически же были пренебрежимо малыми, или, иногда, хорошо скомпенсированными) все другие силы, как например силы аэродинамического сопротивления (для этого, например, нужен достаточная разреженность среды, вакуум), потери на излучение (в случае движения электрически заряженных тел они могут быть существенны, в рамках ньютоновской гравитации такие потери всегда равны нулю, однако в реальности потери на излучение гравитационных волн могут быть заметны при взаимодействии близких массивных и быстро движущихся объектов). Кроме обычного аэродинамического сопротивления могут быть существенными такие силы, как сила давления и сила сопротивления, обусловленные солнечным ветром. При движении космических тел, как правило, эти условия выполняются по крайней мере в какой-то степени, так что коническое сечение является приемлемым, а часто и очень хорошим, приближением реальной орбиты (в течение какого-то времени).
В Солнечной системе орбиты планет — с достаточно хорошим приближением эллипсы (отклонение от точной эллиптичности больше всего у Меркурия), траектории комет — эллипсы, гиперболы[10] нередко траектории комет «почти параболические»[11] (см. также Небесная механика). Траектория полета пушечного ядра в гравитационном поле Земли без учета влияния воздуха — дуга эллипса близкого к параболе (поскольку скорость ядра гораздо меньше первой космической).
В небольшой (по сравнению с радиусом Земли) лаборатории гравитационное поле можно считать однородным постоянным. Если в такой лаборатории достаточно хорошо откачать воздух, то траектория камня, брошенного в ней, будет практически точной параболой (или прямой)[12]. При обычных условиях (присутствие воздуха) траектории брошенных тел вообще говоря достаточно сильно отличаются от парабол и прямых (за исключением строго вертикального броска), однако при малых скоростях и небольших расстояниях полета могут быть довольно близки к параболе.
Древние греки занимались изучением эллипса, гиперболы и параболы, рассматривая их как конические сечения. Аполлоний (262 до н. э. — 190 до н. э., родом из Перги, но работавший в Александрии, современник Архимеда) написал труд «Конические сечения» в восьми книгах, половина из которых дошла до наших дней только в средневековых арабских переводах.
Аполлоний рассматривал фокусы эллипса и гиперболы, хотя у него и не было специального термина для этих точек, знал их свойства, включая оптические.
Диокл, младший современник Аполлония, в сочинении «О зажигательных зеркалах» приводит оптическое свойство параболы, видимо, основываясь на результатах ученых круга Архимеда. Это сочинение также сохранилось лишь благодаря арабским переводам, в которых параболоид вращения назывался «зажигательным зеркалом», а фокус параболы — «местом зажигания».
При издании латинских переводов арабских математических текстов «место зажигания» не могло не превратиться в латинское focus — «очаг, огонь». Как термин «фокус» был введен Иоганном Кеплером в сочинении «Оптическая часть астрономии» («Astronomiae pars optica», 1604), причем не только для параболы, но и для эллипса и гиперболы.
Game: Perform tasks and rest cool.5 people play!
Play gameОптическое свойство параболы предстанет как экспериментальный факт, если изготовить параболический бильярд.
В этой модели изогнутый бортик представляет параболу, на сукне отмечен фокус — точка, в которую надо поставить шарик‐мишень. Основной шарик будет скатываться с подвижной горки, которую всегда размещают так, чтобы направление скатывающегося шарика было параллельно оси параболы (например, можно сдвигать горку вдоль прямой стенки бильярда, расположенной перпендикулярно оси параболы). Шарик, скатываясь с горки, после отражения от бортика всегда будет попадать в шарик, размещенный в фокусе параболы!

При самостоятельном изготовлении модели следует учесть, что бортик — это эквидистанта параболы, ее сдвиг в каждой точке по нормали к параболе на расстояние, равное радиусу шарика (в идеальной геометрической модели от параболы отражается центр шарика, точка). Радиус шарика должен быть не слишком мал, чтобы сглаживать возможные погрешности.
Качество изготовленной модели можно оценить, если провести эксперимент, убрав шарик‐мишень. Скатывающийся с горки шарик после первого отражения от бортика должен пройти через отмеченный фокус, а после второго — покатиться параллельно оси параболы.
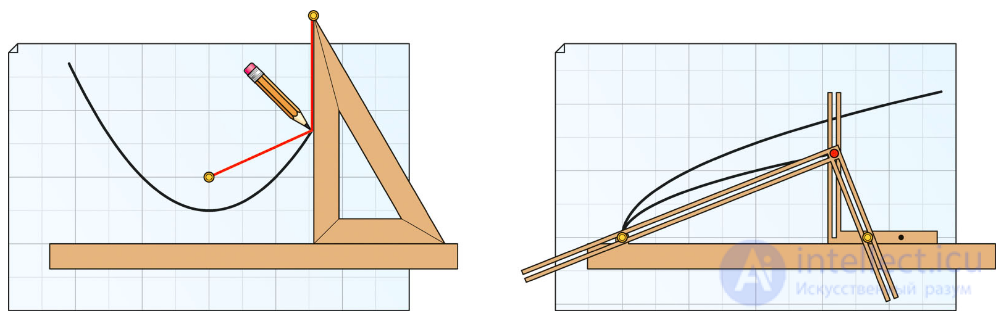
Геометрическое определение позволяет нарисовать параболу с данным фокусом и данной директрисой.
Вдоль директрисы положим линейку, в фокусе кнопкой закрепим конец нити. Второй конец нити закрепляется в вершине угольника, катет которого приложен к линейке. Если прижать нить ко второму катету карандашом, сохраняя ее натянутой при скольжении угольника вдоль линейки, то проведенная линия будет параболой.
Устройства, вычерчивающие параболы, называются параболографами. Изящную конструкцию придумал в XVII веке итальянский математик Бонавентура Кавальери (известный как предшественник создателей интегрального исчисления).
Устройство состоит из трех связанных деталей: неподвижной относительно листа линейки (горизонталь) и двух жестких прямых углов. У первого угла горизонтальная сторона скользит вдоль линейки, а по его вертикальной стороне скользит вершина (с грифелем) второго угла. При этом в каждый момент времени стороны второго угла проходят через штифты: один закреплен на неподвижной линейке, а другой — на горизонтальной стороне подвижного угла.
То, что линия, проведенная грифелем, будет параболой, следует из известного свойства прямоугольного треугольника: квадрат длины высоты, опущенной на гипотенузу, равен произведению длин отрезков, на которые ее делит высота. Параметр параболы регулируется перемещением штифта на горизонтальной стороне первого угла.
Параболу можно «изготовить», проведя серию опытов с бумажным листом — в результате вы получите не нарисованную, но «видимую» линию, которой касаются многочисленные прямые.
На листе бумаги нарисуйте прямую и отметьте точку, не лежащую на этой прямой (фокус будущей параболы). Через выбранную точку на прямой проведите перпендикуляр к отрезку, соединяющему эту точку с отмеченной. Перпендикуляр можно даже не проводить карандашом, а определить на глаз и перегнуть по нему лист бумаги. Проделав процедуру для нескольких точек на прямой, вы увидите параболу, как границу области, «окруженной» линиями сгиба.
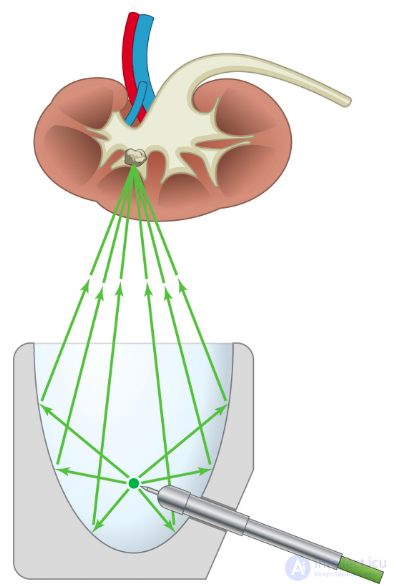
Как огибающую семейства линий (см. Болтянский В. Г. «Огибающая») можно получить и другие конические сечения , только вместо начальной прямой нужно взять окружность. Если точка (фокус) внутри окружности, то получится эллипс (см. «Дробление камней в почках»); если снаружи — гипербола (см. «Шуховские башни»).

Все конические сечения (эллипс, параболу, гиперболу) можно получить в виде муара — дополнительного геометрического узора, образующегося при наложении двух изображений.
Возьмите «прозрачку» и на принтере напечатайте прямолинейные полоски на фиксированном расстоянии между соседними. На другом листе напечатайте круговые полоски (концентрические окружности) той же ширины и с тем же расстоянием между соседними.
Если наложить эти листы друг на друга так, чтобы одна из прямых проходила через центр окружностей, то вы увидите семейство парабол. А если наложить две одинаковые «круговые» прозрачки так, чтобы расстояние между центрами кругов было кратно расстоянию между окружностями, то можно увидеть эллипсы и пересекающие их гиперболы.
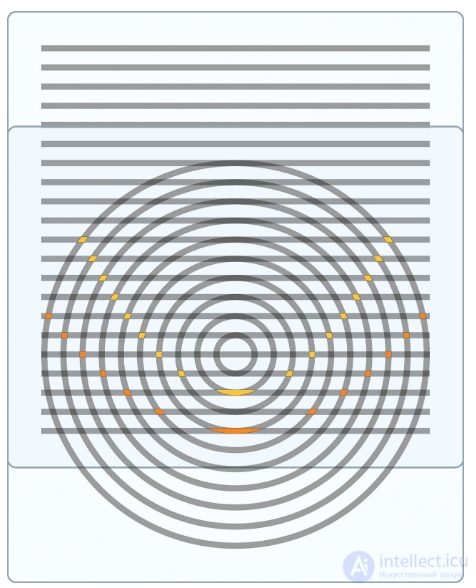

Game: Perform tasks and rest cool.5 people play!
Play gameЧитатель мог встречать впечатляющую игрушку: на крышке «летающей тарелки» вы видите объект, осязаемо‐объемный, пытаетесь его взять, и… пальцы встречают пустоту. Это иллюзорный объект, а его «появление» — результат оптического свойства параболы.
Игрушка состоит из двух соосных параболоидов вращения, чаши которых обращены друг к другу, шапочка верхней чаши срезана. На нижней чаше, в фокусе верхнего параболоида находится объект; после отражений в зеркальных стенках параболоидов в фокусе нижнего формируется изображение.

Исаак Ньютон заметил, что при вращении цилиндрического сосуда поверхность налитой в него жидкости принимает форму параболоида, и объяснил это явление с помощью найденных им самим законов.
В наше время этот эффект используют при изготовлении больших параболических зеркал для телескопов — этот способ быстрее и дешевле, чем классическая шлифовка. А иногда создают и «временные» телескопы с жидким зеркалом: сосуд с ртутью вращают только во время проведения наблюдений.
«Параболическими» являются такие альпийские и арктические цветы, как прострел альпийский, беквичия ледниковая, полярный мак. Благодаря оптическому свойству параболы у таких цветов ускоряется созревание семян. Еще одно полезное для цветов следствие их параболичности — привлечение насекомых, которые любят «понежиться» в чаше цветка, а это влияет на опыление.
Если на параболе по разные стороны от оси взять точки и , то соединяющий их отрезок пересечет ось в точке . Первым это отметил Август Мебиус, имя которого носит знаменитая односторонняя лента.
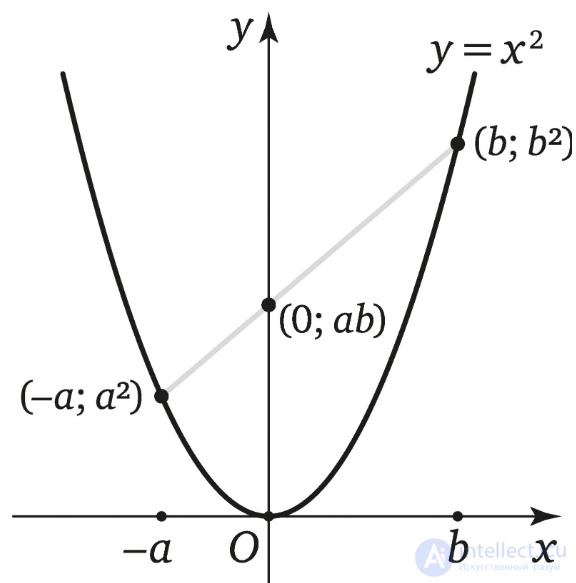

Можно взглянуть на этот факт и с другой стороны: через точку , где — составное число, проходит хорда параболы описанного вида ( и — натуральные числа, отличные от 1). А через точку вида , где — простое число, не проходит ни одна подобная хорда.
Это замечание можно превратить в алгоритм, позволяющий найти все простые числа до некоторого : «параболическое решето», отсеивающее все составные числа.
Исследование, описанное в статье про коническое сечение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое коническое сечение, коника и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия