Лекция
Привет, Вы узнаете о том , что такое фигуры четырехмерного пространства, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое фигуры четырехмерного пространства, дуопризма, дуоцилиндр, гиперсфера, бутылка клейна, гиперконус, тор клиффорда, гиперкуб, многогранник дюрера , настоятельно рекомендую прочитать все из категории Стереометрия.
Сегодня каждому обучающемуся известно, что пространство, в котором существует человек, трехмерно, то есть у него имеется три измерения: длина, ширина и высота. Но что такое четырехмерное пространство? Если мы будем исследовать не только пространственное положение тела, но и то, как оно изменяется во времени, то есть процессы, которые происходят в трехмерном пространстве, появляется еще одна координата – время. Четырехмерное пространство и состоит из трех пространственных и одной временной координаты. В этом случае физики и философы говорят о единстве пространства и времени. Время и пространство взаимосвязаны между собой. По существу, они проявляются как различные стороны четырехмерного пространства-времени.
Людвиг Шлефли один из первых выдвинул идею о том, что даже если наше физическое пространство имеет размерность 3, то ничто не может помешать нам представлять себе пространство размерности 4, или даже доказывать геометрические теоремы о четырехмерных математических объектах.
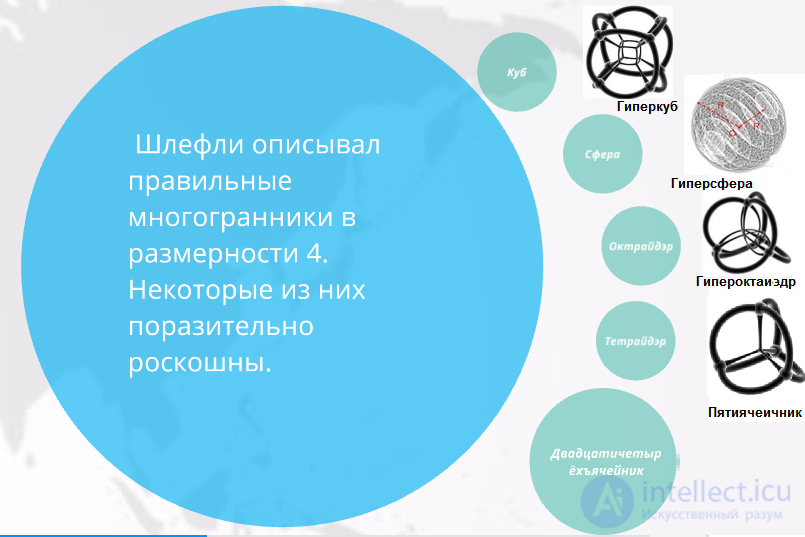
Первый метод — наиболее прагматичный. Мы можем просто сказать, что точка в четырехмерном пространстве — это просто набор данных, состоящий из четырех чисел: x, y, z, t. Недостаток данного подхода в том, что так трудно что-нибудь представить визуально. Но он вполне логичен и большинство математиков довольствуется им.
Вторым Шлефли дает нам объяснение "по аналогии". Идея заключается в том, чтобы внимательно рассмотреть размерности 1, 2 и 3, заметить некоторые явления, а затем предположить, что эти явления есть и в четвертом измерении.
Особенности нашего восприятия мира.
Когда мы в школе рисовали плоские геометрические фигуры, то не испытывали никаких особых затруднений – они были двумерны (имели ширину и длину). Сложнее было рисовать и представлять трехмерные фигуры – конусы, пирамиды, цилиндры и другие. А вообразить четырехмерные фигуры довольно трудно даже математикам и физикам. Конечно, к понятию «четырехмерное пространство» необходимо привыкнуть. Причина тут не психологическая, а чисто физиологическая. Все дело в устройстве наших глаз. Когда мы смотрим на удаленный предмет, особые мускулы изгибают хрусталик глаза – естественную линзу, чтобы изменить ее фокусное расстояние и дать нам увидеть предмет отчетливо. И еще в каждом глазе есть группа из шести мускулов, которые поворачивают его таким образом, чтобы направления взгляда правого и левого глаза пересекались в одной точке. Это называется конвергенцией. Так создается бинокулярный эффект – мы видим мир объемным. Человечество пошло не по пути овладения третьим измерением, а по пути его «приручения»: люди старались втиснуть объем в плоскость, изобразить окружающий мир на скале, песке или папирусе.
Вся беда в том, что мы сами живем в третьем измерении и поэтому смотрим на него «изнутри», наш объемный мир мы видим как бы плоским. Звучит парадоксально, но поместите лист бумаги с нарисованной на нем фигурой точно на уровне глаз – и вы на секунду испытаете трагедию людей, обреченных жить в двух измерениях, но ощущать лишь одно. Ведь чтобы увидеть фигуру – квадрат ли, круг, надо хоть немного «выскочить» из своей плоскости.
Особенности четырехмерного пространства.
Нарисуйте на плоскости круг и представьте себя в виде воображаемого существа двумерного мира, которое может двигаться по плоскости, но не имеет права выходить в пространство. (Вы даже не знаете, что пространство существует, и не можете его вообразить.) Тогда граница круга — окружность — будет для вас непреодолимой преградой: вы не сможете выйти из круга, ибо окружность будет всюду преграждать вам путь.
Теперь представьте, что эта плоскость с нарисованным кругом помещена в трехмерное пространство и что вы догадались о существовании третьего измерения. Теперь вы, конечно, без труда выйдете за пределы круга, например просто перешагнете через окружность.
Пусть теперь вы — существо трехмерного мира. Пусть вы находитесь внутри шара, граница которого (сфера) для вас непроходима. Тогда вы не сможете выйти за пределы этого шара. Но если шар помещен в четырехмерное пространство и вы догадались о существовании четвертого измерения, то вы без всяких усилий сможете выйти за пределы шара.
Ничего особенно мистического в этом нет — просто граница трехмерного шара (сфера) не разбивает четырехмерного пространства на две части, хотя трехмерное пространство она разбивает. Это вполне аналогично тому, что граница круга (окружность) не разбивает трехмерного пространства на две части, хотя плоскость (в которой она лежит) эта окружность разбивает.
Еще один пример: ясно, что две симметричные друг другу фигуры на плоскости нельзя совместить, если их разрешается лишь перемещать, не выводя из плоскости. Однако сидящая бабочка может сложить крылья, выводя их из горизонтальной плоскости в вертикальную. Так же и в пространстве трех измерений нельзя совместить симметричные пространственные фигуры. Например, как ни верти, левую перчатку нельзя превратить в правую, хотя они являются равными геометрическими фигурами. А в пространстве четырех измерений трехмерные симметричные фигуры можно совместить подобно тому, как плоские симметричные фигуры совмещаются, если их вывести в трехмерное пространство.
Поэтому нет ничего удивительного в том, что герой выше упомянутого рассказа Уэллса после своего путешествия в четырехмерное пространство оказался перевернутым, симметричным самому себе: сердце у него, например, оказалось справа. Это произошло потому, что, выйдя в четырехмерное пространство, он вывернулся в нем на другую сторону (подобно тому, как левая перчатка, вывертываясь наизнанку, превращается в правую).
Все очень просто. 0D измерение - точка. 1D измерение - прямая. 2D -измерение - плоскость. К плоскости прибавим высоту - получим 3D- измерение - объем. К привычным нам длине-ширине-высоте (3D) добавляется еще одна ось или четвертое измерение- объем просматривается со всех сторон и изнутри в динамичном виде.
3.1.Четырехмерный симплекс
Симплекс (простейший) — это простейшая из всех возможных фигур имеет 5 вершин, 10 граней, 10 ребер,5 тетраграней. Эта необычная конструкция состоит из пяти пирамид. Все вместе они отделяют четырехмерный симплекс от остального четырехмерного пространства точно так же, как шесть граней куба отделяют его от остального трехмерного пространства, а три стороны треугольника ограничивают его на плоскости.
3.2.Тессеракт ( гиперкуб )
Четырехмерный аналог обычного нашего 3-мерного куба известен под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.
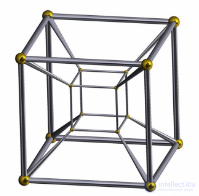
Каждая пара непараллельных трехмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трехмерными гранями, 24 двумерными, 32 ребрами и 16 вершинами.
Но что подтверждает, что гиперкуб не принадлежит к нашему трехмерному миру? Существует один простой тест, основанный на формуле, выведенной еще Леонардом Эйлером для любой геометрической трехмерной фигуры.
Вот она: Г + В = Р + 2. То есть число граней (Г) плюс число вершин (В) равно числу ребер (Р) плюс 2. Проверьте правильность этой формулы на какой угодно фигуре — кубе, пирамиде, тетраэдре, икосаэдре, произвольном многограннике, теле самой замысловатой формы. При любых деформациях любой из них формула Эйлера верна. Но возьмите гиперкуб. 24 стороны, 16 вершин, 32 ребра и сверх того 8 трехмерных граней — вот то геометрическое богатство, которым он обладает. Простейшие арифметические действия убедят вас, что гиперкуб пришел к нам в гости из сложнейшего четырехмерного мира, для него несправедлива формула Эйлера.
многогранник дюрера — многогранник, изображенный на гравюре «Меланхолия I», работе художника Альбрехта Дюрера, датируемой 1514 годом. Эта яркая деталь гравюры «Меланхолия I» дала название для геометрической фигуры. Точная геометрия этого тела является предметом незаконченных научных споров и источником вдохновения для современных художников.Форма монолита, изображенного Дюрером, является предметом незаконченных академических дебатов. Существует гипотеза, что это усеченный куб, но большинство источников согласны, что это усечение ромбоэдра.
Существует также предположение что это трехерное сечение(что что видно в техмерном пространстве) четырехмерного куба в техмерном пространстве.


3.2.1.Построение и описание гиперкуба
Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трехмерного пространства. Возьмем проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединенные четырьмя линиями — боковыми ребрами.
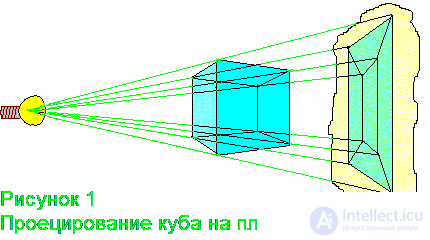
А что мы делаем, чтобы изобразить на плоском листе бумаге трехмерный куб? Мы проецируем его на плоскость. Получается два квадрата один в другом, соединенные вершинами (рис. 1).
Так же спроецируем и четырехмерный куб. Мы получим по аналогии два куба, один в другом, и снова вершины попарно соединены. Вот он, посланец четвертого измерения, вернее, не сам он, а его проекция на плоскость (Рис. 2).
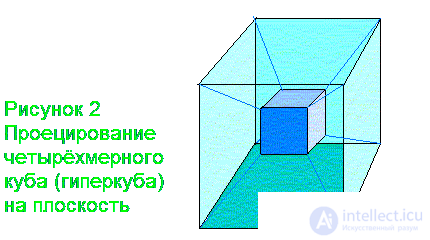
Четырехмерный гиперкуб в пространстве трех измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединенных восемью ребрами. При этом сами «ящики» — трехмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвертой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.
Подобно тому, как трехмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвертое измерение, сформирует гиперкуб. Разрезав шесть граней трехмерного куба, можно разложить его в плоскую фигуру — развертку. Она будет иметь по квадрату с каждой стороны исходной грани плюс еще один — грань, ей противоположную. А трехмерная развертка четырехмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс еще одного — конечной «гиперграни».
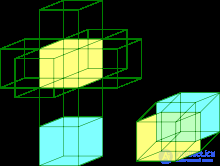
3.3.Стереографическая проекция тора Клиффорда: множество точек (cos(a), sin(a), cos(b), sin(b)), который является подмножеством 3-сферы.



3.4. гиперсфера — гиперповерхность в n-мерном евклидовом пространстве, образованная точками, равноудаленными от заданной точки, называемой центром сферы.
при n = 1 гиперсфера вырождается в две точки, равноудаленные от центра;
при n = 2 она представляет собой окружность;
при n=3 гиперсфера является сферой.
при n=4 гиперсфера является 3-сферой.
Расстояние от центра гиперсферы до ее поверхности называется радиусом гиперсферы. Гиперсфера является (n-1)-мерным подмногообразием в n-мерном пространстве, все нормали к которому пересекаются в ее центре.

3.5. гиперконус
В настоящий момент о нем мало что известно. Так выглядят попытки его изобразить.
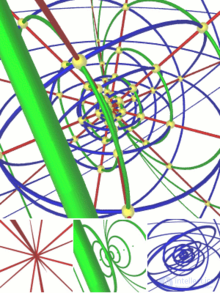
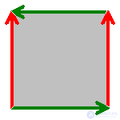
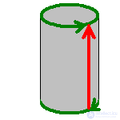
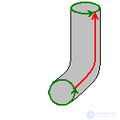
3.6. бутылка клейна - односторонняя поверхность, впервые описанная в 1882 году немецким математиком Ф. Клейном. Она тесно связана с лентой Мебиуса и проективной плоскостью. Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз и, продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырехмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трехмерном евклидовом пространстве.
В отличие от обыкновенного стакана, у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара, можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
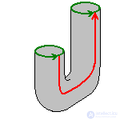
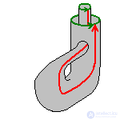
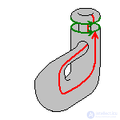
Бутылка Клейна не может быть вложена (только погружена) в трехмерное евклидово пространство, но вкладывается в 4Д.

Бутылка Клейна, погруженная в трехмерное пространство
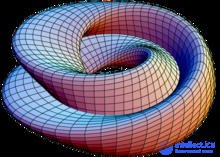
Реализация бутылки Клейна в виде восьмерки.
3-сфера является другой широко обсуждаемой фигурой, располагающейся в четырехмерном пространстве. Но она не является четырехмерным многогранником, поскольку не ограничена многогранными ячейками.
Трехмерная сфе́ра, или трехмерная гиперсфе́ра, иногда 3-сфе́ра, — сфера в четырехмерном пространстве. Состоит из множества точек, равноудаленных от фиксированной центральной точки в четырехмерном евклидовом пространстве. Так же, как двумерная сфера, которая образует границу шара в трех измерениях, 3-сфера имеет три измерения и является границей четырехмерного шара.

Стереографическая проекция параллелей гиперсферы (красная), меридианов (синий) и гипермеридианов (зеленый). В связи с конформными свойствами стереографической проекции, кривые пересекаются друг с другом ортогонально (в желтых точках), как в 4D. Все кривые являются окружностями: кривые, которые пересекаются <0,0,0,1> имеют бесконечный радиус (то есть являются прямыми).
Дуоцилиндр является фигурой в четырехмерном пространстве, связанной с дуопризма ми, хотя это тоже не многогранник.
Дуоцилиндр или двойной цилиндр , представляет собой геометрический объект , встроенный в 4- мерного евклидова пространства , определяется как декартово произведение двух дисков соответствующих радиусов г 1 и г 2 :
Это аналог цилиндра в 3-м пространстве, который представляет собой декартово произведение диска на отрезок прямой . Но в отличие от цилиндра обе гиперповерхности ( обычного дуоцилиндра) конгруэнтны .
Его двойник - это дуошпиндель, состоящий из двух окружностей, одна в плоскости XY, а другая в плоскости ZW.


Стереографическая проекция гребня дуоцилиндра (см. Ниже) в виде плоского тора . Гребень вращается в плоскости XW.
Дуопризма — многогранник, полученный прямым произведением двух многогранников, каждое размерности два и выше. Прямое произведение n-многогранника и m-многогранника — это (n+m)-многогранник, где n и m не меньше 2 (многоугольник или многогранник).
Дуопризмы наименьшей размерности существуют в 4-мерном пространстве как 4-мерные многогранники, будучи прямым произведением двух многоугольников в 2-мерном евклидовом пространстве. Точнее, это множество точек:
,
где P1 и P2 — два множества точек, расположенные в многоугольниках (сомножителях). Если оба многоугольника выпуклы, такая дуопризма выпукла и ограничена призматическими ячейками.
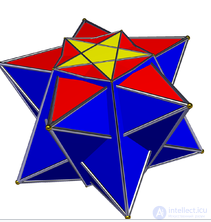
Стереографическая проекция большой дуоантипризмы[en], центрированной относительно пентаграммной скрещенной антипризмы[en]
Правильные 4-мерные многогранники с символом Шлефли имеют ячейки вида
, грани вида
, реберные фигуры
и вершинные фигуры
.
Существование правильных четырехмерных многогранников ограничено существованием правильного многогранника
. Для 4-мерных многогранников предлагается использовать название "полихор"
Каждый вид может существовать в пространстве, зависящем от следующего выражения:
: Гиперсферические 3-мерные соты или 4-мерные многогранники
: Евклидовы 3-мерные соты
: Гиперболические 3-мерные соты
Эти ограничения допустимы для 21 форм — 6 форм выпуклы, 10 не выпуклы, одна является евклидовыми 3-мерными сотами и 4 являются гиперболическими сотами.
Эйлерова характеристика четырехмерного многогранника вычисляется по формуле
и равна нулю для всех видов.
6 выпуклых правильных четырехмерных многогранников показаны в таблице ниже. Все эти многогранники имеют эйлерову характеристику (χ) 0.
| Название | Шлефли {p,q,r} |
Коксетер       |
Ячейки[en] {p,q} |
Граней {p} |
Ребер {r} |
Вершин {q,r} |
Двойственный {r,q,p} |
|---|---|---|---|---|---|---|---|
| Пятиячейник (4-симплекс) |
{3,3,3} |        |
5 {3,3} |
10 {3} |
10 {3} |
5 {3,3} |
(самодвойственен) |
| Тессеракт (4-куб) |
{4,3,3} |        |
8 {4,3} |
24 {4} |
32 {3} |
16 {3,3} |
Шестнадцатиячейник |
| Шестнадцатиячейник (4-ортоплекс) |
{3,3,4} |        |
16 {3,3} |
32 {3} |
24 {4} |
8 {3,4} |
Тессеракт |
| Двадцатичетырехъячейник | {3,4,3} |        |
24 {3,4} |
96 {3} |
96 {3} |
24 {4,3} |
(самодвойственен) |
| Стодвадцатиячейник | {5,3,3} |        |
120 {5,3} |
720 {5} |
1200 {3} |
600 {3,3} |
Шестисотъячейник |
| Шестисотъячейник | {3,3,5} |        |
600 {3,3} |
1200 {3} |
720 {5} |
120 {3,5} |
Стодвадцатиячейник |
| Пятиячейник | Тессеракт | Шестнадцати- ячейник |
Двадцати- четырехъячейник |
Стодвадцати- ячейник |
Шестисотъячейник |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Каркас (Многоугольник Петри) в косой ортогональной проекции | |||||
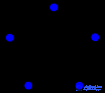 |
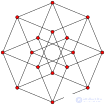 |
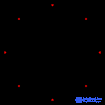 |
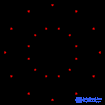 |
 |
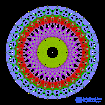 |
| Ортогональная проекция | |||||
 Тетраэдральная оболочка (центрировано по ячейке/вершине) |
 Кубическая оболочка (центрировано по ячейке) |
 Кубическая оболочка (центрировано по ячейке) |
 Кубооктаэдральная оболочка (центрировано по ячейке) |
 Усеченная ромботриаконта- эдральная оболочка[en] (центрировано по ячейке) |
 Пентакиикоси- додекаэдральная оболочка[en] (центрировано по вершине) |
| Диаграммы Шлегеля (перспективная проекция) | |||||
 (центрировано по ячейке) |
 (центрировано по ячейке) |
 (центрировано по ячейке) |
 (центрировано по ячейке) |
 (центрировано по ячейке) |
 (центрировано по вершине) |
| Каркас стереографической проекции (гиперсферический) | |||||
 |
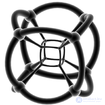 |
 |
 |
 |
 |
4-мерные диэдры и осоэдры существуют как правильные замощения 3-сферы.
Правильные 4-мерные диэдры (2 фасеты = 3-мерные грани) включают: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2} и их двойственные 4-мерные осоэдры (2 вершины): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2,p}. Об этом говорит сайт https://intellect.icu . Многогранники вида {2,p,2} являются одновременно 4-мерными диэдрами и осоэдрами. Существуют также формы {p,2,q}, которые имеют диэдральные ячейки и осоэдральные вершинные фигуры.
| Шлефли {2,p,q} |
Коксетер       |
Ячейки[en] {2,p}π/q |
Граней {2}π/p,π/q |
Ребер | Вершин | Вершинная фигура {p,q} |
Симметрия | Двойственный |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} |        |
4 {2,3}π/3  |
6 {2}π/3,π/3 |
4 | 2 | {3,3} |
[2,3,3] | {3,3,2} |
| {2,4,3} |        |
6 {2,4}π/3  |
12 {2}π/4,π/3 |
8 | 2 | {4,3} |
[2,4,3] | {3,4,2} |
| {2,3,4} |        |
8 {2,3}π/4  |
12 {2}π/3,π/4 |
6 | 2 | {3,4} |
[2,4,3] | {4,3,2} |
| {2,5,3} |        |
12 {2,5}π/3  |
30 {2}π/5,π/3 |
20 | 2 | {5,3} |
[2,5,3] | {3,5,2} |
| {2,3,5} |        |
20 {2,3}π/5  |
30 {2}π/3,π/5 |
12 | 2 | {3,5} |
[2,5,3] | {5,3,2} |
Существует десять правильных 4-мерных звездчатых многогранника, которые называются многогранниками Шлефли—Гесса[en]. Их вершины располагаются на выпуклом стодвадцатиячейнике {5,3,3} и шестисотъячейнике {3,3,5}.
Людвиг Шлефли нашел четыре из них и отбросил остальные шесть, поскольку не позволял нарушение эйлеровой характеристики на ячейках или вершинных фигурах (F+V−E=2). Эдмунд Гесс (Edmund Hess, 1843–1903) завершил список в своей книге Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder ( , 1883) (Введение в учение о замощении сферы с учетом теории равногранных и равноугольных многогранников) .
Существует 4 расположения ребер[en] и 7 расположений граней[en] в этих 10 правильных звездчатых 4-мерных многогранниках, показанные как ортогональные проекции:
| Название | Каркас | Тело | Шлефли {p, q, r} Коксетер |
Ячеек {p, q} |
Граней {p} |
Ребер {r} |
Вершин {q, r} |
Плот- ность[en] |
χ | Группа симметрии | Двойственный {r, q,p} |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Икосаэдральный 120-ячейник[en] (ограненный Шестисотячейник) |
 |
 |
{3,5,5/2}         |
120 {3,5}  |
1200 {3}  |
720 {5/2}  |
120 {5,5/2}  |
4 | 480 | H4 [5,3,3] |
Малый звездчатый 120-ячейник |
| Малый звездчатый 120-ячейник[en] |  |
 |
{5/2,5,3}         |
120 {5/2,5}  |
720 {5/2}  |
1200 {3}  |
120 {5,3}  |
4 | −480 | H4 [5,3,3] |
Икосаэдральный 120-ячейник |
| Большой 120-ячейник[en] |  |
 |
{5,5/2,5}         |
120 {5,5/2}  |
720 {5}  |
720 {5}  |
120 {5/2,5}  |
6 | 0 | H4 [5,3,3] |
Самодвойственный |
| Великий 120-ячейник[en] |  |
 |
{5,3,5/2}         |
120 {5,3}  |
720 {5}  |
720 {5/2}  |
120 {3,5/2}  |
20 | 0 | H4 [5,3,3] |
Большой звездчатый 120-ячейник |
| Большой звездчатый 120-ячейник[en] |  |
 |
{5/2,3,5}         |
120 {5/2,3}  |
720 {5/2}  |
720 {5}  |
120 {3,5}  |
20 | 0 | H4 [5,3,3] |
Великий 120-ячейник |
| Великий звездчатый 120-ячейник[en] |  |
 |
{5/2,5,5/2}           |
120 {5/2,5}  |
720 {5/2}  |
720 {5/2}  |
120 {5,5/2}  |
66 | 0 | H4 [5,3,3] |
Самодвойственный |
| Большой великий 120-ячейник[en] |  |
 |
{5,5/2,3}         |
120 {5,5/2}  |
720 {5}  |
1200 {3}  |
120 {5/2,3}  |
76 | −480 | H4 [5,3,3] |
Большой икосаэдральный 120-ячейник |
| Большой икосаэдральный 120-ячейник[en] (большой ограненый 600-ячейник) |
 |
 |
{3,5/2,5}         |
120 {3,5/2}  |
1200 {3}  |
720 {5}  |
120 {5/2,5}  |
76 | 480 | H4 [5,3,3] |
Великий большой 120-ячейник |
| Великий 600-ячейник[en] |  |
 |
{3,3,5/2}         |
600 {3,3}  |
1200 {3}  |
720 {5/2}  |
120 {3,5/2}  |
191 | 0 | H4 [5,3,3] |
Великий большой звездчатый 120-ячейник |
| Большой великий 120-ячейник[en] |  |
 |
{5/2,3,3}         |
120 {5/2,3}  |
720 {5/2}  |
1200 {3}  |
600 {3,3}  |
191 | 0 | H4 [5,3,3] |
Великий 600-ячейник |
Существует 4 несостоявшихся правильных звездчатых перестановок многогранников: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Их ячейки и вершинные фигуры существует, но они не покрывают гиперсферу конечным числом представлений.
Не существует невыпуклых правильных многогранников в размерностях 5 и выше.
В 4-мерном пространстве 5 из 6 выпуклых правильных многогранников образуют проективные 4-мерные многогранники. 3 специальных случая — это полудвадцатичетырехъячейник, полушестисотъячейник и полустодвадцатиячейник.
| полутессеракт | {4,3,3}/2 | {4,3,3}4 | 4 | 12 | 16 | 8 | 0 |
|---|---|---|---|---|---|---|---|
| полушестнадцатиячейник | {3,3,4}/2 | {3,3,4}4 | 8 | 16 | 12 | 4 | 0 |
| полудвадцатичетырехъячейник | {3,4,3}/2 | {3,4,3}6 | 12 | 48 | 48 | 12 | 0 |
| полустодвадцатиячейник | {5,3,3}/2 | {5,3,3}15 | 60 | 360 | 600 | 300 | 0 |
| полушестисотъячейник | {3,3,5}/2 | {3,3,5}15 | 300 | 600 | 360 | 60 | 0 |
4.1. 4D геометрические тела в литературе.
Тессеракт настолько интересная фигура, что неоднократно привлекал внимание писателей и кинематографистов. Математические абстракции вызвали к жизни представление о существовании параллельных миров. Под таковыми понимаются реальности, которые существуют одновременно с нашей, но независимо от нее. В параллельном мире события происходят по-своему, он может отличаться от нашего мира, как в отдельных деталях, так и практически во всем. При этом физические законы параллельного мира не обязательно аналогичны законам нашей Вселенной.
Герберт Уэллс, одним из первых описавший путешествие во времени, во многих других своих произведениях затронул также и невидимые измерения пространства: «Чудесное посещение», «Замечательный случай с глазами Дэвидсона», «Хрустальное яйцо», «Украденное тело», «Люди как боги», «История Платтнера». В последнем рассказе человек, выброшенный катастрофой из нашего мира и затем вернувшийся, претерпевает пространственное отражение — например, сердце у него оказывается с правой стороны. Владимир Набоков описал аналогичное изменение пространственной ориентации в романе «Смотри на арлекинов!» (1974). В научной фантастике второй половины XX века четвертое измерение использовали такие крупные писатели, как Айзек Азимов, Артур Кларк, Фредерик Пол, Клиффорд Саймак и многие другие. Создание четырехмерного тессеракта лежит в основе сюжета рассказа Роберта Хайнлайна, названного в русском переводе «Дом, который построил Тил».Валерий Брюсов в 1924 году написал стихотворение «Мир N измерений».
В мистической литературе четвертое измерение нередко описывается как обиталище демонов или душ умерших. Эти мотивы встречаются, например, у Джорджа Макдональда (роман «Лилит»), в нескольких рассказах Амброза Бирса, в рассказе А. П. Чехова «Тайна». В романе Дж. Конрада и Ф. М. Форда «Наследники» (1901) обитатели четвертого измерения пытаются захватить нашу Вселенную.
4.2. 4D геометрические тела в изобразительном искусстве
Концепция четвертого измерения оказала значительное влияние на изобразительное искусство. Роль перспективы снизилась; например, кубисты (Пикассо, Метценже и другие) в своих картинах часто изображали людей и предметы одновременно в различных ракурсах, тем самым как бы добавляя им измерения.

Пабло Пикассо «Авиньонские девицы». 1907г
«Распятие на кресте» — картина испанского художника Сальвадора Дали, написанная в 1954 году, изображает распятого Иисуса Христа на развертке тессеракта. Картина хранится в Музее Метрополитен в Нью-Йорке


С.Дали « В поисках четвертого измерения»
Гийом Аполлинер в 1913 году писал.: Сегодня ученые больше не ограничивают себя тремя измерениями Евклида. И художники, что совершенно естественно, привлекли новые возможности пространственных измерений, что на языке современных студий стало называться четвертым измерением. Существуя в сознании образом пластики предмета, четвертое измерение зарождается благодаря трем известным измерениям: оно представляет собой необъятность пространства во всех направлениях в каждый данный момент. Это само пространство, само измерение бесконечности; четвертое измерение одаряет предметы пластичностью.
Поиском новых средств занимался сюрреалист Марсель Дюшан, хорошо знакомый с многомерной математикой и методами ее визуализации. Среди наиболее характерных образцом его творчества — картина «Большое стекло». Аналогичные мотивы прослеживаются у футуристов, супрематистов («работы Малевича этого периода напоминают плоские сечения объектов из высших измерений») и сюрреалистов.

М. Дюшан. «Большое стекло: новобрачная, обнажаемая своими холостяками», 1915–1923 годы, Филадельфия.
4.3. 4D геометрические тела в архитектуре (слайды)
Вывод: Чтобы увидеть плоскость надо выпрыгнуть из нее. Чтобы увидеть объемное трехмерное тело, надо его повернуть, ведь мы видим только плоскую картинку – проекцию трехмерного тела на двумерную плоскость. А чтобы представить 4D тело, надо спроецировать его на трехмерное пространство, как бы поместить тело вовнутрь себя. Нашему воображению это сделать очень трудно, наш глаз не может видеть предмет со всех сторон. Но попытки заглянуть в четвертое измерение, найти там объекты доступные для восприятия не покидают математиков.
Есть древняя неразрешимая задача. Надо соединить три дома с тремя колодцами, но так, чтобы жители каждого из домов могли ходить по воду в любой колодец и при этом пути их не должны пересекаться. Задача неразрешима на плоскости, а на торе, то есть бублике, например, все получается просто.
Исследование, описанное в статье про фигуры четырехмерного пространства, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое фигуры четырехмерного пространства, дуопризма, дуоцилиндр, гиперсфера, бутылка клейна, гиперконус, тор клиффорда, гиперкуб, многогранник дюрера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Стереометрия
Комментарии
Оставить комментарий
Стереометрия
Термины: Стереометрия