Лекция
Привет, Вы узнаете о том , что такое блоки, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое блоки, алгоритмы устройства управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
В состав устройства управления системы, предназначенной для решения локальных задач, рассмотренных в п.1.4, входят задающий блок (ЗБ) и регулятор выходных переменных (рис. 1.23).
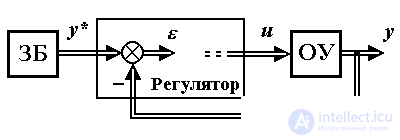
Рис. 1.23. Многоканальная система управления
Замечание 1.8. В современных системах блоку не обязательно соответствует физическое устройство, в большинстве случаев -это алгоритм или программа расчетов требуемых переменных (сигналов), что соответствует кибернетической трактовке понятия блока (см. п. 1.1).
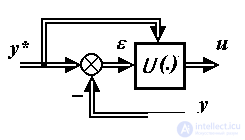 Алгоритмом управления называется набор аналитических выражений, используемых для расчета управляющих воздействий (термин "алгоритм" происходит от имени Ал-Хорезми и подразумевает систему операций, выполняемых по определенным правилам).
Алгоритмом управления называется набор аналитических выражений, используемых для расчета управляющих воздействий (термин "алгоритм" происходит от имени Ал-Хорезми и подразумевает систему операций, выполняемых по определенным правилам). Типовой алгоритм управления по выходной переменной y имеет вид:
(1.11) u= U ( 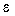 , y*,...),
, y*,...),
где рассогласование 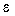 рассчитывается по формуле:
рассчитывается по формуле:
(1.12) 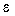 = y*- y,
= y*- y,
а в качестве оператора U (·) могут выступать как алгебраические и трансцендентные функции, так и интегро-дифференциальные операторы, операторы Лапласа, Булевы функции и т.д.
Простейшими алгоритмами управления (регуляторами) являются регуляторы отклонения вида:
(1.13) u = U ( 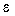 ).
).
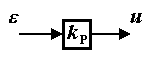
К ним относятся: пропорциональный, или П-регулятор, для которого
(1.14) u = kP e,
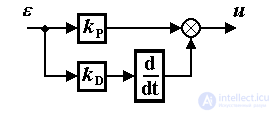
где kP - постоянный коэффициент ; пропорционально-дифференциальный, или ПД-регулятор :
(1.15) 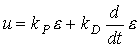 ,
,
где kD - постоянный коэффициент ;
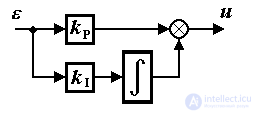
пропорционально-интегральный, или ПИ-регулятор :
(1.16) 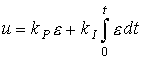 ,
,
где kI - постоянный коэффициент, а также пропорционально-интегрально-дифференциальный (ПИД-регулятор )
(1.17) 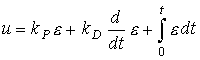 .
.
1.5.2. Задающие блоки . Задающим блоком называется блок (алгоритм), осуществляющий расчет задающего воздействия y*(t ). Об этом говорит сайт https://intellect.icu . В простейших случаях в качестве таких блоков выступают задающие рукоятки и пульты, а в более совершенных системах - аппаратно и программно реализованные генераторы задающих сигналов.
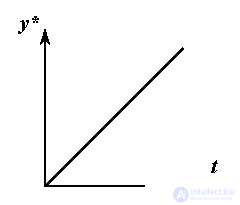
К простейшим задающим блокам можно отнести блоки, генерирующие сигналы для задач стабилизации, где y* = Y* = const, и элементарных задач слежения. Так для организации движения объекта управления с постоянной скоростью 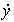 = V* =const используется алгоритм, описываемый дифференциальным уравнением
= V* =const используется алгоритм, описываемый дифференциальным уравнением
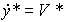 , y*(0)=Y*,
, y*(0)=Y*,
обеспечивающий генерацию сигнала y*(t)=Y*+V*t. Для движения с постоянным ускорением 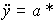 = const применяется алгоритм
= const применяется алгоритм
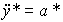 , y*(0)=Y*,
, y*(0)=Y*, 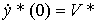 ,
,
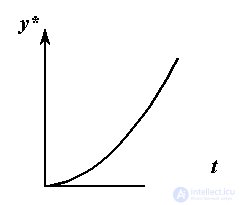
обеспечивающий генерацию сигнал y*=Y*+V*t+a*t2/2 и т.д.
Более сложным задающим блоком является интерполятор - многоканальный задающий блок, предназначенный для расчета текущих значений согласованных задающих воздействий ( см. п.1.4 ) , т.е. сигналов yj*(t) , подчиненных функциональной зависимости:
(1.18) 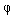 (y1*,y2*,...,ym*) = 0.
(y1*,y2*,...,ym*) = 0.
Выходные сигналы интерполятора используются в следящих системах, обеспечивающих решение задач согласованного управления и, в частности, траекторного управления многозвенными механическими системами, где требуемая траектория движения рабочей точки S механизма задана уравнением ( 1.8).
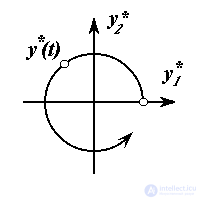
Пример 1.7. Интерполятор системы управления роботом-манипулятором, схват которого перемещается по окружности (1. 10 ), генерирует двумерное задающее воздействие
y*(t)={y1*(t),y2*(t)}
и описывается системой дифференциальных уравнений
(1.19) 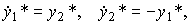
с начальными значениями y*10=R, y*20=0. Система имеет решение
(1.20) y*1 =R cos t, y*2 = R sin t,
которое удовлетворяют уравнению (1.10).
Многие современные САУ строятся как системы управления состоянием объекта, т.е. обеспечивают решения задач стабилизации состояния
x = x*=const
или слежения по состоянию, т.е. соблюдение заданного закона изменения вектора состояний:
x = x*(t),
где x*={x*i} - вектор задающих воздействий по состоянию. Алгоритмы управления таких систем имеют вид
(1.21) u=U(e, x*,...),
где рассогласование e рассчитывается по формуле:
(1.22) e = x*- x.
Структура системы управления состоянием иллюстрируется рис. 1.24.
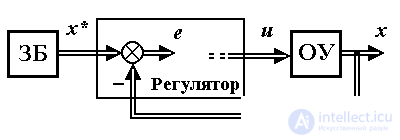
Рис. 1.24. Система управления состоянием
1.5.3. Специальные блоки систем управления и контроля. Для решения задач автоматического контроля, возникающих как в САУ, так и в системах контроля, используются наблюдатели и идентификаторы.
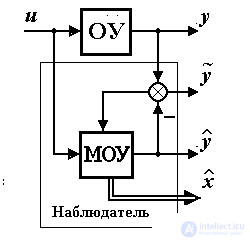
Наблюдателем называется блок (алгоритм), предназначенный для оценивания неизмеряемых переменных состояния ОУ xiили внешней среды. Структура наблюдателя ОУ включает в себя модель объекта управления МОУ, которая вырабатывает текущие значения оценки 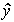 (t ) выходной переменной y(t ) и оценки
(t ) выходной переменной y(t ) и оценки 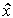 (t) вектора состояния x(t) . Поведение модели корректируется за счет обратных связей по ошибке наблюдения (невязке )
(t) вектора состояния x(t) . Поведение модели корректируется за счет обратных связей по ошибке наблюдения (невязке )
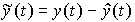 .
.
Наблюдатель применяется в системах управления состоянием (рис. 1.25), в которых не все переменные состояния могут быть измерены или измерения xi содержат значительные помехи . В этих случаях рассмотренный ранее алгоритм управления (1.21) принимает вид
(1.23) u= K (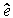 , x*,...),
, x*,...),
где оценка рассогласования 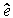 рассчитывается по формуле:
рассчитывается по формуле:
(1.24) 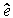 = x* -
= x* - 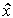 .
.
Математическая модель (уравнение) объекта управления содержит коэффициенты 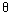 i - массо-инерционные, электрические и термодинамические параметры управляемого процесса и других используемых в САУ устройств. Параметры объединяются в вектор параметров
i - массо-инерционные, электрические и термодинамические параметры управляемого процесса и других используемых в САУ устройств. Параметры объединяются в вектор параметров
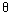 = {
= { 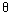 i}
i}
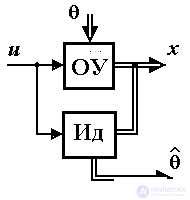
В тех случаях когда значения параметров изменяются во времени или заранее неизвестны, появляется необходимость в использовании идентификаторов параметров. Идентификатором называется блок (алгоритм) вида
(1.25) 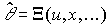 ,
,
где 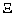 (·) - динамический оператор, предназначенный для оценивания параметров ОУ, т.е. расчета в реальном времени значения текущей оценки
(·) - динамический оператор, предназначенный для оценивания параметров ОУ, т.е. расчета в реальном времени значения текущей оценки 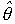 (t ) вектора
(t ) вектора 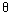 по имеющейся информации о текущем состоянии x(t) и входном воздействии u(t) объекта.
по имеющейся информации о текущем состоянии x(t) и входном воздействии u(t) объекта.
Идентификаторы применяются в адаптивных системах управления, т.е. в системах, в которых параметры регулятора настраиваются в процессе работы системы. В них используются адаптивные алгоритмы управления вида:
(1.26) u= U (e, x*,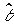 ...),
...),
где вектор оценки 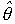 может быть получен с помощью алгоритма идентификации (1.25).
может быть получен с помощью алгоритма идентификации (1.25).
Прочтение данной статьи про блоки позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое блоки, алгоритмы устройства управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про блоки
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления