Лекция
Привет, Вы узнаете о том , что такое магнитный поток, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое магнитный поток , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Магни́тный пото́к — поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля |B| на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по ее малым фрагментам. Стандартное обозначение — Φ.
Другими словами, закон Гаусса для магнетизма — это утверждение:
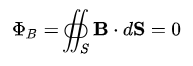
для любой замкнутой поверхности S.
Важнейшая физическая формула, в которую входит магнитный поток , — выражение для закона электромагнитной индукции Фарадея.
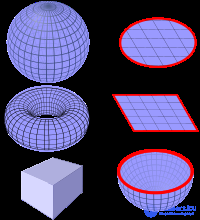
Некоторые примеры замкнутых поверхностей (слева) и открытых поверхностей (справа). Слева: Поверхность сферы, поверхность тора , поверхность куба. Справа: Поверхность диска , квадратная поверхность, поверхность полусферы. (Поверхность синяя, граница красная.)
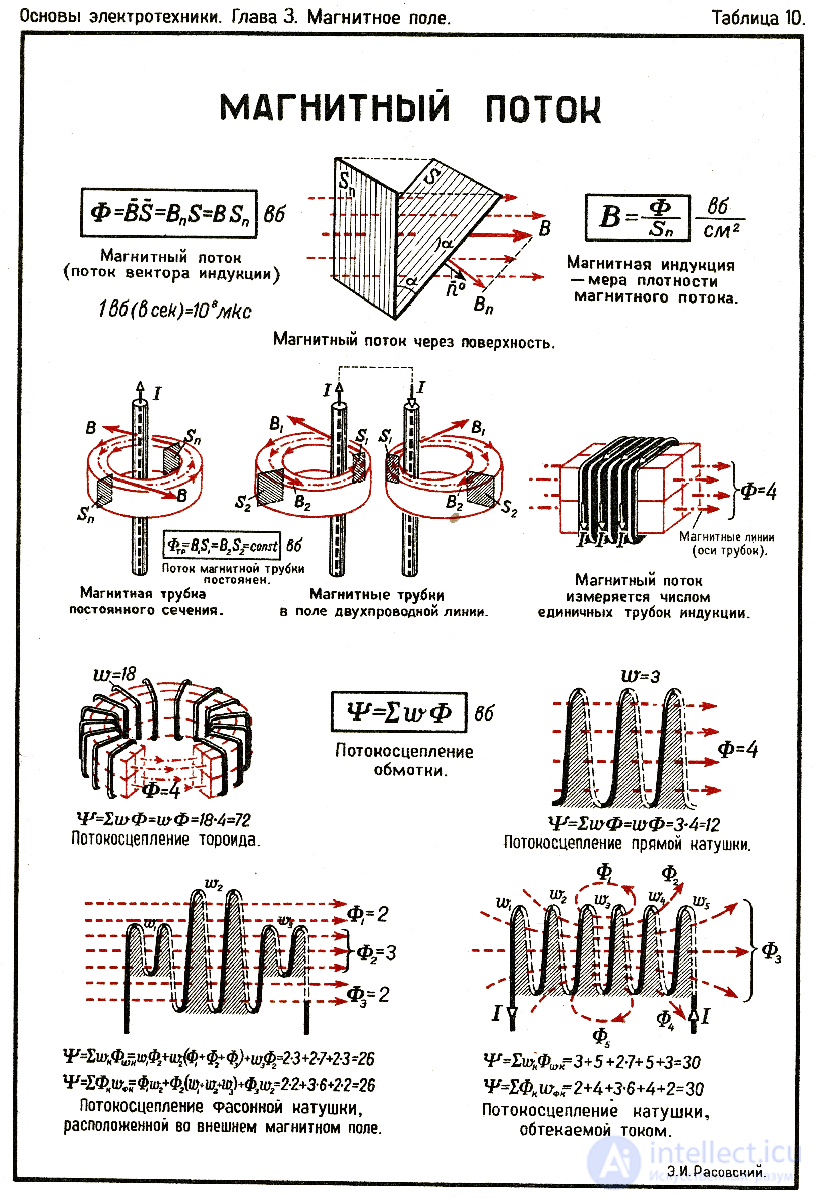
Разбиение поверхности на малые участки dS
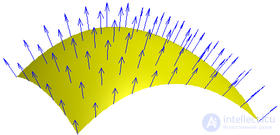
Изменение вектора нормали к поверхности
Магнитным потоком через бесконечно малый элемент поверхности dS называется произведение
,
где α — угол между вектором магнитной индукции B и единичным вектором нормали n к участку поверхности, а векторный элемент dS площади поверхности S определяется как
.
Магнитным потоком через поверхность конечной площади называется интеграл от dΦ по поверхности:
.
Направление вектора n
в общем случае непостоянно (см. Об этом говорит сайт https://intellect.icu . рис.), магнитное поле также может изменяться вдоль поверхности. Точка в произведениях означает скалярное умножение векторов. Интеграл понимается как предел суммы по малым участкам при стремлении их размеров к нулю. Поверхность может быть незамкнутой (как на рис.) или замкнутой.
В случае однородного поля и плоской поверхности магнитный поток рассчитывается как Φ=BScosα
.
В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с = кг·м²·с-2·А-1), в системе СГС — максвелл (Мкс, 1 Вб = 108 Мкс).
Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.
В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции B через любую замкнутую поверхность S равен нулю:
.
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
В соответствии с теоремой Стокса, магнитный поток Φ через поверхность, «натянутую» на некий контур L, можно выразить через циркуляцию векторного потенциала A магнитного поля по этому контуру:
,
поскольку имеет место связь B=rotA
. Этот поток не зависит от конфигурации натянутой поверхности.
По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создается электродвижущая сила
E=−dΦdt
в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нем возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции B
и/или геометрии контура.
При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:
,
где h — постоянная Планка, e — элементарный заряд.
Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):
Вб (в СИ);
Гаусс·см2 (в СГС), c — скорость света.
Экспериментально квантование магнитного потока было обнаружено в 1961 году.
Исследование, описанное в статье про магнитный поток, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое магнитный поток и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Из статьи мы узнали кратко, но содержательно про магнитный поток
Комментарии