9 Проводящий и диэлектрический шар в однородном электростатическом поле кратко

Привет, Вы узнаете о том , что такое шар в однородном электростатическом поле, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое шар в однородном электростатическом поле , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

1. Постановка задачи

В однородное электрическое поле Еo вносится идеально проводящий шар или шар из идеального диэлектрика. Требуется найти возмущенное поле. Ясно, что на больших расстояниях от шара поле будет невозмущенным и равно Еo (рис. 1). Очевидно, что для нахождения возмущенного поля целесообразно использовать .сферкческую систему координат

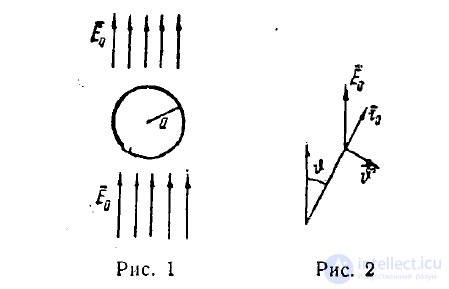
Рис. 1 Рис. 2

Однородное поле в этой системе координат представится формулами (рис. 2).

Потенциал 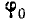однородного поля в этой же системе координат, к с. к нетрудно проверить по формуле 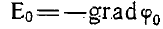равен

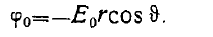(1)

Нахождение возмущенного поля, как в общем случае, имеет место в теории электромагнитного поля, проводится двумя этапами:
а) находится решение, удовлетворяющее уравнениям Максвелла;
б) подбираются неизвестные постоянные, входящие в решение таким образом, чтобы были удовлетворены граничные условия на границе сред.
Однако зачастую оказывается возможным воспользоваться готовым решением и таким образом свести решение задачи только к выполнению второго этапа. Ниже поставленную задачу мы будем
решать именно этим путем.

2. Идеально проводящий шар в однородном электростатическом поле

Хорошо известен метод решения следующей простой задачи:
имеется точечный заряд над идеально проводящей плоскостью, требуется найти поле над этой плоскостью. Эта задача решается методом зеркальных изображений. Этот метод состоит в том,
что поле над плоскостью представляется в виде суммы полей реального заряда и его зеркального изображения, имеющего протиьоположный знак. Как видим, суть этого метода в том, что используется
готовое решение уравнений Максвелла — таким является поле воображаемого заряда, причем положение этого заряда подобрано так, что суммарное поле удовлетворяет граничному условию
на идеально проводящей плоскости .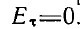

Метод зеркальных изображений наводит на мысль о возможности подбора такой воображаемой системы, зарядов внутри шара,
чтобы поле этих зарядов совместно с однородным полем Е0 удовлетворяло
граничному условию на поверхности шара
. Об этом говорит сайт https://intellect.icu . (2)
Вытекающее из этого условия граничное условие для потенциала 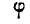таково:

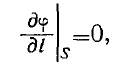
где l — любая кривая на поверхности шара S. Отсюда следует, что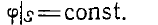
Итак,

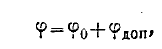
где 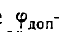— потенциал искомой системы зарядов внутри шара.

Из формулы (1) следует, что <рдоп должно содержать множитель 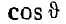(граничное условие должно выполняться при любом ô), а такой
множитель содержится в выражении для потенциала диполя.

Поэтому положим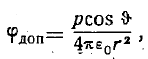

где р —• искомый момент диполя. Следовательно,

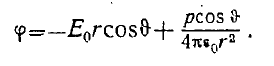
На поверхности шара, т. е. при г —а, должно выполняться условие

Так как это равенство должно выполняться при любом , то
оно возможно только тогда, когда

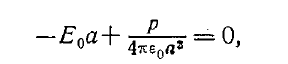
откуда получаем

(3)
и задача решена. На рис. 3 показаны векторные линии поля Е.

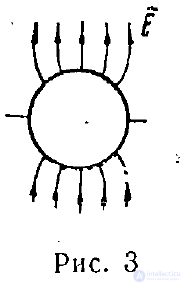
рис. 3

3. Диэлектрический шар в однородном N электростатическом поле

В этом случае, в отличие от предыдущего, должны выполняться два граничных условия:
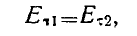(4)
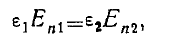(5)
где ,— диэлектрические проницаемости внутри и вне шара (рис. 4).
Граничному условию (4) соответствует условие для потенциала

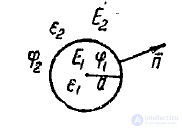
Рис. 4

Это граничное условие сводится к следующему:

поскольку в бесконечности потенциал 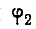должен равняться нулю.
Таким образом, на поверхности- шара должно выполняться условие
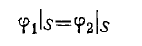(6)

и условие, соответствующее (5),
(7)

В случае идеально проводящего шара поле внутри его равно нулю. В случае же диэлектрика поле внутри шара отлично от нуля.
Поэтому должны быть две неизвестные величины соответственно двум граничным условиям. Если попытаться решить задачу путем подбора поля диполя, то это даст одно неизвестное—< момент диполя
р. Очевидно, что вторым неизвестным должно быть поле Е, внутри шара. Итак, полагая поле Eh параллельным полю Е0 внутри шара однородным, имеем

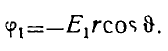
Вне шара

Подставляем эти выражения в граничные условия (6) и (7), и получаем систему уравнений

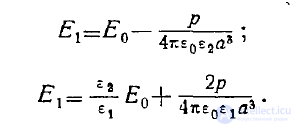
Решая ее, находим

(8)

В частности, при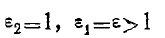
(9)

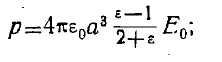
(10)

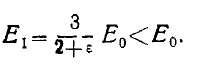
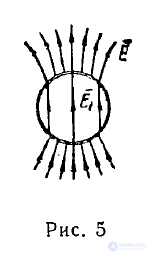
Рис. 5
Конфигурация векторных линий поля Е для этого случая изображена на рис. 5. В связи с неравенством (10) вводят понятие фактора деполяризации, который определяется по формуле

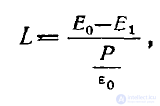
где Р — вектор поляризации внутри "диэлектрика шара.
Учитывая, что 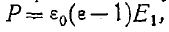находим

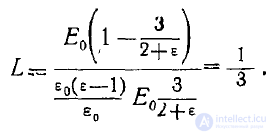
Рассмотренное решение задачи о шаре используется при изучении рассеяния электромагнитных волн в атмосфере и в других средах.

Исследование, описанное в статье про шар в однородном электростатическом поле, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое шар в однородном электростатическом поле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля

Из статьи мы узнали кратко, но содержательно про шар в однородном электростатическом поле