Лекция
Привет, Вы узнаете о том , что такое внутренняя и внешняя задачи электродинамики, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое внутренняя и внешняя задачи электродинамики, теорема о единственности решения внутренней задачи электродинамики, формулы грина , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Методы решения уравнений Максвелла и свойства полученных решений существенно зависят от формы области пространства, в которой определяется ЭМП, электрофизических свойств заполняющей его среды, распределения источников возбуждения и заданных граничных условий. При этом задачи отыскания электромагнитных полей, можно разделить на две группы: внутренние и внешние задачи электродинамики.
Внутренней называется задача нахождения электромагнитного поля в конечном объеме V , который со всех сторон ограничен замкнутой поверхностью S . Другими словами, в результате решения внутренней задачи мы находим электромагнитное поле внутри некоторого замкнутого объема V.
Внешняя задача электродинамики состоит в нахождении полей в неограниченном пространстве, за исключением некоторых областей, в которых это
поле может быть отсутствует. В этом случае мы находим поля вне некоторого объема V, поэтому и задача именуется внешней.
Рассмотрим условия существования и единственности обеих этих задач электродинамики.
Рассмотрим область пространства V, заполненную
линейной средой с известными параметрами, в которой имеются источники электромагнитного поля ст j
r
.
Известно, что поле внутри выделенной области можно описать системой уравнений Максвелла. Докажем, что решение этой системы при заданных граничных условиях и известном распределении источников поля будет единственным. Для этого сформулируем условия единственности решения внутренних задач электродинамики в виде следующей теоремы.
Внутренняя задача электродинамики будет иметь единственное решение,
если на поверхности S , ограничивающей рассматриваемую область пространства, задано какое-либо из следующих граничных условий:
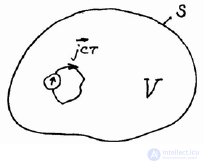
Рисунок 5.1
Доказательство теоремы будем проводить от противного, т.е. предположим, что в результате решения поставленной задачи могут быть получены
два различных решения: одно из которых поле, описываемое векторами 1 E&r
, а второе – векторами 
. Оба эти решения должны удовлетворять уравнениям Максвелла, поэтому мы можем записать:
Вычитая из первой пары уравнений вторую пару уравнений, имеем:
Разность полей 
представляет собой третье поле 
. Если мы докажем, что это поле тождественно равно нулю, то это будет означать, что разницы между предполагаемыми решениями нет, т.е. система уравнений Максвелла имеет единственное решение.
является линейной комбинацией решений, которая должна удовлетворять следующей системе уравнений:
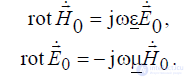
Применяя теорему Умова-Пойнтинга для поля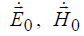 
в рассматриваемом объеме V и оставляя в ней равенство только вещественных слагаемых, можно получить следующее соотношение:
, (5.3)
где учтено, что 
Преобразуем подынтегральное выражение в левой части последнего равенства, используя свойство смешанного произведения трех векторов:
Отсюда следует, что подынтегральное выражение в левой части равенства (5.3) пропорционально тангенциальным компонентам электрического или магнитного полей
– τ 0 E& r
или τ 0 H&
на S. Однако в силу заданных на S граничных условий (5.1), которым должны подчиняться оба решения задачи, имеет место одно из двух равенств:
что в совокупности с равенствами (5.2) приводит к следующим тождествам:
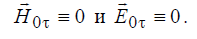
Следовательно, интеграл в левой части рассматриваемого равенства равен нулю:
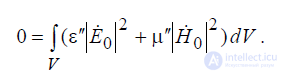. (5.4)
Рассмотрим теперь интеграл в правой части (5.4). Положим, что мнимые
части диэлектрической и магнитной проницаемости среды внутри объема V
не равны нулю ( ε′′ ≠ 0 и μ′′ ≠ 0). Это может быть в двух случаях:
а) когда в среде имеет место поглощение энергии, тогда ε′′ > 0, μ′′ > 0 ;
б) среда является регенеративной (т.е. сама является источником энергии), тогда ε′′ < 0 , μ′′ < 0.
В общем случае, правая часть равенства (5.4) будет равна нулю только тогда, когда
. (5.5)
Последние равенства являются доказательством теоремы о единственности решения внутренних задач электродинамики.
Таким образом, мы доказали, что решение внутренней задачи электродинамики существует и оно единственно, если
а) среда, заполняющая объем V , является поглощающей или регенеративной;
б) на поверхности S задана касательная составляющие электрического τ Er или магнитного τ Hr полей.
Поставим задачу следующим образом. Пусть в рассматриваемой области пространства имеется некоторый ограниченный объем V1, где сосредоточены все источники поля.
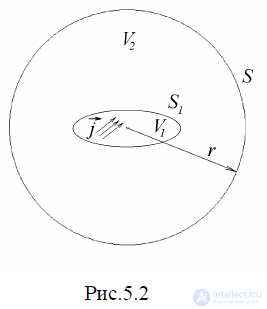
Эти источники создают электромагнитное поле в окружающем его пространстве, том
числе и внешнем по отношению к объему V1.
Это поле может быть найдено путем решения
системы уравнений Максвелла. Найдем ус-ловия, при которых решение этой системы
является единственным для области пространства, внешней по отношению к объему
V1. Окружим этот объем сферой большого радиуса r и будем искать решение
задачи внутри этой сферы в объеме V2 , заключенном между поверхностями
S1 и S2 , где нет источников поля.
В таком случае мы имеем дело с внутренней задачей электродинамики, единственность которой нами доказана выше. Для этого необходимо, чтобы
среда внутри V2 была поглощающей или регенеративной ( ε′′ ≠ 0, μ′′ ≠ 0), а также отсутствовал поток вектора Пойнтинга разностного поля 0 0,H E & r
& r
через
ограничивающую его поверхность. В данном случае последнее условие имеет вид:
. (5.6)
Пусть на S1 заданы граничные условия (5.1), откуда следует:
тогда
.
Для доказательства теоремы нам необходимо найти условия, при которых
второй интеграл в (5.5). Начнем безгранично увеличивать радиус очерченной
нами сферы, т.е. устремим r → ∞. Об этом говорит сайт https://intellect.icu . В сферической системе координат дифференциал dS = r 2 sin θ dθ dϕ, поэтому нетрудно установить, что для того, чтобы
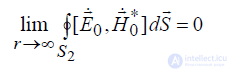
необходимо, чтобы амплитуды напряженности полей 0 0,H E & r
& r
при r → ∞
убывали бы быстрее, чем
r
1 . Тогда
Таким образом, условия единственности решения внешней задачи ЭД
можно сформулировать следующим образом:
Решение внешней задачи ЭД существует и единственно, если
а) среда, заполняющая пространство является поглощающей;
б) на поверхности S1 области V1, вне которой определяется поле, заданы
касательные составляющие Eτ или Hτ ;
в) амплитуды напряженности электрического и магнитного полей E& и
H& при r →∞ убывают быстрее, чем 1 r (условие Зоммерфельда).
5.4. Принцип перестановочной двойственности уравнений Максвелла
Мы уже знаем, что ЭМП в пространстве возбуждается электрическими
зарядами и токами. Распределение этих токов и зарядов в большинстве случаев является достаточно сложным, что заметно затрудняет решение задачи
определения полей. В таких случаях принимают различные приемы, чтобы
как-то облегчить ее решение. Один из таких приемов, позволяющий в ряде
случаев существенно помочь в решении уравнений Максвелла, состоит в
введении фиктивных магнитных токов и зарядов.
Возможность их введения обусловлена тем, что ими мы заменяем вполне
определенные электрические токи и заряды, при условии, что магнитные источники создают в окружающем пространстве такое же ЭМП, как и реальные
электрические источники. Другими словами, чтобы облегчить решение уравнений Максвелла, мы заменяем заданную совокупность токов и зарядов, которые являются реальными источниками поля, другой совокупностью источников поля – фиктивными магнитными зарядами и токами, которые создают
такое же ЭМП, как и реальные источники. Фиктивными магнитные источники считаются потому, что на самом деле в природе их не существует, а введение их есть некий математический прием, облегчающий решение опреде-
ленной задачи. Итак, если в исходной системе уравнений Максвелла (реальные электрические источники поля заменить на эквивалентные им фиктивные магнитные источники поля, (т.е. сделать в них замены: j& r
на м j& r
и ρ& на
ρ&м), то получим новую систему (см. табл.5.1).
При этом dt d j м м div ρ − = & & r
Легко заметить, что систему уравнений (5.8) можно получить из (5.7) и
наоборот, если в них сделать следующие замены:
. (5.10)
Объединение выражений (5.7) и (5.8) дает возможность получить обобщенную систему уравнений Максвелла (5.9), которая содержит и электрические, и магнитные источники поля. Нетрудно показать, что обобщенная система (5.9) при выполнении перестановок (5.10) остается без изменений. Отмеченное свойство получило наименование перестановочной двойственности
уравнений Максвелла.
Как можно воспользоваться данным свойством?
Предположим, что нам известно решение задачи №1 нахождения полей
E& r
и H& r
в заданной области V, создаваемых известным распределением электрических источников поля ρ& и j& r
. Предположим теперь, что появилась необходимость решить другую задачу (№2), которая отличается от предыдущей
только тем, что источниками поля в ней служат магнитные токи и заряды m j& v
и ρ& , распределенные в пространстве точно так, как и электрические в предыдущей задаче. В таком случае в подробном решении задачи №2 нет необходимости, поскольку его можно получить непосредственно из решения задачи
№1, пользуясь свойством перестановочной двойственности уравнений Максвелла. Для этого в уже найденных в результате решения задачи №1 выражениях для полей E& r
и H& r
необходимо сделать перестановки (5.10), и мы получим готовое решение задачи №2. Найденное таким путем решение удовле-
творяет новым граничным условиям на поверхности S, получающимся из прежних путем тех же перестановок. Если, например, в исходной задаче была
равна нулю касательная составляющая поля H
r
на S, то теперь должна обращаться в нуль касательная составляющая поля E
r
.
Таким образом, принцип перестановочной двойственности уравнений
Максвелла позволяет существенно облегчит решение многих важных практических задач электродинамики и, поэтому, нашел широкое применение в
теории ЭМП.
Получим некое вспомогательное математическое соотношение, называемое леммой Лоренца, которое имеет особое значение при постановке и решении краевых задач электродинамики. Для этого рассмотрим безграничную
изотропную среду с параметрами
ε, μ, σ, σм , где компактно расположены
две области пространства V1 и V2 , в каждой из которых имеются свои источники
электромагнитного поля одной частоты.
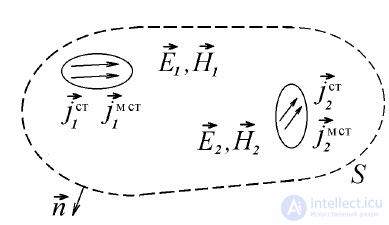
Рисунок 5.3
Пусть эти источники будут заданы распределениями объемных электрических и
магнитных токов 
и 
. Тогда токи 
создают в окружающем пространстве электромагнитное поле
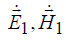, а токи 
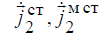– поле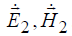 
. Каждое из этих полей связано с возбуждающими их токами своей системой уравнений Максвелла.
Запишем эти две системы и затем умножим скалярно левые и правые части уравнений на векторы 
, как показано в следующих формулах:
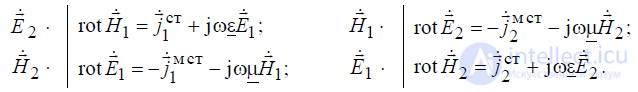
В результате умножения имеем:
Вычитая из верхних равенств нижние, получим:
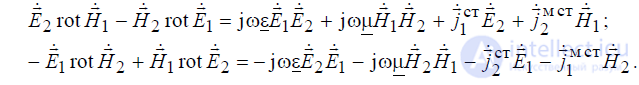
Сложим теперь полученные равенства и воспользуемся известным из век-
торного анализа тождеством (Б.19):
в результате чего получим равенство, которое получило название леммы Ло-
ренца в дифференциальной форме
Окружим обе рассматриваемые области пространства одной поверхно-
стью S (рис.5.3) и проинтегрируем левую и правую части полученного равен-
ства по объему V, ограниченному этой поверхностью:
К левой части равенства (5.12) применим теорему Остроградского-Гаусса,
в результате чего получим лемму Лоренца в интегральной форме, которая
имеет следующий вид:
Соотношения (5.11) и (5.13) достаточно часто используются в теории
ЭМП, в частности при составлении интегральных уравнений для определения распределение электрических токов, наводимых электромагнитным полем на проводящих телах, а также для доказательства некоторых теорем.
Ниже мы с помощью леммы Лоренца докажем теорему взаимности, которая
является важной для теории ЭМП, особенно при решении задач излучения и рассеяния электромагнитных волн.
Рассмотрим бесконечно протяженную изотропную среду с произвольными параметрами ε,μ, σ.
Рисунок 5.4
Зададим в некотором объеме V1 распределение токов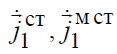 
, а в объеме V2 – 
и применим к данной электромагнитной системе лемму Лоренца.
Для этого окружим оба объема поверхностью
сферы S и устремим ее радиус r → ∞.
Из условия излучения на ∞ поверхностный интеграл в (5.13) стремится к
нулю и от леммы остается равенство:
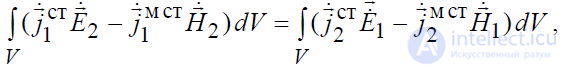, (5.14)
которое представляет собой математическую формулировку теоремы (или принципа) взаимности.
Поясним этот принцип на конкретном примере. Пусть V1 и V2 - это тонкие проводники радиуса a с осевыми токами 
и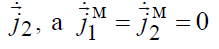 
(рис.5.5). Положим, что расстояние между проводами значительно больше их длин:
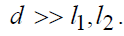
Рисунок 5.5
Тогда оставшийся интеграл в левой части можно расписать, как
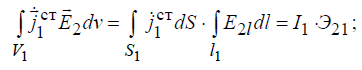
где I1 – ток, текущий в 1-м проводе;Э21 – ЭДС, наведенная в первом проводе полем, созданным током во втором проводе.
Аналогично преобразуем оставшийся интеграл в правой части:
где I2 – ток, текущий в 2-м проводе;Э21 – ЭДС, наведенная в 1-м проводе полем, созданным током во 2-м проводе.
Подставляя в (5.14) найденные значения интегралов, приходим к соотношению:
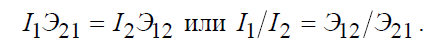. (5.15)
При I1 = I 2 →Э12 = Э21.
Т.о., если среда изотропная, то ток I2 , протекающий во 2-м проводе, наводит в 1-м проводе такую же ЭДС, какую наводит во 2-м проводе ток I1, текущий по первому проводу. Этот принцип является основополагающим в теории антенн. В частности, из него следует, что параметры антенн в режиме приема совпадают с аналогичными параметрами антенн в режиме передачи.
Рассмотрим бесконечное пространство, в котором компактно сосредоточены источники поля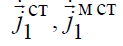 
.
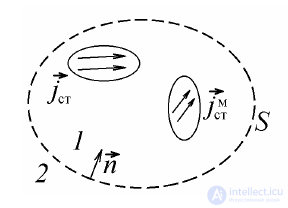
Рисунок 5.6
Чтобы определить поле, создаваемое этими источниками во внешнем пространстве, необходимо решить уравнения Максвелла относительно неизвестных векторов E& r и H& r
. Для однозначного решения этой задачи кроме, распределение источников в пространстве, необходимо знать также граничные условия для тангенциальных компонент электрического либо магнитного поля на границах рассматриваемой области (если они существуют). Вместе с тем на практике часто возникают ситуации, когда сложно задать точное пространственное распределение реальных сторонних источников поля, однако имеется возможность описать поле, которое они создают на некоторой воображаемой замкнутой поверхности S, окружающей эти реальные источники (рис.5.6). Обозначим внутреннюю область пространства с источниками поля (рис.5.6) индексом 1, а внешнюю – индексом 2. Поскольку поверхность S является воображаемой, то поле сторонних источников беспрепятственно проходит из 1 в 2. Вместе с тем, мы можем формально на этой поверхности написать граничные условия для тангенциальных компонент поля.
Для тангенциальной компоненты магнитного поля граничное условие для напряженности магнитного поля на поверхности S с учетом направления вектора нормали nr (рис.5.6) будет иметь вид:
где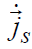 
– поверхностная плотность электрического тока на S.
Перепишем это равенство в виде:
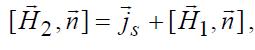, (5.16)
В нашем случае выбранная поверхность является воображаемой, т.е. на самом деле ее не существует, поэтому 0 = sj r
и последнее равенство приобретает вид:
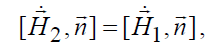, (5.17)
С другой стороны, поле в области 2 не изменилось бы, если мы заменили бы воображаемую поверхность S реальной и к тому же идеально проводящей, на которой бы предположили существование поверхностной плотности тока, найденной из соотношения:
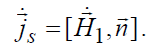. (5.18)
Тогда в равенстве (5.17) мы должны сделать соответствующую замену, в результате чего оно преобразуется к виду:
(5.19)
Условия (5.17) и (5.19) эквивалентны в силу (5.18), поэтому с формальной точки зрения безразлично, какое из этих граничных условий принять во внимание при решении поставленной задачи.
Если выбрать последнее условие, то оказывается, что задачу определения поля во внешней области мы должны сформулировать следующим образом.
Воспользуемся правилом перестановочной двойственности:
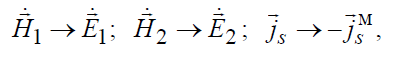
откуда получим граничное условие в случае существования магнитных токов на поверхности S:
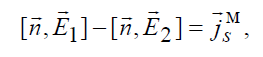
В рассматриваемом случае наша S воображаемая, поэтому никаких токов на поверхности нет. Однако, с формальной математической точки зрения, для определения поля в области 2 нам безразлично, то ли нам известно поле 
на S, то ли токи, задача будет иметь однозначное решение.
На самом деле:
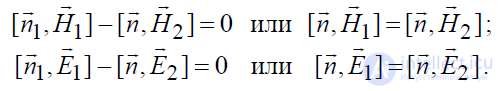
С другой стороны мы можем обозначить: 
и рассмотреть эту задачу в следующей постановке : определить поле во
внешней области 2, если поле в области 1 отсутствует ( 1 Er, 0 1 = Hr), а на поверхности S существуют эквивалентные токи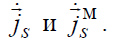 
.
Граничные условия в этом случае сохранятся в виде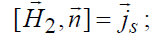 
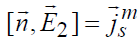
решение задачи вне объема V будет тем же, что и в предыдущем случае. Таким образом, мы перешли от задачи определения поля вне
объема V по известному распределению источников в области 1 к эквивалентной задаче определения того же поля по известному распределению поверхностных токов на поверхности S. Поскольку мы имеем дело только с одним полем, то индексы 2 можно опустить и записать выражение для эквивалентных токов:
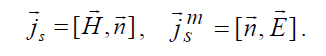. (5.20)
Теперь мы можем сформулировать теорему эквивалентности:
Поле в свободной от источников области пространства не изменится, если реальные источники заменить эквивалентными поверхностными токами
на границе области, а все поля вне этой области положить равными нулю.
Приведенную теорему мы сформулировали на основе простых логических построений. Эту теорему можно доказать строго, используя лемму Лоренца.
Здесь мы получим еще два полезных математических преобразования, известные под названием теорем (или формул) Грина. и чрезвычайно полезным
при различного рода исследований. Эти преобразования следуют непосредственно из теоремы Остроградского-Гаусса:
Введем в рассмотрение две скалярные функции ϕ и ψ, непрерывные в V вместе со своими производными. Образуем с их помощью следующие два вектора: 
. Подставляя один из этих векторов, например 1 A
r
, в формулу (5.21) вместо вектора Ar , получаем выражение:
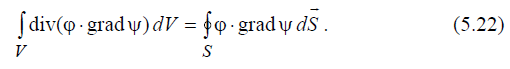
Преобразуем подынтегральную функцию в левой части полученного равенства, используя известное из векторного анализа тождество (Б.19):
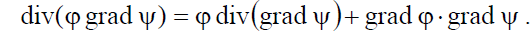
Теперь рассмотрим подынтегральную функцию в правой части равенства
(5.21):
,
где gradn ψ – проекция градиента на нормаль, численно равная производной функции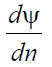 
вдоль направления нормали к поверхности S.
Учитывая сделанные преобразования, нетрудно получить следующее соотношение:
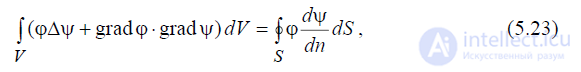
которое представляет собой теорему Грина в 1-й формулировке (или 1-ю формулу Грина).
Теперь вернемся к соотношению (5.21) и подставим в него вектор 2 Ar вместо вектора Ar , а затем выполним над ним те же операции, что были выполнены над вектором 1 A
r
, в результате чего придем к следующему соотношению:
Вычитая из равенства (2.23) равенство (5.24), получаем теорему Грина во 2-й формулировке (или 2-ю формула Грина):
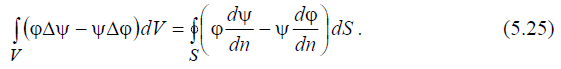
Обе
формулы грина весьма часто применяются для доказательства многих фундаментальных положений электродинамики, а также для получения решений краевых задач электродинамики, сформулированных в виде дифференциальных уравнений.
Исследование, описанное в статье про внутренняя и внешняя задачи электродинамики, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое внутренняя и внешняя задачи электродинамики, теорема о единственности решения внутренней задачи электродинамики, формулы грина и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля