8 Электрический диполь. Электростатическая модель диэлектрика кратко

Привет, Вы узнаете о том , что такое электрический диполь, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электрический диполь, электростатическая модель диэлектрика , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

1. электрический диполь

Электрический диполь — это система из двух равных по величине и противоположных по знаку электрических зарядов +q и -q.
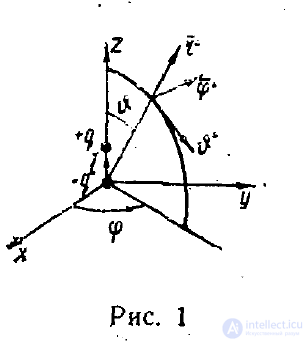
Найдем поле электрического диполя. Для этого вводим сферическую систему координат (рис. 1)
(координату <р не смешивать с потенциалом Согласно изложенному в предыдущей лекции потенциал этой системы равен

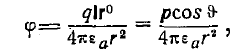
где p = ql — электрический момент диполя.
Напряженность поля равна

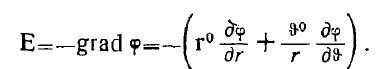
Здесь учтено, что в силу осевой симметрии производная по координате 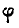равна нулю.

В результате получаем

т. е. составляющие векторы напряженности поля в сферической системе координат; равны

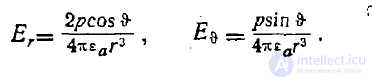
Векторные линии диполя изображены схематически на рис. 2.
Диполь с меняющимся во времени диполыіым моментом является простейшим излучателем радиоволн.

2. Мультиполи

Наряду с диполем можно себе представить более сложные нейтральные системы зарядов, называемые мультиполями.
На рис. 3 изображены диполь, квадруполь и октуполь. Каждый мультиполь, как и диполь, обладает своим моментом:

квадруполь — квадрупольным, октуполь — октупольным моментом.
Бывают мультиполи и более высокого порядка.

Найдем потенциал и момент мультиполя произвольного порядка. Вычисления производятся по той же схеме, по которой вычисляются момент и потенциал диполя
(рис. 4).и не нуждаются в дополнительных пояснениях

Отсюда для потенциала и момента мультиполя /-го порядка находим

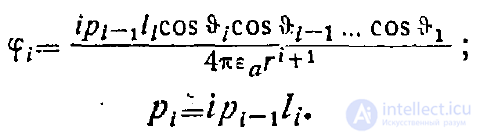
Из формулы для потенциала видно, что поле мультиполя очень быстро убывает с расстоянием по мере повышения его порядка.
Мультнполь может рассматриваться как модель кристаллической решетки. Действительно, кристалл в первом приближении представляют себе как решетку, в узлах которой расположены положительно или отрицательно заряженные ионы атомов.

3. Вектор поляризации

Фа радей впервые заметил, что если между обкладками конденсатора поместить диэлектрик, то происходит увеличение емкости конденсатора, то есть без диэлектрика разность потенциалов опр е д е л я л а с ь формулой
где
qs— заряд на обкладке конденсатора (рис. Об этом говорит сайт https://intellect.icu . 5,а),
—емкость конденсатора и для напряженности поля получалось

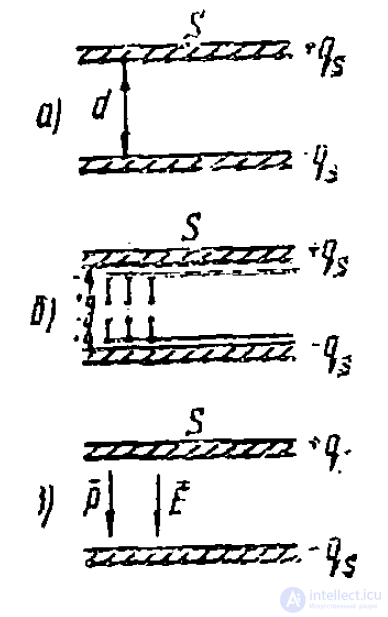
Рис 5
При внесении диэлектрика разность потенциалов вследствие увеличения емкости уменьшается и, следовательно, уменьшается напряженность поля. Этот эффект можно объяснить тем, что под
влиянием электрического поля молекулы вещества диэлектрика поляризуются и в результате на обкладках конденсатора образуется поверхностный заряд противоположного знака первоначальному
поверхностному заряду (рис. 5,6). Так что теперь вместо (1) имеем

(2)

причем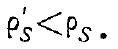

Если ввести в рассмотрение дипольный момент единицы объема Р или, иначе называемый, вектор поляризации, имеющий, как видно
из соотношения

размерность поверхностной плотности зарядов, то можно предположить, что

где Рп— его нормальная к обкладке конденсатора составляющая (рис. 5,в).

Тогда из формулы

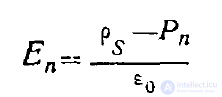
найдем, что

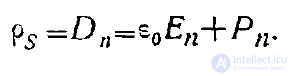
Обобщая, можем написать, что внутри диэлектрика
(3)

Подставив это выраж&ние в третье уравнение Максвелла

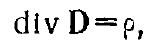
находим

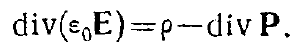
В отличие от р— плотности свободных зарядов — div Р называют плотностью связанных или поляризационных, зарядов, т. е.

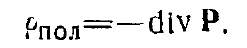
В случае изотропного диэлектрика вектор Р пропорционален вектору Е, т. е.-

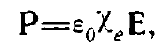(4)
где называется электрической восприимчивостью.

Соответственно

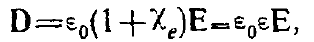
т. е. относительная диэлектрическая проницаемость равна

(5)

Учитывая щхо равенство, вместо (4) можем написать
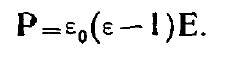. (6)
В случае анизотропного диэлектрика электрическая .восприимчивость является тензором.
Согласна (5) компоненты тензора диэлектрической проницаемости связаны с компонентами тензора электрической восприимчивости формулой

4. Внутреннее поле

Дипольный момент единицы объема равен произведению дипольного момента одной молекулы р м на число молекул N в единице
объема, т. е.

Молекула поляризуется под воздействием поля и поэтому дипольный момент р м должен быть пропорционален напряженности поля. Однако возникает вопрос, какое поле действует на индивидуальную молекулу.

Ведь мы ввели вектор Р в предположении непрерывности вещества диэлектрика. При этом предположении никаких промежутков между молекулами нет. Но в действительности каждая молекула находится в вакууме (е = 1),.хоть она и окружена другими молекулами. Поэтому нельзя ожидать, что то поле, которое индуцирует момент р м , будет равно полю Е, которое получается в предположении непрерывности диэлектрика.
Мы должны, следовательно, считать, что этот момент индуцируется некоторым эффективным полем ЕЭфф так, что

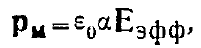
где а — так называемая поляризуемость молекулы, а

Е, — дополнительное «внутреннее» тгале, которое нам надлежит найти.
Итак, каждая молекула находится в некоторой полости внутри диэлектрика.

Самое простое предположение относительно формы полости, которое само собой напрашивается, это то, что эта полость представляет собой шар. Вне этого шара действует вектор поляризации
Р. Значит на поверхности шара действует поляризационный поверхностный заряд плотностью, согласно (3), равной

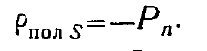
Что означает знак «—»? В случае Ds=os вектор D выходит из положительных зарядов. Следовательно, знак «—» означает, что вектор Р выходит из отрицательных зарядов (рис. 6).

Рис. 6 Рис. 7
Вектор напряженности поля Е/, действующий на молекулу, находящуюся в центре шара, изображен на рис. 7. Эта напряженность поля создается поляризационным поверхностным зарядом плотности

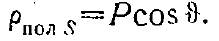
Поле dEi, создаваемое этим поверхностным зарядом, расположенным на элементе

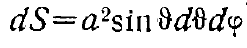
При суммировании векторов поля, создаваемых всеми элементами поверхности шара, останется только вертикальная составляющая поля Eiz (рис. 7 ) , так что необходимо проинтегрировать величину

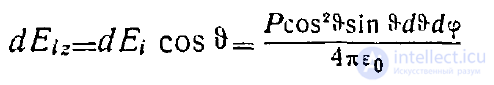
и мы получим

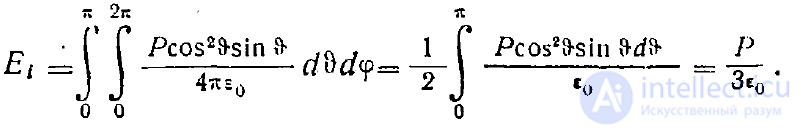
Признаком правильности сделанных предположений и полученного результата является то, что не зависит от радиуса шара.

5. Формула Клаузиуса—Мосотти

Таким образом,

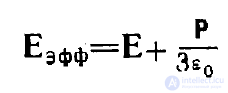
и

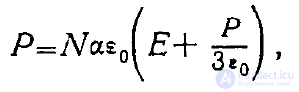
откуда

Учитывая формулу (6), находим

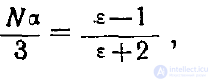(7)
Это соотношение называется формулой Клаузиуса—Мосотти по имени ученых, впервые в середине прошлого века его написавших.
Эта формула примечательна тем, что она связывает между собой макроскопический параметр вещества, каковым является относительная диэлектрическая проницаемость ε , с микропараметрами— поляризуемостью молекулы α и числом N.

Исследование, описанное в статье про электрический диполь, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электрический диполь, электростатическая модель диэлектрика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля

Из статьи мы узнали кратко, но содержательно про электрический диполь