Лекция
Привет, Вы узнаете о том , что такое когерентные волны, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое когерентные волны, некогерентные волны, частично когерентные волны, спектральная когерентность , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Когерентность (от лат. cohaerens — «находящийся в связи») — в физике скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.
Классический пример двух когерентных колебаний — это два синусоидальных колебания одинаковой частоты.
Когерентность волны означает, что в различных пространственных точках волны колебания происходят синхронно, то есть разность фаз между двумя точками не зависит от времени. Отсутствие когерентности, следовательно — ситуация, когда разность фаз между двумя точками не постоянна, а меняется со временем. Такая ситуация может иметь место, если волна была сгенерирована не единым излучателем, а совокупностью одинаковых, но независимых (то есть нескоррелированных) излучателей.
Изучение когерентности световых волн приводит к понятиям временно́й и пространственной когерентности. При распространении электромагнитных волн в волноводах могут иметь место фазовые сингулярности. В случае волн на воде когерентность волны определяет так называемая вторая периодичность.
Без когерентности невозможно наблюдать такое явление, как интерференция.
Радиус когерентности — расстояние, при смещении на которое вдоль псевдо-волновой поверхности, случайное изменение фазы достигает значения порядка π.
Процесс декогеренции — нарушение когерентности, вызываемое взаимодействием частиц с окружающей средой.
Рассмотренные в предыдущих лекциях электрический и магнитный диполи являются простейшими излучателями радиоволн — простейшими антеннами. Одной из важнейших характеристик излучателей волн является направленность излучения. Элементарный вибратор излучает направленно в меридиональных плоскостях. Множителем, характеризующим направленность излучения, или так называемой характеристикой направленности здесь является 
. В экваториальной плоскости элементарный вибратор излучает ненаправленно. Мы видим, что направленность излучения одиночного электрического или одиночного магнитного диполей либо весьма слабая, либо отсутствует вовсе. Наглядное представление о направленности излучения этих элементарных излучателей могут дать их диаграммы направленности.
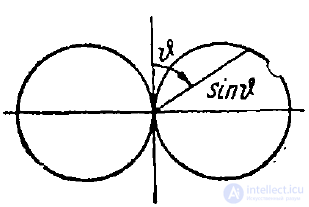
рис. 1
На рис. 1 изображена диаграмма направленности излучения диполя в меридиональной плоскости. Она представляет собой кривую функции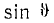 
в полярных координатах. Диаграмма направленности излучения в экваториальной плоскости представляет собой окружность. Излучение высокой направленности может создать лишь система излучателей даже ненаправленных, но должным образом расположенных и сфазированных. Покажем это па примере двух элементарных вибраторов.
Итак, рассмотрим поле системы двух элементарных параллельных вибраторов в их экваториальной плоскости.
Пусть вибраторы 1, 2 разнесены па расстоянии 
(рис. 2), причем колебания тока вибратора 2 опережают по фазе ток вибратора t на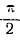 
.
Поля вибраторов соответственно равны
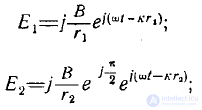
где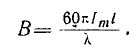 
Рис. 2
Для удаленной точки наблюдения, т. е. при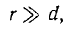 
, можно считать
В фазовых же множителях разностью расстояний r2 и r1 пренебречь нельзя, однако лучи от вибраторов до точки наблюдения M можно считать параллельными и тогда
Складывая поля, с учетом последних равенств получаем
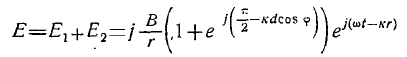
и, поскольку
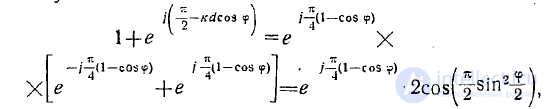
для амплитуды напряженности поля получаем
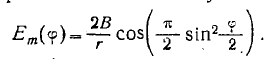
Таким образом, характеристикой направленности здесь является функция
. ,
Отсюда видно, что
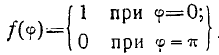
т. е. эта система излучает однонаправленно.
График функции или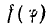 
иначе диаграмма направленности в полярной системе координат изображена на рис. 3.
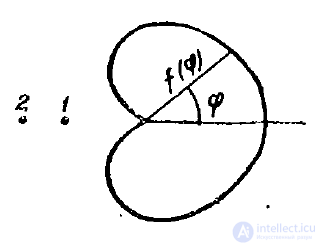
Рис. 3
Из приведенного примера можно сделать вывод, что с помощью большого числа элементарных излучателей, соответствующим образом расположенных и сфазнрованных, можно создать антенну и более высокой направленности. Ясно, что направленное излучение оказывается возможным создать благодаря явлению интерференции волн. Об этом говорит сайт https://intellect.icu . Поэтому нужно установить, при каких условиях возможна интерференция волн.
В зависимости от величин 
, q и Ψ ДН системы связанных вибраторов могут иметь различную форму (рис. 3a)
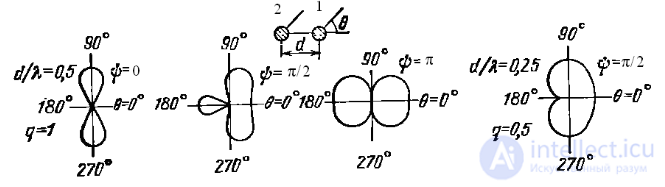
Рис. 3a Нормированные ДН по напряженности поля системы связанных вибраторов в экваториальной плоскости
При увеличении расстояния между вибраторами (начиная от =0,5) ДН приобретает многолепестковый характер; чем больше , тем больше лепестков. Особенно важен случай однонаправленного излучения.
Рассмотрим два колебания тока на одной и той же частоте с постоянными амплитудами и начальными фазами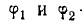 
:
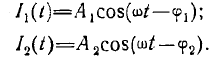
Суммарное колебание равно
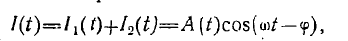
причем
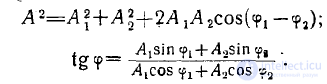(1)
Обратим внимание на два крайних случая.
1. Разность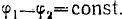 
. В этом случае колебания когерентны.
2. Фазы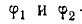 
— случайные функции времени.
Фазу как случайную функцию времени можно себе представить следующим образом. Через каждый промежуток времени т фаза меняется скачком, принимая случайное значение. В результате, если усредним (1) по интервалу времени, значительно большем т, то получим
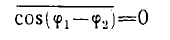(2)
и
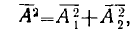
где черта сверху означает среднее, значение. Такие два колебания, для которых имеет место (2), являются некогерентными. Заметим, что фазы обоих колебаний могут быть случайными функциями времени, но при этом
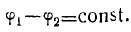
В этом случае колебания также будут когерентными.
Рассмотрим сферические волны, создаваемые элементарным вибратором с током, начальная фаза колебания которого меняется, через каждый промежуток времени т скачком, принимая случайные значения. Величина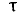 
называется временем когерентности. Нас будет интересовать вопрос: когерентны ли колебания поля, создаваемые этим источником в разных точках пространства?
Если из источника как центра провести сферу радиуса г1, то эту поверхность будут пересекать так называемые цуги волн, длительность которых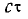 
. Величина 
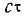называется длиной когерентности.
В течение времени т начальные фазы колебаний в любой точке сферы будут одинаковы. По истечении этого промежутка времени фаза во всех точках меняется на одну н ту же случайную величину.
Проведем другую сферу радиуса r2. Выясним, когда колебания на-этих двух сферах будут когерентными и когда они некогерентны.
Очевидно, что если
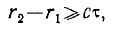
то колебания будут некогерентны. • •
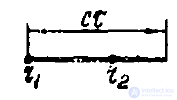
Рис. 4
Если же
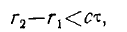
то в этом случае колебания будут когерентны в течение времени (рис. 4)
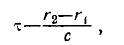
т. е. не в течение всего промежутка времени t, а только части его. В виду этого колебания называются частично когерентными.
Ясно, что колебания поля в каких-либо точках, находящихся на одной и той же сфере, будут всегда когерентными.
Таким образом, по мере того, как разность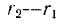 
уменьшается, колебания от некогерентных переходят в частично когерентные и затем при 
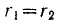становятся когерентными.
Понятие временно́й когерентности можно связать с контрастом интерференционной картины, наблюдаемой в результате интерференции двух волн, исходящих из одной и той же точки поперечного сечения пучка (полученных методом деления амплитуд). Временна́я когерентность волны характеризует сохранение взаимной когерентности при временном отставании одного из таких лучей по отношению к другому. При этом мерой временной когерентности служит время когерентности — максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность еще сохраняется. Временная когерентность определяется степенью монохроматичности.
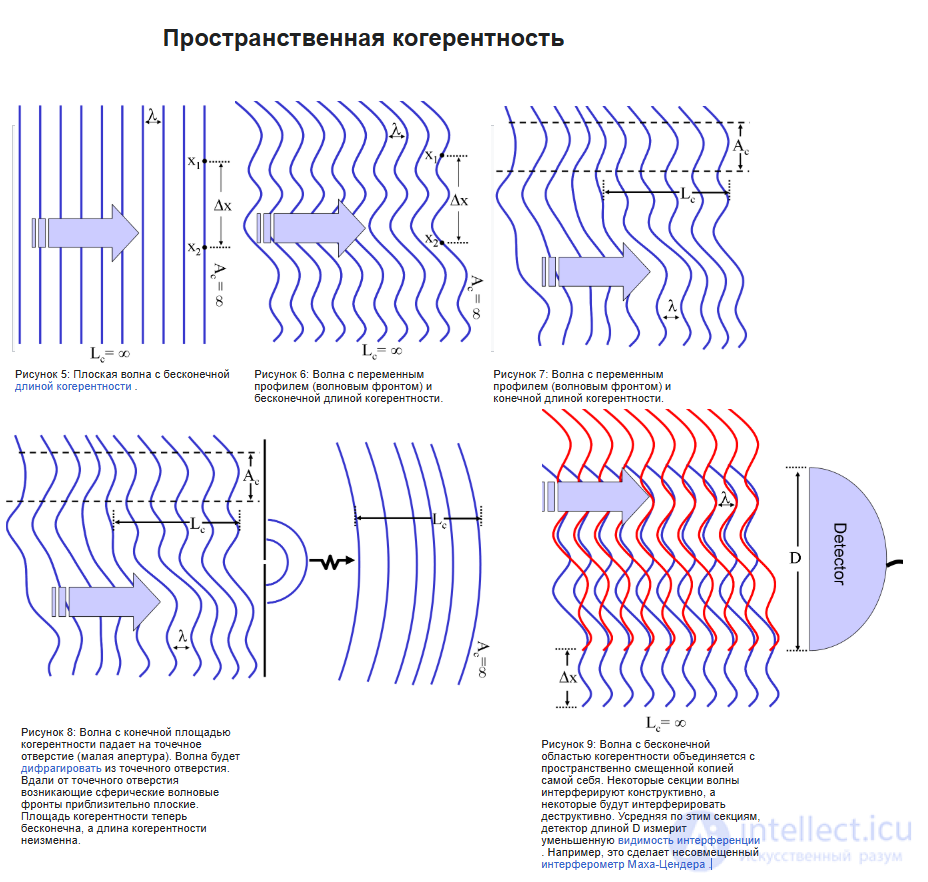
Пространственная когерентность — когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости, перпендикулярной направлению распространения волны.
Понятие пространственной когерентности введено для объяснения явления интерференции (на экране) от двух разных источников (от двух точек удлиненного источника, от двух точек круглого источника и т. п.).
Так, при определенном расстоянии от источников разность оптического хода будет такой, что фазы двух волн будут отличаться. В результате этого приходящие волны от различных частей источника в центр экрана будут уменьшать значение мощности по сравнению с максимальным, которое имело бы место, если бы все волны имели одинаковую фазу. На расстоянии, где разность оптического хода приведет к тому, что фазы двух волн будут различаться ровно на π, сумма двух волн будет минимальна
Рассмотрим теперь суперпозицию волн, создаваемых двумя разнесенными . элементарными вибраторами в экваториальной плоскости. Здесь возможны следующие случаи.
Если разность фаз токов обоих вибраторов постоянная величина, то разность фаз волн, приходящих в каждую точку пространства от обоих вибраторов, сохраняется все время и волны будут когерентными.
В этом случае, мы видели, имеет место явление интерференции. Если разность колебаний токов у обоих вибраторов является случайной величиной, то в каждой точке пространства колебания поля, сздаваемые каждым вибратором, будут некогерентными и волны будут некогерентными. Интерференции не будет.
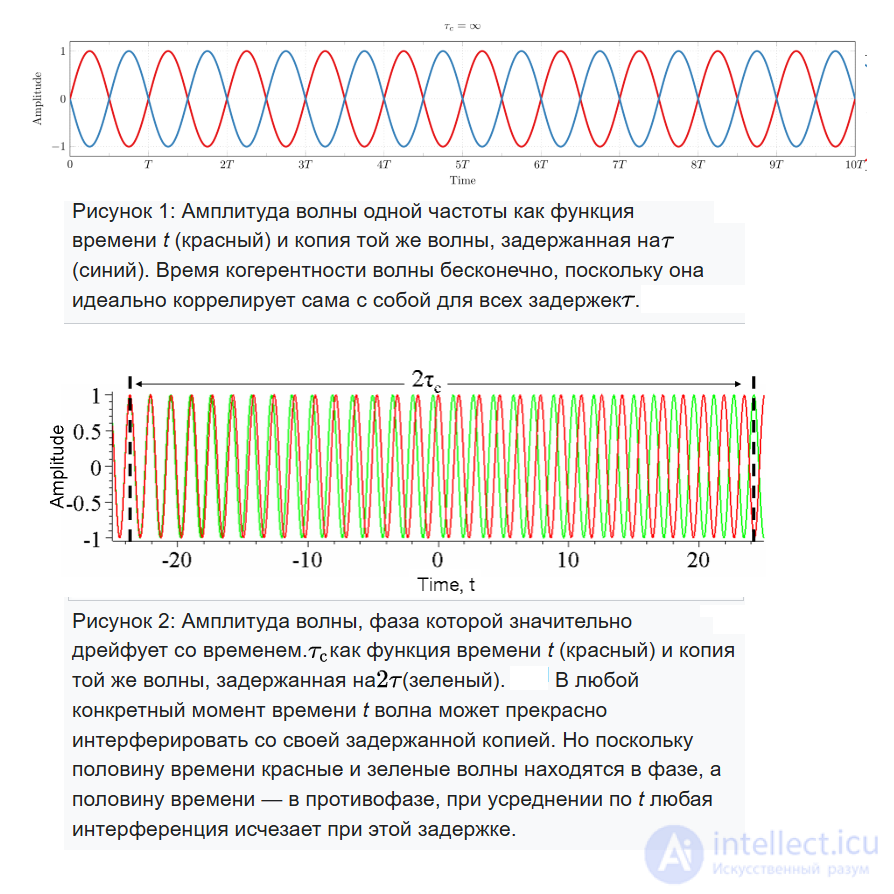
Пусть теперь второй вибратор является зеркальным изображением первого вибратора, создающим отраженные от зеркала волны, и пусть фаза тока в этом вибраторе меняется указанным выше случайным образом.
Очевидно, что прямые и отраженные волны будут в соответствии с изложенными в пункте 3 когеренты или частично когерентны, если они принадлежит одному и тому же цугу волн. Такого рода когерентность называется временной. Реальный источник волн в действительности не точный. Однако, если источник имеет достаточно малую пространственную протяженность, то он совместно со своим зеркальным изображением может создать четкую интерференционную картину. Источник, удовлетворяющий этому условию, .называется пространственно когерентным. Два пространственно когерентных источника волн в произвольных точках, вообще говоря, создают некоге.рентные или частично когерентные колебания. Колебания в двух точках будут когерентными только в том случае, если разность расстояний от одного источника
к этим точкам минус разность расстояний от другого источника к тем же двум точкам, равна целому числу длин волн.
Голография требует свет с большим временем когерентности. Напротив, оптическая когерентная томография , в своей классической версии, использует свет с коротким временем когерентности.
Волны разных частот (на свету это разные цвета) могут интерферировать, образуя импульс, если они имеют фиксированное относительное фазовое соотношение (см. преобразование Фурье ). И наоборот, если волны разных частот не когерентны, то при объединении они создают волну, непрерывную во времени (например, белый свет или белый шум ). Временная длительность импульса 
ограничено спектральной шириной полосы света 
в соответствии с:
,
что следует из свойств преобразования Фурье и приводит к принципу неопределенности Кюпфмюллера (для квантовых частиц это также приводит к принципу неопределенности Гейзенберга ).
Если фаза линейно зависит от частоты (т.е. 
) тогда импульс будет иметь минимальную длительность для своей полосы пропускания ( импульс с ограничением по преобразованию ), в противном случае он будет чирпированным (см. дисперсию ).
Для измерения спектральной когерентности света требуется нелинейный оптический интерферометр, например, оптический коррелятор интенсивности , частотно-разрешенное оптическое стробирование (FROG) или спектральная фазовая интерферометрия для прямой реконструкции электрического поля (SPIDER).
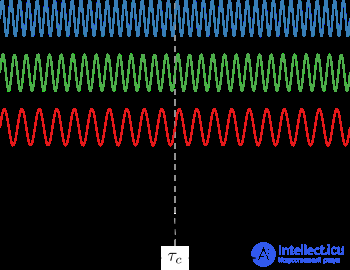
Рисунок 10: Волны разных частот интерферируют, образуя локализованный импульс, если они когерентны.
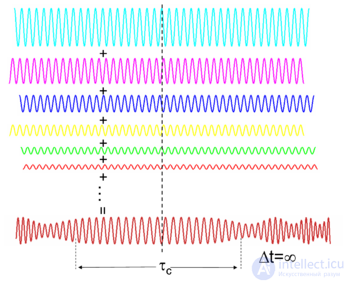
Рисунок 11: Спектрально некогерентный свет интерферирует, образуя непрерывный свет со случайно изменяющейся фазой и амплитудой.
Исследование, описанное в статье про когерентные волны, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое когерентные волны, некогерентные волны, частично когерентные волны, спектральная когерентность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля