Лекция 11 мин.
Привет, Вы узнаете о том , что такое поля вибратора, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое поля вибратора, вибратор герца, симметричный вибратор, диполь герца , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
Элементарным вибратором называют элемент проводника, по которому протекает переменный во времени ток, одинаковый по всем сечениям проводника в каждый фиксированный момент времени (рис. 1,а). Практической реализацией элементарного вибратора может служить
диполь герца . Диполь Герца представляет собой два соединенных проводом металлических шара, заряды которых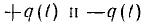 
в каждый момент времени одинаковы по величине и противоположны по знаку (рис. 1.6).
Рис. 1
вибратор герца ( симметричный вибратор , диполь Герца) — простейшая антенна, устройство для излучения и приема электромагнитных волн. Представляет собой относительно короткий (по сравнению с длиной волны) прямолинейный электрический проводник с разрывом посередине, питаемый (в режиме излучения) в точках разрыва генератором тока высокой частоты. Первые эксперименты с подобной антенной были осуществлены Генрихом Герцем в 1886—1888 годах. В электродинамике под диполем Герца понимают модель в виде элемента (короткого фрагмента) прямолинейного переменного электрического тока малой длины с постоянными по всей длине амплитудой и фазой колебаний/ Если после зарядки диполя предоставить его самому себе, то возникнут колебания, поскольку шары, соединенные проводом, обладают емкостью и индуктивностью и неизбежным сопротивлением, которое приводит к затуханию этих колебаний.
Силовые линии электрического (синие) и магнитного (красные) полей вблизи излучающего вибратора малой длины. Плотность потока электромагнитной энергии максимальна в направлениях, лежащих в плоскости перпендикулярной вибратору
По проводу, соединяющему оба шара, потечет ток
(1)
в каждый фиксированный момент одинаковый по всем сечениям провода (рис. 1,6).
Диполь Герца имеет дипольный момент, меняющийся во времени:
где / — длина диполя
Соответственно дипольным моментом p(t) обладает любой элементарный вибратор, причем этот момент и ток I (t) в вибраторе связаны формулой
которая в случае гармонической зависимости тока от времени преобразуется к виду
С учетом изложенного элементарный вибратор называют диполем Герца или просто электрическим диполем.
Достаточно короткий элемент провода длины / любой проводной антенны может рассматриваться как элементарный вибратор, если эта длина значительно меньше излучаемой Длины волны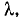 
, т. е.
(2)
Пусть ток в элементарном вибраторе, расположенном в начале координат (рис. 2), меняется по гармоническому закону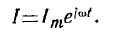 
Найдем поле этого вибратора. Его векторный потенциал А согласно (8)лекци и 19 и в силу (2) равен
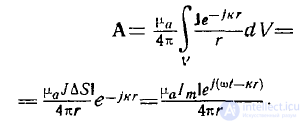(3)
Рис. Об этом говорит сайт https://intellect.icu . 2
Из этого выражения, видно, что векторный потенциал А параллелен вектору I . Это обстоятельство значительно упрощает расчет вектора электромагнитного поля."
Применяем сферическую систему координат г, Ь, ср. В этой системе координат, как видно из рис. 2, составляющие вектора А равны
Выясним сначала, какие составляющие векторов поля Е и H отличны от нуля, а какие равны нулю. Для этого обратимся к формулам
В сферической системе координат составляющие вектора при наличии осевой симметрии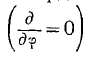 
таковы
(6)
Сопоставляя между собой формулы (4) — (6), заключаем, что
т. е. вектор H имеет только одну «экваториальную» составляющую 
а вектор Е — радиальную и «меридиональную» составляющие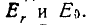 
Составляющие вектора Е можно вычислить по вектору А двумя способами: по формулам (4) и (5) или, пользуясь ' условием Лорентца, по формулам
Нетрудно убедиться в том, что оба способа приводят к одному и тому же результату. В самом деле, согласно (4) и (5),
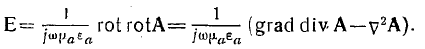
Учитывая волновое уравнение для вектора А
имеем
что и требовалось доказать
Пользуясь соотношениями (6), вычисления составляющих поля выполним первым способом.
В результате получим следующие точные формулы для составляющих векторов поля:
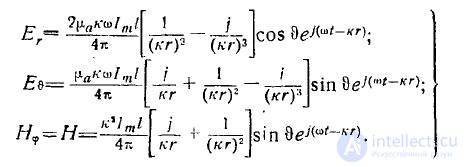(7)
Пользуясь формулой (2), введем в эти выражения дипольный момент 
и представим их в виде
(8)
Как видно из формул (7) или (8), составляющие векторов поля элементарного вибратора характеризуются суммой слагаемых, различным образом зависящих от расстояния. В связи с этим в пространстве, окружающем вибратор, можно выделить три зоны — ближнюю, промежуточную и дальнюю, или волновую, зоны. Эти зоны определяются условиями:
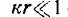— ближняя зона;
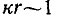— промежуточная зона;
— дальняя зона элементарного вибратора.
Рассмотрим ближнюю зону 
В этой зоне основной вклад в поле вносят слагаемые, содержащие высшие степени — . Пренебрегая слагаемыми более низких / кг степеней, по формулам (8) и (7) находим
(9)
(10)
Согласно формулам (9) электрическое поле элементарного вибратора в ближней зоне по величине поля в каждый момент времени и конфигурации его векторных линий — это электростатическое поле диполя, но с меняющимся во времени дипольным моментом. Согласно (10) магнитное поле элементарного вибратора в ближней зоне по конфигурации векторных линий ноля и по его величине— это магыптостатическое поле, определяемое законом Био и Савара, но ток, создающий это поле, Меняется во времени.'Как видим по формулам (9) и (10) вблизи впбратораі пренебрегается запаздывание, поэтому здесь поле называется квазистацнопариым.-
Рассмотрим волновую зону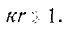 
В этой зоне основной вклад в величину поля вносит слагаемое с первой степенью 1/кг
Поэтому, пренебрегая слагаемыми степеней ~jr более высокого порядка, получаем
(11 )
Анализ выражений (11) позволяет сделать следующие выводы относительно электромагнитного поля в дальней зоне:
1) векторы Е и H как и в плоских волнах взаимно перпендикулярны;
2) поверхности равных фаз представляют собой сферы, т. е. волна сферическая;
3) скорость распространения волны, как в случае плоских волн, равна
4) вектор скорости ѵ перпендикулярен векторам Е и Н, в силу чего волны эти поперечны, как в случае плоских волн;
5) величины Е и H меняются во времени еннфазно;
6) амплитуды напряженностей поля обратно пропорциональны расстоянию 1/r;
7) амплитуды напряженностей поля зависят от угла 
, и поскольку они пропорциональны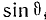 
, то поле максимально в экваториальной плоскости и равно нулю вдоль оси вибратора, т. е. элементарный вибратор, излучает волны направленно;
8) амплитуды пропорциональны величине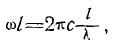 
т. е. отношению длины вибратора к длине волны;
9) отношение напряженностей Е и Н, как и в случае плоских волн, равно волновому сопротивлению среды, т. е.
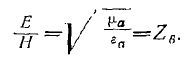
Напряженности поля элементарного вибратора в дальней зоне в свободном пространстве, где
равны
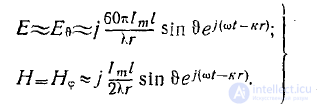(12)
В зависимости от отношения длины вибратора к длине волны и места включения к нему фидера его диаграмма направленности принимает вид, изображенный на рисунке:
| Отношение длины вибратора к длине волны |
КНД, дБи | Примечание |
|---|---|---|
| ≪0,5 | 1,76 | низкая эффективность |
| 0,5 | 2,15 | наиболее распространенный |
| 1,0 | 4,0 | только с толстыми вибраторами |
| 1,25 | 5,2 | наибольшее усиление |
| 1,5 | 3,5 | третья гармоника |
| 2,0 | 4,3 | не используется |
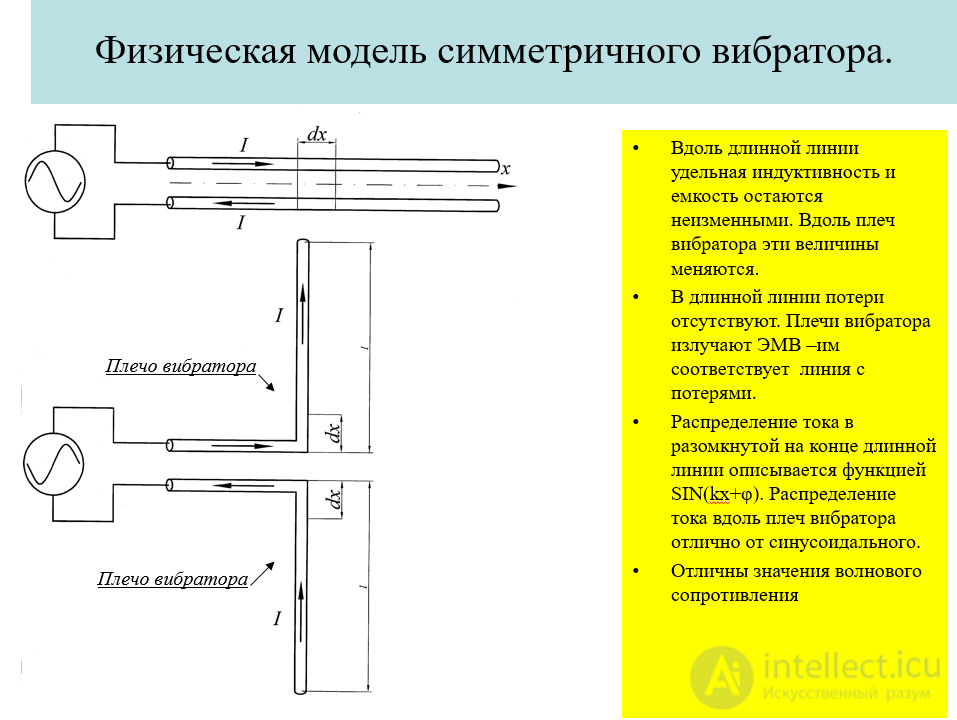
Физическая модель симметричного вибратора.
Формирование поля симметричным вибратором.
Распределение тока по плечам вибратора. Волновое сопротивление
Определение поля симметричного вибратора в дальней зоне.
Диаграмма направленности симметричного вибратора.
Диаграммы направленности симметричного вибратора в плоскости Е.
Сопротивление излучения симметричного вибратора.
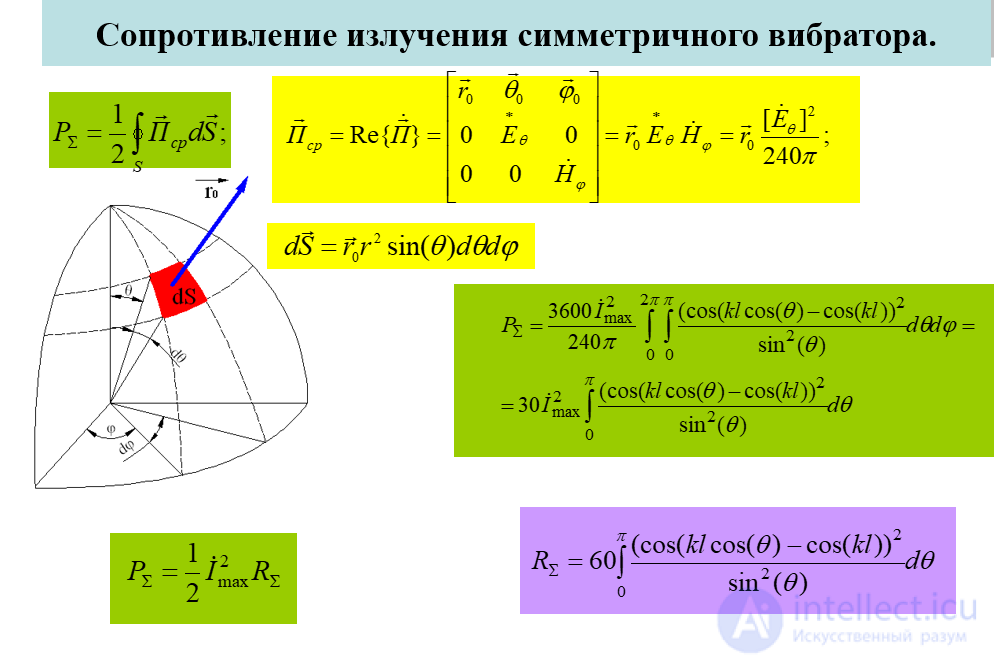
Зависимость сопротивления излучения от соотношения длины волны λ и длины плеча вибратора l.
Определение входного сопротивления антенны
Распределение тока вдоль плеч вибратора. Метод интегрального уравнения.
Четвертьволновый симметричный вибратор. Укорочение для настройки в резонанс.
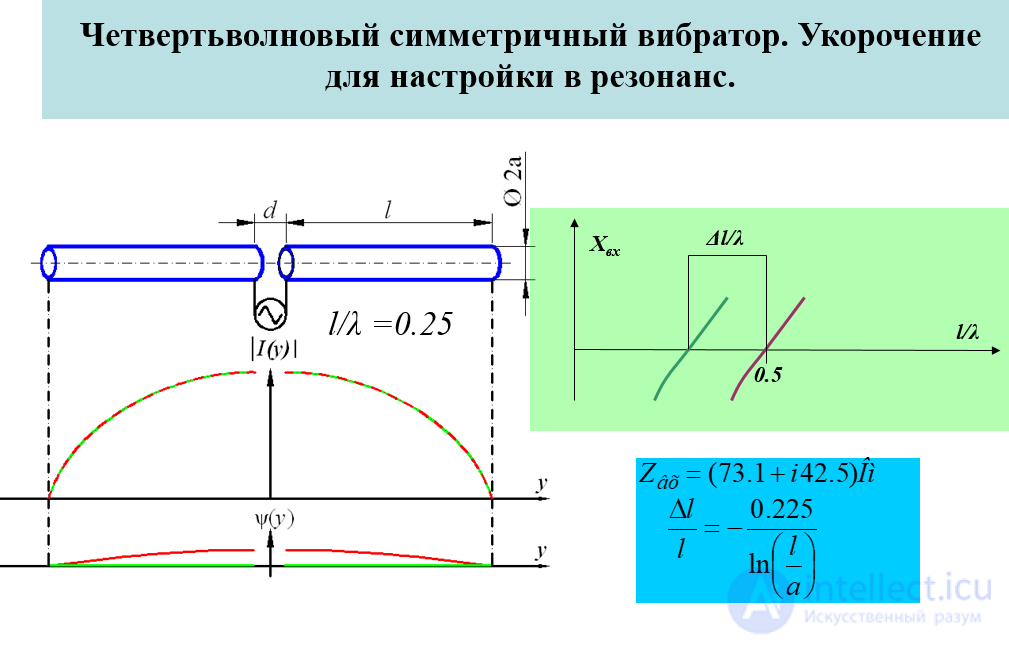
Расчет входного сопротивления с учетом потерь в эквивалентной длинной линии
Действующая длина симметричного вибратора.
Исследование, описанное в статье про поля вибратора, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое поля вибратора, вибратор герца, симметричный вибратор, диполь герца и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Из статьи мы узнали кратко, но содержательно про поля вибратора
Комментарии