Лекция
Привет, Вы узнаете о том , что такое закон сохранения заряда, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон сохранения заряда , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
В физике и теории электромагнитного поля сохранение заряда — это принцип экспериментального характера, согласно которому общий электрический заряд в изолированной системе никогда не меняется. Чистое количество электрического заряда, количество положительного заряда за вычетом количества отрицательного заряда во Вселенной, всегда сохраняется . Сохранение заряда, рассматриваемое как физический закон сохранения , подразумевает, что изменение количества электрического заряда в любом объеме пространства в точности равно количеству заряда, втекающего в объем, за вычетом количества заряда, вытекающего из объема. По сути, сохранение заряда — это учетное соотношение между количеством заряда в области и потоком заряда в эту область и из нее, заданное уравнением непрерывности между плотностью заряда ρ(х) и плотность тока .
Это не означает, что отдельные положительные и отрицательные заряды не могут быть созданы или уничтожены. Электрический заряд переносится субатомными частицами , такими как электроны и протоны . Заряженные частицы могут создаваться и уничтожаться в реакциях элементарных частиц. В физике элементарных частиц сохранение заряда означает, что в реакциях, создающих заряженные частицы, всегда создается равное количество положительных и отрицательных частиц, сохраняя чистое количество заряда неизменным. Аналогично, когда частицы уничтожаются, уничтожается равное количество положительных и отрицательных зарядов. Это свойство подтверждается без исключения всеми эмпирическими наблюдениями до сих пор.
Хотя сохранение заряда требует, чтобы общее количество заряда во Вселенной было постоянным, оно оставляет открытым вопрос о том, каково это количество. Большинство свидетельств указывают на то, что чистый заряд во Вселенной равен нулю; то есть существуют равные количества положительного и отрицательного заряда.
Сохранение заряда было впервые предложено британским ученым Уильямом Уотсоном в 1746 году и американским государственным деятелем и ученым Бенджамином Франклином в 1747 году, хотя первое убедительное доказательство было дано Майклом Фарадеем в 1843 году.
Теперь открыто и доказано, как здесь, так и в Европе, что Электрический Огонь — это реальный Элемент, или Вид Материи, не созданный Трением, а только собранный .
— Бенджамин Франклин, Письмо Кэдвалладеру Колдену, 5 июня 1747 г.
Рассмотрим тело объемом V (рис.2.1), содержащее в себе электрические заряды, суммарная величина которых равна Q. Об этом говорит сайт https://intellect.icu . Пусть эти заряды постепенно выходят наружу, проникая через ограничивающую тело поверхность S.
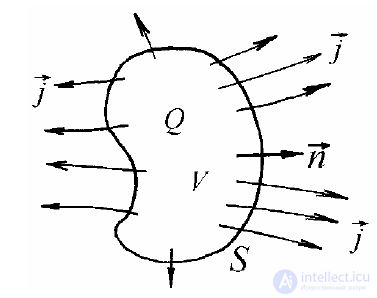
Рисунок 2.1
В этом случае можно говорить, что через поверхность S протекает ток
 . (2.1)
. (2.1)
Если выразить левую и правую части данного равенства через объемные плотности тока и заряда, то нетрудно придти к следующему равенству:
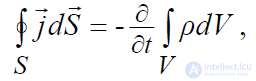 (2.2)
(2.2)
которое представляет собой
закон сохранения заряда в интегральной форме.
Применим к левой части полученного равенства теорему Гаусса-Остроградского:
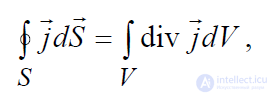 ,
,
что дает право его записать в виде
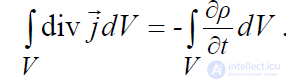 .
.
Теперь перенесем все члены равенства в левую его часть и объединим их под знаком одного интеграла, что дает следующее выражение:
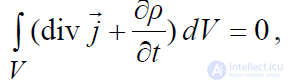
откуда следует равенство:
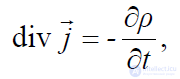 (2.3)
(2.3)
которое является математическим выражением закона сохранения заряда в дифференциальной форме, больше известного как уравнение непрерывности.
В словесной форме закон сохранения заряда формулируется следующим образом:
Всякому изменению величины заряда, сосредоточенного внутри некоторой области пространства, соответствует электрический ток, вытекающий из этой области или втекающий в нее.
Закон сохранения зарядов можно рассматривать как следствие уравнений Максвелла. Действительно, если во втором уравнении Максвелла контур / стянуть в точку, то получим, что контурный интеграл будет равен нулю, поверхность S окажется замкнутой
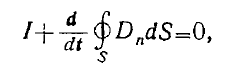
Воспользовавшись третьим уравнением, находим, что
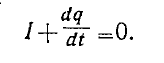
Это соотношение формулирует закон сохранения заряда. Изменение зарядов внутри некоторого объема, ограниченного замкнутой поверхностью, равно току, протекающему через эту поверхность.
Если в первом уравнении Максвелла стянуть контур в точку, то контурный интеграл будет равен нулю, поверхность S окажется
замкнутой и мы получим

то есть
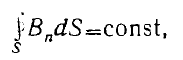
причем согласно четвертому уравнению
const = 0.
Таким образом, из второго и третьего уравнений Максвелла вытекает закон сохранения электрических зарядов, а из первого и четвертого уравнений вытекает закон сохранения своего рода
«магнитных зарядов», т. е. всегда действует суммарный «магнитный заряд», равный нулю.
Иначе говоря, в природе не существует магнитных зарядов, аналогичных электрическим.
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объеме равно полному току через поверхность, можно записать в математической форме:
Здесь Ω — некоторая произвольная область в трехмерном пространстве, ∂Ω — граница этой области, ρ — плотность заряда, — плотность тока (плотность потока электрического заряда) через границу.
Переходя к бесконечно малому объему и используя по мере необходимости теорему Остроградского — Гаусса, можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности):
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается, что электронная система не может значительно изменять свой суммарный заряд.
Исследование, описанное в статье про закон сохранения заряда, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое закон сохранения заряда и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Из статьи мы узнали кратко, но содержательно про закон сохранения заряда
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля