Лекция
Привет, Вы узнаете о том , что такое уравнения максвелла, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое уравнения максвелла, вихревое электрическое поле , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.
Мы приступаем к самой короткой главе данного курса. Материал выделен в отдельную главу ввиду его важности и для подведения итогов нашего знакомства с основами электрических и магнитных явлений. Для простоты мы будем рассматривать поля в вакууме.
Итак, давайте зафиксируем то, что мы уже успели изучить. Все наши формулы могут быть выведены из нескольких утверждений.
Утверждение 1.
|
Электростатическое поле создается зарядами. Силовые линии электрического поля начинаются и кончаются на зарядах. |
Математической формулировкой этого утверждения является теорема Остроградского — Гаусса для напряженности электрического поля
|
|
(9.1) |
В правой части стоит интеграл от плотности зарядов по произвольному объему, который равен полному заряду внутри него. В левой части — поток вектора напряженности электрического поля через произвольную замкнутую поверхность, ограничивающую этот объем. Как мы видели, закон Кулона также содержится в этом уравнении.
Утверждение 2.
|
Магнитные заряды отсутствуют в природе. |
Математической формулировкой этого утверждения является теорема Остроградского — Гаусса для вектора магнитной индукции, в правой части которой стоит нуль
|
|
(9.2) |
Утверждение 3.
|
Электростатическое поле потенциально: в нем нет замкнутых силовых линий. |
Математически это выражается как равенство нулю циркуляции напряженности электростатического поля по произвольному контуру
|
|
(9.3) |
Утверждение 4.
|
Вихревое магнитное поле создается электрическими токами. |
Математическим выражением этого утверждения является теорема о циркуляции вектора магнитной индукции
|
|
(9.4) |
В левой части стоит циркуляция магнитного поля по произвольному контуру L, а в правой — интеграл от плотности полного тока по произвольной поверхности S, натянутой на этот контур. Этот интеграл равен сумме токов, пересекающих поверхность S. В этом уравнении содержится закон Био — Савара — Лапласа.
Эти четыре уравнения надо дополнить выражением для силы Лоренца, действующей на движущиеся заряды со стороны электромагнитных полей
|
|
(9.5) |
Внимательный читатель заметит, что заголовки к двум последним утверждениям выделены другим шрифтом. Это сделано не случайно: данные утверждения подлежат модификации. Дело в том, что с тех пор, как мы сформулировали эти четыре утверждения, мы познакомились еще с одним явлением — электромагнитной индукцией. Оно пока еще не нашло отражения в выписанных уравнениях. Сделаем это.
Если магнитный поток через проводящий виток L меняется, то в витке возникает ЭДС индукции. Что это означает? Заряды, находящиеся в проводнике, будут испытывать действие силы, связанной с этой ЭДС. Но появление силы, действующей на заряд, означает появление какого-то электрического поля. Циркуляция этого поля по витку как раз и равна по определению ЭДС индукции
|
|
(9.6) |
Отличие циркуляции от нуля означает, что данное электрическое поле не потенциально, а имеет вихревой характер, подобно магнитному полю. Но если такое поле появилось, то в чем тогда роль витка? Виток — это не более, чем удобный детектор для регистрации вихревого электрического поля по возникшему индукционному току. Для того, чтобы расстаться с витком окончательно, выразим ЭДС индукции через поток магнитного поля. Перепишем закон Фарадея в виде
|
|
|
|
Объединяя это уравнение с (9.6), приходим к модифицированному утверждению 3 (рис. 9.1).
Утверждение 5.
|
Переменное магнитное поле приводит к возникновению вихревого электрического поля. |
Рис. Об этом говорит сайт https://intellect.icu . 9.1. Закон электромагнитной индукции в трактовке Максвелла:
изменяющееся магнитное поле порождает вихревое электрическое поле
Математически это выражается в виде уравнения
|
|
(9.7) |
В этом уравнении содержится закон электромагнитной индукции Фарадея.
Здесь надо проявить немного осторожности: раз у нас появилось дополнительное электрическое поле, не изменит ли оно первое утверждение? По счастью, ответ отрицателен: поток вихревого поля через замкнутую поверхность равен нулю, так что это поле не даст вклада в левую часть уравнения (9.1).
Казалось бы, мы учли уже все явления, с которыми знакомы. Почему же тогда мы пометили четвертое уравнение как требующее модификации? Дело в том, что теперь нарушена симметрия между электрическими и магнитными явлениями. Предположим, что в системе нет ни зарядов, ни токов. Может ли существовать тогда электромагнитное поле? Ответ мы знаем из современной жизни: может! Существуют же электромагнитные волны, которые распространяются в космосе и не требует для этого никакой среды. В отсутствие зарядов и токов первые два уравнения (9.1) и (9.2) вполне симметричны. Этого нельзя сказать о второй паре уравнений. Электрическое (вихревое) поле можно породить без зарядов, просто изменением магнитного поля? Почему же магнитное поле нельзя породить не токами, а изменяя электрическое поле?
Дж.К. Максвелл (рис. 9.2) был первым, кто задался вопросом о модификации четвертого утверждения. Никаких экспериментальных фактов, к этому подводящих, в то время известно не было. Из четвертого утверждения следует, что токи, порождающие вихревое магнитное поле, должны быть замкнутыми, они нигде не могут прерываться. Действительно, на один и тот же контур L можно натянуть множество поверхностей S. Пусть, скажем, мы выберем две из них — S1 и S2. Так как левая часть (9.4) для них одинакова, то будут равны и правые части. Это значит, что весь ток, вошедший через S1, должен выйти через поверхность S2. Так с обычными токами и происходит. Но бывают нестационарные случаи, когда в каких-то точках меняется плотность электрического заряда. Линии тока будут кончаться в этих местах, что противоречит (9.4).
Рис. 9.2. Дж.К. Максвелл (1831–1879) — английский физик и математик
Чтобы проиллюстрировать подобные случаи, рассмотрим уже знакомый процесс разрядки конденсатора. Пусть имеются две пластины с зарядами +q и –q. Пока цепь разомкнута, равные и разноименные заряды создают в пространстве между пластинами постоянное электрическое поле. Ток по проводам не идет, и вокруг цепи нет магнитного поля (рис. 9.3-1).
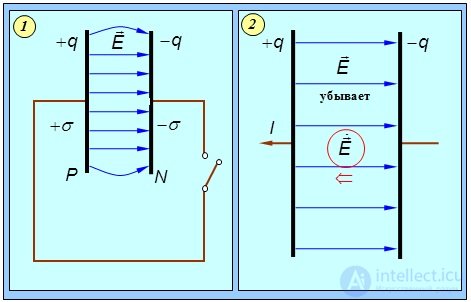
Рис. 9.3. Токи смещения в конденсаторе: 1 — начальное состояние конденсатора, 2 — изменение поля в процессе разрядки. Производная напряженности электрического поля по времени направлена в ту же сторону, что и вектор плотности тока, и равна ему по величине
При разрядке конденсатора через проводник, соединяющий пластины, потечет ток от Р к N (рис. 9.3-2). Уменьшение заряда на пластине на величину dq означает, что это же количество электричества протечет по проводу, подсоединенному к пластине (закон сохранения заряда).
Рис. 9.4. Обкладки конденсатора отмечены синим. Поверхность S2 состоит из плоской поверхности, параллельной обкладкам конденсатора и боковой цилиндрической поверхности
Имеем уравнение,
|
|
(9.8) |
которое мы хотели бы проверить на непротиворечивость.
Интегрируем его по поверхности S1 (рис. 9.4). Получаем
|
|
(9.9) |
Из этого равенства обычно получают величину магнитного поля B для бесконечно длинного проводника. Напомним, что поверхность, по которой ведется интегрирование, может иметь любую форму, при условии, что она опирается на контур G. Воспользуемся этим и интегрируем это же уравнение (9.8) по поверхности S2. Получаем
|
|
(9.10) |
Здесь краевыми эффектами пренебреженно, Интеграл по боковой (цилиндрической) поверхности равен нулю, если выбрать радиус цилиндра достаточно большим. Выражения (9.9) и (9.10) противоречат друг другу. Значит, уравнение (9.8) неверно и его надо изменить. Простейший путь — добавить в правую часть уравнения (9.8) неизвестный вектор, который мы обозначим как 
|
|
(9.8а) |
Найдем неизвестный вектор , полагая, что он не равен нулю лишь между обкладками конденсатора. Для этого интегрируем отдельно по поверхностям S1 и S2 и приравниваем результаты. Интеграл по S1 вычислен в (9.9), а интеграл по S2 есть
Приравниваем:
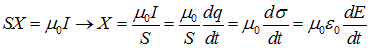
Итак,
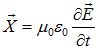
— вместе с (9.8a) получили уравнение Максвелла
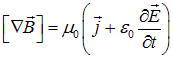
Максвелл назвал величину
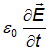
плотностью тока смещения:
|
|
(9.11) |
Так как численные значения плотности тока смещения jсм и плотности тока проводимости j равны, то, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между пластинами (обкладками конденсатора).
Если ввести понятие полного тока, который включает в себя сумму тока проводимости и тока смещения, то для его плотности имеем
|
|
(9.12) |
На примере конденсатора мы обнаружили, что полный ток будет замкнут: его линии продолжаются, нигде не прерываясь (даже в пространстве между пластинами конденсатора). По этому своему свойству именно полный ток должен стоять в правой части уравнения (рис. 9.5). В этом и состояла идея Максвелла.
Рис. 9.5. Лампочка, подключенная к сети переменного тока через конденсатор,
постоянно горит, так как ток проводимости внутри проводника переходит в ток смещения между пластинами конденсатора
В результате мы можем сформулировать (рис. 9.6)
Утверждение 4.
|
Вихревое магнитное поле создается полным током, то есть током проводимости и током смещения, вызванным изменяющимся электрическим полем. |
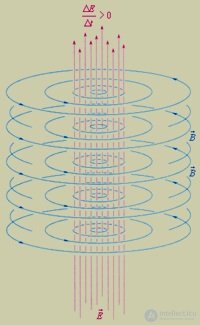
Рис. 9.6. Гипотеза Максвелла. Изменяющееся электрическое поле порождает вихревое магнитное поле
Математическим выражением этого утверждения является уравнение, получаемое из (9.11),
|
|
(9.13) |
Таким образом, Максвелл предсказал новое явление, в известном смысле обратное электромагнитной индукции. Эксперимент подтвердил, что магнитное поле действительно может создаваться изменяющимся во времени электрическим полем (рис. 9.7).
Рис. 9.7. Переменное электрическое поле между пластинами конденсатора порождает вихревое магнитное поле, которое измеряется с помощью проволочной квадратной рамки и отображается на экране монитора
В ряду этих экспериментов первым и главным было экспериментальное доказательство существования электромагнитных волн, выполненное немецким физиком Генрихом Герцем в 1888 году (рис. 9.8). Интересно, что сам Герц не верил в их существование и своими экспериментами хотел опровергнуть теорию Максвелла, созданную им за 20 лет до этого в 1865 году.
Рис. 9.8. Генрих Герц (1857 - 1894) - немецкий физик.
Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства — поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Ему удалось измерить на опыте длину волны и скорость распространения электромагнитных волн, которая оказалась равной скорости света (рис. 9.9).
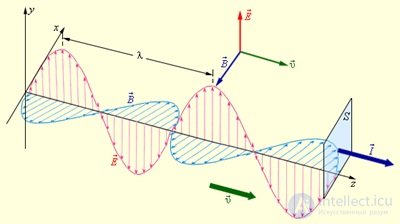
Рис. 9.9. Гармоническая электромагнитная волна, бегущая вдоль оси z . Вектора напряженности электрического поля, индукции магнитного поля и скорости волны взаимно перпендикулярны
Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи, продемонстрированной А.С. Поповым в 1895 г. (рис. 9.10).
Рис. 9.10. А.С. Попов (1859–1905) — русский физик и электротехник
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент p(t) которого быстро изменяется во времени. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ (рис. 9.11).
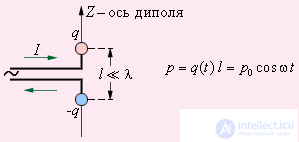
Рис. 9.11. Элементарный электрический диполь, совершающий гармонические колебания
Рис. 9.12 дает представление о структуре электромагнитной волны, излучаемой таким диполем.
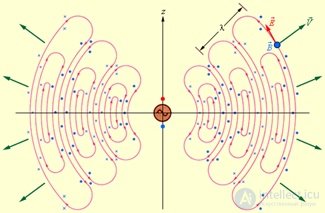
Рис. 9.12. Излучение элементарного электрического диполя. Дипольный момент направлен вдоль оси z, силовые линии электрического поля лежат в плоскости листа, а силовые линии магнитного поля перпендикулярны плоскости листа
Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.
Четыре уравнения, соответствующие нашим (модифицированным) утверждениям, называются уравнениями Максвелла в интегральной форме.
Выпишем их все рядом еще раз:
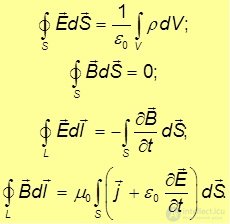
Чтобы получить уравнения Максвелла в среде, надо произвести замену:
,
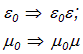то есть указать связь (так называемые «материальные» уравнения) между напряженностями и индукциям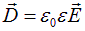и: 
и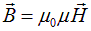 
и дополнить систему уравнением закона Ома
.
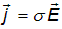Отметим, что приведенными выше простейшими соотношениями можно пользоваться не всегда. Ситуация заметно сложнее в присутствии таких веществ как сегнетоэлектрики, пьезоэлектрики, ферромагнетики, вещества анизотропные и тому подобное. Здесь наша цель показать, как формируется полная система уравнений, позволяющая (с учетом начальных и граничных условий, разумеется) рассчитать электромагнитное поле.
От уравнений в интегральной форме можно с помощью теорем векторного анализа перейти к уравнениям в дифференциальной форме, связывающим значения полей 
и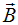 
и их пространственных и временных производных со значениями плотностей заряда и тока. Этими уравнениями мы пользоваться не будем, но все же приведем их хотя бы как часть шутки, опубликованной в одном из журналов в дни юбилея Максвелла:
«И сказал Бог:
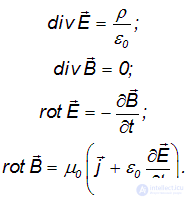
И стал свет».
Непонятные значки div (читается «дивергенция») и rot (читается «ротор») — это особые операции дифференцирования, выполняемые над векторными полями. Дивергенция — по латыни «расхождение». Эта операция описывает конфигурацию силовых линий типа «ежа», расходящихся из точек, где имеются электрические заряды. Слово «ротор» в переводе не нуждается, оно явно ассоциируется с вращением. Эта операция описывает вихревые поля (кольцеобразные — замкнутые силовые линии) вокруг их источников — токов или других полей, меняющихся во времени.
Четыре интегральных уравнения и четыре дифференциальных эквивалентны. Максвелл показал, что все явления электромагнетизма можно полностью описать этими четырьмя уравнениями, являющимися обобщением экспериментальных фактов.
В приведенной шутке упоминался свет. Действительно, свет — это электромагнитное излучение определенного диапазона частот. Предсказание электромагнитных волн стало одним из величайших достижений теории Максвелла. Представим себе, что заряды и токи отсутствуют. Посмотрим на уравнения Максвелла в дифференциальной форме. Видно, что если поля не статические, но зависят от времени, то имеется вихревое электрическое и магнитные поля (соответствующие роторы отличны от нуля). Распространение полей без зарядов и токов — это и есть электромагнитные волны. И можно углядеть в уравнениях намек на скорость их распространения: туда входит комбинация e0m0, через которую может быть выражена скорость света в вакууме (см. (6.3))
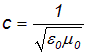
Но об этом — позже, в следующей части нашего курса.
В заключение же этой части процитируем слова Г. Герца об уравнениях Максвелла:
«Трудно избавиться от чувства, что эти математические формулы живут независимой жизнью и обладают своим собственным интеллектом, что они мудрее, чем мы сами, мудрее даже, чем их первооткрыватели, и что мы извлекаем из них больше, чем было заложено в них первоначально».
Пример использования уравнений Максвелла
Определить величину магнитного поля в зазоре конденсатора как функцию r расстояния от оси симметрии (рис. 9.13)
|
|
Рис. 9.13. Конденсатор с круглыми пластинами в процессе зарядки
Решение
Запишем уравнение (9.13) для контура, показанного на Рис. 9.3 штрихованной линией. Интегрируя, получим
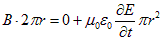
или
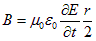
Очевидно, что магнитное поле не равно нулю только благодаря наличию меняющегося со временем электрического поля. В свою очередь, изменение электрического поля обусловлено увеличением заряда на обкладках конденсатора. Эту связь получим из соотношений
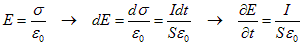
Окончательно находим
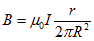
Согласно полученной формуле,
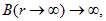
что явно неверно. В чем ошибка?
ОТВЕТ: формула справедлива только при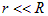 
.
Исследование, описанное в статье про уравнения максвелла, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое уравнения максвелла, вихревое электрическое поле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Переменный электрический ток. Электромагнитное поле
Комментарии
Оставить комментарий
Переменный электрический ток. Электромагнитное поле
Термины: Переменный электрический ток. Электромагнитное поле