Лекция
Привет, Вы узнаете о том , что такое колебания струн, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое колебания струн, колебания стержней, колебания воздушных столбов , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются все углы его отклонения относительно вертикали; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с превращением энергии из одной формы в другую и обратно.
Колебания различной физической природы имеют много общих закономерностей и тесно связаны c волнами. Поэтому исследованиями этих закономерностей занимается теория колебаний и волн. Принципиальное отличие волн в том, что их распространение сопровождается переносом энергии.
колебания струн , стержней и воздушных столбов являются объектом изучения в области физики, акустики и механики. В каждом случае, колебания происходят вокруг равновесного положения и характеризуются свойствами среды и граничными условиями.
Колебания струн:
Колебания стержней:
Колебания воздушных столбов:
Изучение колебаний струн, стержней и воздушных столбов позволяет понять основные законы волновой динамики, резонансные явления, акустические свойства и их применение в различных областях, таких как музыка, инженерия.
От анализа стоячей волны вообще переходим к анализу стоячих волн в конкретных ситуациях.
Начнем с колебаний струны колебания струн.
Колебания струны можно рассматривать как частный случай стоячих волн: на обоих закрепленных концах струны происходит отражение бегущей волны, приводящее к образованию стоячих волн (рис. 2.27). Эта устойчивая картина стоячих волн будет иметь место при закреплении любого конца струны в любом из узлов. Следовательно, на длине струны L между закреплениями может укладываться целое число т полуволн 'к/2

Этим колебаниям соответствуют длины волн


Рис. 2.27. Колебания струны
Частоты этих колебаний выражаются следующим образом:
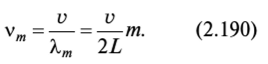
Колебания струны с наименьшей (основной) частотой vb при которой на струне укладывается одна пучность (т.е. полуволна Х/2), дает основной тон в звучании струны (рис. 2.27, вверху). Остальные колебания с кратными частотами соответствуют кратным частотам (обертонам) — см. рис. 2.27 сверху вниз.
Рассмотренные закономерности управляют не только колебаниями струны во многих музыкальных инструментах и образованием стоячих волн в них (скажем в резонаторе гитары), но проявляются также в модели излучения абсолютно черного тела, в квантовой механике, в физике твердого тела и др. Обо всем этом читатель узнает в соответствующих главах.
В конце прошлой статьи мы с вами видели что если на концах пружинки а струна фактически такая же по своим свойствам как пружинка просто значительно более упругая. Существует узлы то колебания могут происходить на строго определенных частотах эти частоты называются собственными частотами колебаний собственные частоты колебаний давайте на эти собственные частоты сейчас найдем мы с вами выяснили что струне на концах обязательно должны быть узлы а посередине могут быть несколько пуч настей 1 пуч ность то есть возможны несколько типов стоячих волн давайте изобразим первый из них струна имеют длину l келли и вот один из типов стоячей волны в такой струне это два узла на краях и 1 пучность посередине мы с вами уже выяснили что между узлами расстояния половина длины волны ранга пополам ниже оставьте себе место рисунок будет развиваться вниз значит в этой ситуации клей равняется линда пополам другой вид колебаний которые мы получили с вами на пружинке и можно получить на струне я вам продемонстрирую это чуть позже это когда посередине тоже есть узел и пучности 2 вот так длина струны по-прежнему эль но теперь здесь линда папиллом здесь ранга пополам то есть теперь длина струны равняется дважды лямда пополам а можно сделать так что на длине струны уложится не две-три пучности и два узла вот таким образом расстояние между узлами лямда пополам значит вот это линда пополам вот это линда попало и это тоже линда попал всего мы получили что на длине струны уложилась 3 полу волны вот так давайте напишем в общем случае что здесь может стоять единица двойка тройка или любое натуральное число то есть мы можем записать в общем случае в общем случае длина струны содержит в себе полуголого откуда длина волны струне равняется 2 3 деленное на но нам нужно найти частоты колебаний частота и длина волны связаны через скорость через скорость волны c равняется не умножить на линга следовательно мы можем написать c равняется не умножить на 2 делить на м подставляю сюда линда или не равняется c деленная на 2 л c деленная на 2 умножить на целое число m это число нумирует собственные частоты то есть чистота на которой может колебаться струна ни одна их множество и число m является номером этой частоты поэтому мы можем написать news индексом м вот эта формула где m 1 2 3 и так далее и дает нам набор собственных частот струны не надо эту формулу запоминать нужно просто помнить как оно выводится когда вы любую задачу решите сами легко собственные частоты струны струны между прочим то чем мы сейчас с вами занимаемся встретиться студентам когда они будут изучать квантовую механику оказывается в квантовой механике точно такие же задачи решаются здесь одна и та же природа недаром квантовую механику с одной из самых современных областей физики называют волновая механика так но мы отвлеклись и не первая называется основная частота первая гармоника или основной тон основная частота или основной тон или же ее называют первая гармоника частоты не u2 и u3 и так далее называют обертонами или кратными частотами кратная частоты обертоны или высшие гармоники высшие гармоники знакомое название знакомая терминология кратные частоты помните мы с вами изучали колебания кратных частот и мы выяснили так не м с изучали сложения колебаний кратных частот и мы выяснили что при сложение колебаний кратных частот результирующее колебание будет не гармоническим но периодическим процессом здесь давайте зададим себе вопрос в струне возможны вот такие колебания струне возможны вот такие колебания возможны такие а возможно ли одновременно существование всех таких типов колебания а почему нет возможно но результат сложения этих колебаний будет периодическим процессом период которого определяется основной частотой поэтому она так и называется основной тон а что же зависит от того сколько обертонов и какова их интенсивность давайте поэкспериментируем ножевой струне ну лучше всего экспериментировать с басовой струной сейчас мы возбудим стоячую волну в этой струне короче просто ее дернем сейчас в этой струне сосуществуют стоячие волны всех этих типов по-разному дергая струну мы можем возбуждать колебания отдельных составляющих с разной амплитудой как это будет выглядеть наверное мы не увидим но мы можем услышать слушайте [музыка] звук имеет одну и ту же высоту об этом подробнее мы завтра поговорим но у него разная окраска почему так потому что разные амплитуды вот этих вот собственных частот более того те кто знаком со струнными инструментами знают что можно возбуждать колебания в струне так что некоторые из этих собственных частот будут отсутствовать например сейчас я сделаю так чтобы не было вот этого а было только это не было вот этого а было только 4 и
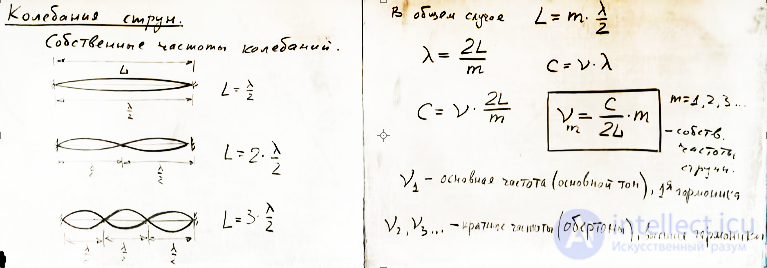
все четные гармоники для этого надо не дать колебаться серединке струны то есть там где кучность если приложить палец то колебания у которых кучность находится в этой точке a new за тухнут например возьмем коснемся середины струны и возбудим колебания сначала без прикасания такой звук а вот теперь split касанием ямале могу палец отпустить колебания все равно продолжаются я могу палец прижать струна при этом не тухнет колебания продолжаются потому что здесь узел сейчас в этой струне вот такие колебания существуют и колебания с 4 6 с четвертым шестым номером мы можем прижать струну вот здесь или здесь тогда колебания вот такие возможны атаки и такие уже будут невозможны потому что в этой точке здесь колебания пальцем заглушу и здесь а их заглушу вот эта точка струны значит смотрите струна длиннющая басовая струна звучит высоким тоном потому что погашены вот эти колебания такой способ звукоизвлечения знают все сотрудники называется флажолет . Об этом говорит сайт https://intellect.icu . Флажоле́т (старофр. flageolet «маленькая флейта») — прием игры на струнных смычковых и щипковых инструментах, заключающийся в извлечении звука-обертона. Флажолет и мы можем из такой вот басовой струны извлекать колебания разных частот ну тут уже тяжело причем обратите внимание вот эта нота ми только и это тоже меня не отличаются на октаву здесь есть возможность ноту ми извлечь на четвертой струне так можно настраивать гитару без всякого тюнера есть еще одна нота ми на гитаре на какой струне гитаристы на 1 я могу и этот он получить на басовой струне вот так значит как вы видите струна это богатейший объект и интересно с ней поиграться.
здесь очень много физики и музыки одновременно может поэтому физики часто очень любят музыку перейдем к колебаниям стержни и ладно сделаем вид что ничего не было эта гитара и не такое переживала посмотрите внимательно на ее корпус колебания стержни мы будем рассматривать стержня не продольные колебания хотя они тоже возможны поперечные колебания но деформация стержня или вот деформация пластины это изгибные волны поэтому много рассказать о стоячих волн их в стержнях мы не сможем поскольку теории изгибных волк сильно отличается от теории например колебаний струны это связано с тем что оказывается скорость изгибные волны зависит от чистоты это так называемая дисперсия но на качественном уровне кое с чем мы с вами познакомимся и так это не стержень но что-то вроде стержня давайте попробуем в этом стерни создать в этой пластине создать стоячую волну для этого нужно в узлах закрепить этот стержень потому что если закреплять его не в узлах то колебания погаснут и вот как это можно сделать допустим здесь и здесь мы позволим быть пучности посередине тоже кучность а посередине между точностями узел то есть на четверти и на трех четвертях длины этой пластины линейке мы закрепим ее просто положим на две резинки вот так и теперь мы можем заставить эту линейку колебаться вот стоячая волна изгиб на вате па в стержне на конце 2 пучности посередине пошлость и посередине два узла вот такой тип колебаний вот не деформированы стержень давайте даже пунктиром нарисуем его мы делим его пополам еще пополам и еще пополам и вот здесь на четверти и на трех четвертях длины располагаем крепление и тогда стоячая волна будет вот такой вот такая стоячая волна допустим это длина стержня тогда вот это расстояние расстояние между узлами это линда по пулям лямда пополам значит эльф равняются чему просто для мда здесь четвертушку здесь половинкой здесь четвертушку следовательно чистота не равняется скорость волны делить 0 на или часто таню равняется скорость волны делить на длину это частота вот такого типа колебания а что если мы попробуем узел в серединке создать чтобы по краям были две пучности вот не деформированы стержень попробуем создать вот здесь узел то есть закрепим здесь а на краях 2 пучности вот так тогда с одной стороны это будет длина стержня но с другой стороны это будет половина длины волны в этом стержни в этой колеблющиеся пластине лямда порталом отсюда у нас получается что лямда пополам равняется или или лямбда равняется 2 л или не равняется давайте обозначим у не штрих равняется чему с делить на 2 м то есть у нас получается если забыть о дисперсии считать что у нас одинаковая скорость волны любой длины любой частоты то получается что не у штрих равняется не пополам ну во всяком случае если даже есть дисперсия то есть если скорость звука изгибные волны зависит от частоты бог с ней во всяком случае не штрих меньшей не то есть такие колебания должны быть более низкочастотными чем такие на линейке мы этого проверять не будем мы возьмем трубу стержень труба безразлично давайте сейчас создадим колебания вот такого типа для этого я уже тут готовясь к уроку разметил эту трубу вот серединка трубы вот четвертушку вот три четверти вот так если закрепите сейчас ударить по трубе она начнет колебаться вот таким вот образом можно ее не держать за оба конца . Просто вот здесь укрепить я сейчас ударю по этой трубе и вне возникнут возникнуть стоячая волна с двумя сущностями на концах и еще прочность по серединке одержу я за узел возникает тихий звук поэтому тихонечко сидеть и вот я к микрофону поднесу вам может быть не слышно как это не годится хе-хе низкий звук не вот такой примерно теперь давайте попробуем ничего что вы его не слышите попробуем теперь взять страну за серединку мы ожидаем получить тон ну если не в два раза то по крайней мере ниже чем предыдущие тогда его вообще не должно быть слышно по крайней мере вам ну а зрители могут услышать очень низкий звук ударим по струне ничего подобного вместо этого мы слышим сразу два тона высокий и низкий один почти писк а второй такой звонки музыкальный звук а куда же девался вот этот вид колебаний оказывается он запрещен законами природы посмотрите ведь когда у нас происходит переход от вот этого состояния к этому то это точка движется вниз это точка движется вверх то есть в конечном счете стержень поворачивается при этом он обладает каким-то моментом импульса потом он разгоняется максимально этот момент импульса максимален потом он замедляется останавливается вот в этом положении

вы же не забыли что вокруг узла точки колеблются в противофазе то есть струн стержень должен колебаться вот так но извините для этого нужно прикладывать к нему какой-то момент силы чтобы изменялся момента импульса а он закреплен посередине поэтому никакой момент силы здесь не может возникнуть при таком закрепление стерни значит не может меняться момент импульса сам значит такой тип колебания запрещен законом сохранения момента импульса запрещен в квантовой механике существуют так называемые правила отбора которые запрещают в атомах колебания некоторых типов они тоже являются следствиями закона сохранения момента импульса мы сейчас занимаемся интереснейшими вещами которыми потом вы снова будете заниматься только уже изучая современную физику и так запрещен а что же в таком случае мы наблюдаем за звук давайте попробуем исследовать что это за два звука одновременно чтобы исследовать эти колебания надо поискать еще узлы смотрите здесь два звука а вот оказывается если я возьмусь за эту точку то останется один из звуков слушайте высокочастотный заглох а низкочастотный остался значит здесь еще узел вот узел вот узел я даже за этот узел могу держаться и низкий звук существует а высокий нет что это за колебание смотрим здесь узел здесь узел здесь кучность здесь кучность значит разрешенный вид колебаний имеет вот такую конфигурацию узел узел узел по серединке скрою скрою и вот вот такой вид имеет стер колебания стержня которые мы слышим узел узел узел это . например движется вверх а это точка движется вниз это точка движется вверх это точка движется вниз суммарный момент импульса как был 0 так и остается закон не нарушается вот разрешенный вид колебаний в стержне высокий тон тоже можно исследовать вот сейчас еще раз послушаем а баттона высокие где он вот еще узел один соответствующий вот этому высокому тону значит здесь узел здесь узел и наверно где-то здесь узел я уже не буду рисовать кучность узел кучность где-то здесь узел и кучность здесь и узел здесь поищем тут узел тут узел и посередине должен быть узел значит здесь где-то должен быть узел .
Факторами, ответственными за вибрацию воздушных столбов, являются:
Воздух внутри труб духового инструмента вибрирует. Трубка в духовом инструменте ограничивает движение воздуха внутри себя — частицы воздуха должны колебаться параллельно стенкам трубы. В результате в столбе воздуха внутри трубы возникает продольная стоячая волна. Концы, открытые или закрытые, создают узлы или пучности.
Музыкальные инструменты, такие как флейта, кларнет, натхасварам и т. д., известны как духовые инструменты. Они работают по принципу колебаний воздушных столбов. Простейшая форма духового инструмента – органная труба. Он состоит из деревянной или металлической трубы, которая производит музыкальный звук. Например, флейта, кларнет и натхасварам относятся к органным духовым инструментам.
я могу здесь взять и о звучании сохраняется ну надо точнее подобрать вот так так что колебание стержни тоже очень сложный процесс и любознательный физик может много для себя полезного узнать играясь просто с куском алюминиевой трубы колебания воздушных столбов да кстати физика тесно связана с музыкой какой музыкальный инструмент работает вот падает по этому принципу ксилофон ксилофон где источником звука служат вот такие пластинки и каждая пластинка обязательно закреплена вот таким образом ударяя молоточком по таким пластинкам мы вызываем изгибные колебания стоячие волны зависимости от длины пластинки длина волны будет разное соответственно будет разный и частота звука а значит и высота тона впрочем об этом завтра подробнее поговорим теперь колебания воздушных столбов сразу приходит в голову духовые инструменты колебания воздушных столбов но эти столбы колеблются они в открытом воздухе в трубах например в органных трубах и сейчас мы рассмотрим виды стоячих волн в органных трубах оказывается существует два вида органных труб закрытые трубы и открытые трубы они отличаются друг от друга только тем что в закрытой органной трубе с одной стороны донышко есть а с другой нет а в открытой оба конца свободны и так закрытая органная труба у нас нет органной трубы за ней взамен в нее мы будем пользоваться канализационном и так закрытая труба вот она с одного конца на заглушена с другого конца на открыто там где она заглушена колебания частиц воздуха невозможны мешает донышко а вот наверху колебания возможны воздух может входить и выходить значит здесь можно возбудить стоячую волну такую что здесь будет кучность дальше по мере продвижения вглубь трубы амплитуда этих колебаний будет убывать а здесь в точке где труба закрыта будет узел но показывать колебаний вот таким образом неудобно поэтому я просто в качестве иллюстрации буду показывать как бы поперечные колебания но на самом деле помним что они проданы вот конфигурация стоячей волны в закрытой органной трубе узел внизу кучность всегда там где открытый конец длина органной трубы или но и мы видим что на длине органной трубы в таком варианте стоячей волны на этой собственной частоте укладывается расстояние между узлом и кучностью мы выяснили что оно равно четверти длины волны значит здесь n равняется лямбда на 4 но можно в закрыт органы трубе создать и вот такой тип стоячей волны когда по-прежнему внизу будет узел но будет еще промежуточный узел вот так то есть здесь частицы будут колебаться здесь воздух неподвижен здесь частицы колеблются и внизу воздух неподвижен это у нас расстояние линда пополам лямда пополам а здесь от узла до пучности еще линда на 4 в результате получается что длина трубы состоит из лямда пополам плюс линда на 4 лямда на четыре плюс лямда пополам может быть и такой тип колебаний когда по серединке будет два узла вот здесь у нас получается лямда пополам здесь тоже лианга пополам это расстояние между узлами и здесь нам дано 4 тогда на длине органной трубы будет лямда на четыре плюс дважды линда пополам и или в общем случае у нас на длине трубы укладывается лямбда на четыре плюс эмма лямда пополам и отсюда можно найти возможной длины волны вот как в закрытой органной трубе и найти собственные частоты мы сейчас этого делать не будем нас будет интересовать только первая основная частота для нее 1 вот такая стоячая волна значит эль равняется лямда на 4 эльг равняется линда на 4 откуда лямбда равняется 4 л или если это мы хотим найти частоту то c равняется не u1 умножить на лямбда или c равняется ни один умножить на 4 л откуда ни один равняется c делить на 4п значит это основной тон закрытой органной трубы а теперь рассмотрим открытую органную трубу можно это стирать не ладно открытой органная труба она открыта с обеих сторон вот в таком случае точности будут и здесь и здесь х узел по серединке то есть здесь возможны колебания воздуха здесь возможны колебания х тут воздух стоит на месте не забудем что по 100 в
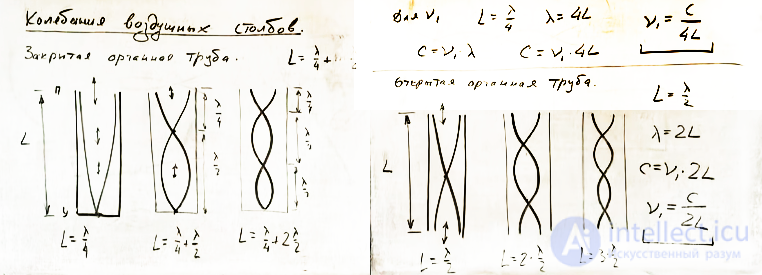
сторонах в противоположной стороны от узла колебания противофазу то есть когда здесь частицы воздуха движутся вниз тут они движутся вверх воздух сжимается разжимается сжимается разжимается картина стоячей волны вот такая пучности на концах узел посередине длина трубы и на длине трубы укладывается расстояние между двумя сущностями она тоже равняется половине длины волны l равняется линга пополам а возможно и более сложные колебания более высоких собственных частот покажем их здесь один узел но может быть и два узла вот такие колебания здесь у нас будет пол длинной волны плюс два раза четвертушку целая длина волны то есть цель равняется дважды линда пополам возможны такие колебания.
Здесь у нас два узла может быть и три узла [музыка] здесь у нас n равняется 1 раз лямда пополам два раза лямда пополам и еще третий раз лямда пополам 3 раза лямда пополам обратите внимание с этим набором отношений мы уже с вами встречались для струны точно такой же поэтому набор собственных частот открытой органной трубы точно такой же как набор собственных частот струны а здесь другое смотрите давайте найдем первую частоту основной тон открытой органной трубы для основного тона лямда пополам равняется r равняется линда пополам тогда линда равняется 2 или же c равняется ним 1 на 2 л или ним 1 равняется c делить на 2 л как для струн и сравните для закрытой органной трубы частота в два раза ниже чем для открытой органной трубы отношении частот в два раза музыканты называют интервалом в октаву значит закрытая органы труба должна звучать на октаву ниже чем открыты органы труба давайте проверим возьмем вот эту органную трубу и постучим по ней она резонирует на определенной частоте слышите высоту тона а теперь закроем и и с одного конца и послушаем раз никого там нет слышно на октаву ниже звук и как подойди сюда мне нужен человек у которого есть крепкая ладошка закрой трубу так плотненько слушаем открой закрой работает актом а уже то что мы сейчас с вами узнали говорит о том что можно использовать колебания воздушных столбов в музыкальных инструментах в органах причем в органах существуют как открытые такие закрытые органные трубы оказывается что набор собственных частот закрытой органной трубы относятся не как целые числа а как нечетные числа следующая гармоника будет уже в 3 раза больше по частоте чем 1 то есть четных гармоник там не будет в открытой органной трубе спектр.
Вспомним это слово такой же как и у струны и вот в органах используют и те и другие трубы и комбинируя их можно создавать очень богаты по тембру звуки можно эмулировать длину трубы меня я тогда частоту колебаний делается это в таких инструментах как тромбоны знаете там такая штуковина есть когда ее перемещаешь вверх в одну другую сторону то меняется высота тона в флейтах в саксофонах там есть отверстие закрывая и открываете отверстие вы можете менять длину трубы просто-напросто открывая ее в том или ином месте наконец существует музыкальный инструмент который называется флейта пана флейта пана вообще состоит из отдельных закрытых трубочек и их много каждая из этих трубочек настроена на свою длину волны а значит и на свою частоту вот я вчера сделал такую флейту вот это пробирка вовсе пустая а вот пробивка в которую на ли там много воды значит она видите издает более высокий тон здесь подобран ок некоторое количество пробирок с определенным количеством жидкости.
Вот музыкальный инструмент на котором можно играть пожалуйста в пику до нику понравилось да можете на перемене попробовать хотя нет вы наверное разольете ко мне еще математиком показывать было бы больше труб можно было бы продолжить эту мелодию так что как видите теория сухо но древо жизни зеленеет по-прежнему но и давайте в заключении решим одну задачку простенькая задачка просто повод для того чтобы познакомить вас с еще одним устройством задача номер 365 по задачнику гендри кого номер 365 бен греков расстояние между узлами стоячей волны создаваемой камертоном в воздухе 40 сантиметров определить частоту колебаний камертона скорость звука принять равной 340 метров в секунду расстояние между узлами стоячей волны создаваемой камертоном воздухе 40 сантиметров определить частоту колебаний камертона скорость звука ц 340 метров в секунду нужно найти частоту колебаний камертона нее что такое камертон камертон это устройство которое по английски называется tuning fork настроечная вилка вот эта вилка кстати самое первое вилки в истории состояли из двух зубьев они 3 или 4 как сейчас и мы можем ударяя молоточком поэтому камертону заставлять его звучать для чего этот ящик догадаться нетрудно это резонатор смотрите я не даю камертону звучать я буду просто постукивать по этому ящику слышите в его звучании прослушивается тот же тон на котором работает камертон то есть тут мы имеем дело с акустическим резонансом это резонатор колебания воздушного столба.
В этом ящике резонируют они настроены на ту же частоту что и колебания ножек камертона так вот этот камертон создает стоячую волну то есть вот тут находится камертон вот его резонаторный ящик из резонаторного ящика выходит волна она наверное там достигает стенки отражается и тут накладывается падающая и отраженная волна и вот тут стоячая волна и по условию задачи расстояния между узлами этой стоячей волны 40 сантиметров но тут будет узел так тут второй узел то есть вот какая-то вот такая тут стоячая волна в воздухе вот это расстояние l и по условию задачи равно 40 сантиметров но с другой стороны мы с вами знаем что расстояние между узлами стоячей волны это лямда пополам значит n равняется лямда пополам скорость звука нам дано вспоминая что скорость волны это произведение длины на частоту мы можем сейчас подставить сюда длину волны лямбда у нас отсюда равняется 2m так что c равняется 2 умножить на нем откуда частота колебаний камертона который создает у нас стоячую волну равняется c делить на 2 вот наша рабочая формула считаем не равняется c скорость звука 340 метров в секунду делить на два на 0,4 метра метры сократятся ответ будет в обратных секундах мы мы понимаем что если речь идет о чистоте нужно в конце написать hertz значит триста сорок сорок делим делим на ноль восемь получается как сказал кто дима до 425 425 обратных секунд но мы пишем birds на такой частоте колебался камертон все на

Анализ данных, представленных в статье про колебания струн, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое колебания струн, колебания стержней, колебания воздушных столбов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика