Лекция
Привет, Вы узнаете о том , что такое теплоемкость кристаллов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теплоемкость кристаллов, квантовая статистика , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
Мы завершаем свое знакомство со статистической физикой. Классическая статистика, математически выраженная распределением Максвелла — Больцмана, подсчитывала число частиц, находящихся в малом объеме 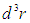 вокруг некой точки
вокруг некой точки 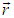 и имеющих импульсы в малом объеме
и имеющих импульсы в малом объеме 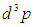 вокруг некоторой точки
вокруг некоторой точки  в пространстве импульсов. Познакомившись с законами квантовой механики, мы теперь понимаем, что для квантовых систем такой подход неприменим: микрочастицы не могут одновременно иметь определенные значения координаты и импульса, так что необходимо учесть соотношение неопределенностей Гейзенберга. Кроме того, мы уже знакомы с принципом Паули, согласно которому электроны «мешают» друг другу и не могут занять одно и то же состояние. Очевидно, что это также должно найти отражение в квантовой статистике, знакомству с которой посвящена настоящая глава. Первое и почти очевидное применение
квантовая статистика нашла в теории теплоемкости твердых тел. Мы коснемся также интереснейших макроскопических квантовых явлений — сверхтекучести и сверхпроводимости.
в пространстве импульсов. Познакомившись с законами квантовой механики, мы теперь понимаем, что для квантовых систем такой подход неприменим: микрочастицы не могут одновременно иметь определенные значения координаты и импульса, так что необходимо учесть соотношение неопределенностей Гейзенберга. Кроме того, мы уже знакомы с принципом Паули, согласно которому электроны «мешают» друг другу и не могут занять одно и то же состояние. Очевидно, что это также должно найти отражение в квантовой статистике, знакомству с которой посвящена настоящая глава. Первое и почти очевидное применение
квантовая статистика нашла в теории теплоемкости твердых тел. Мы коснемся также интереснейших макроскопических квантовых явлений — сверхтекучести и сверхпроводимости.
Простейшей моделью кристалла является геометрически правильно построенная кристаллическая решетка (рис. 7.1), в узлах которой помещаются атомы, которые считаются материальными точками.
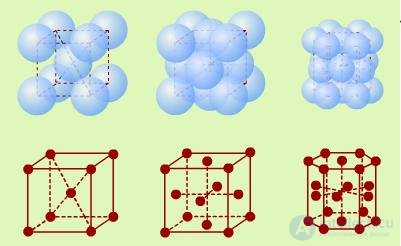
Рис. 7.1. Примеры кристаллических решеток
Видео 7.1. Некоторые кристаллографические и физические типы кристаллических решеток.
Атомы совершают тепловые колебания около положений равновесия. Если колебания малы, то их можно считать гармоническими. Энергия каждого атома складывается из кинетической и потенциальной энергий. На каждую степень свободы приходится в среднем кинетическая энергия
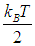
и такая же величина средней потенциальной энергии. Таким образом, среднее значение полной энергии, приходящейся на одну колебательную степень свободы, равно:
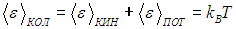
Напомним теперь классические результаты для теплоемкости кристаллической решетки, о которых говорилось ранее. Предположим для простоты, что все атомы одинаковы и каждый из них обладает тремя колебательными степенями свободы, а потому на него приходится средняя энергия 3kBT. Умножив эту величину на постоянную Авогадро NA, можно получить внутреннюю энергию одного моля кристаллического твердого тела:
|
|
|
(7.1) |
где R — универсальная газовая постоянная. Отсюда для молярной теплоемкости твердого тела имеем
|
|
|
(7.2) |
|
|
|
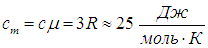
Если вещество кристалла состоит из молекул, имеющих nа атомов, то закон Дюлонга и Пти модифицируется очевидным образом:

(так, например, для молекул поваренной соли NaCl na = 2).
Недостатки классической теории теплоемкости
1. Классическая теория не дает объяснения зависимости теплоемкости тел от температуры. Экспериментально установлено, что при приближении к абсолютному нулю теплоемкости сV и ср всех тел, в том числе и кристаллов, стремятся к нулю.
2. По теореме о равномерном распределении энергии все степени свободы равноправны. Однако опыт приводит к заключению, что при низких температурах вклад в теплоемкость вносят не все из них: при понижении температуры определенные степени свободы становятся малоэффективными (говорят, что они «заморожены»). Так, при температуре

«замерзают» колебательные степени свободы (здесь 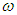 кол — частота осциллятора). Совершенно аналогично из-за квантования энергии вращения «замерзают» вращательные степени свободы: это происходит при
кол — частота осциллятора). Совершенно аналогично из-за квантования энергии вращения «замерзают» вращательные степени свободы: это происходит при

где I — момент инерции молекулы.
3. Закон Дюлонга и Пти был сформулирован для любого твердого тела: металла и диэлектрика. Однако металл состоит из положительно заряженных ионов, совершающих тепловые колебания вокруг узлов кристаллической решетки. Между ними движутся так называемые «свободные» электроны, которые ведут себя подобно электронному газу. Наличием свободных электронов объясняется высокая электрическая проводимость металлов. Классическая теория теплоемкости не принимает во внимание наличие электронного газа в металлах. Она учитывает только тепловые колебания ионов и приводит к результату Дюлонга и Пти. В отличие от диэлектриков, в металлах следовало бы учесть вклад в теплоемкость, вносимый электронами. На каждый свободный электрон приходится средняя кинетическая энергия

Поэтому по классической теории теплоемкость электронного газа должна быть сравнимой с теплоемкостью кристаллической решетки. Опыт показывает, что свободные электроны практически не вносят никакого вклада в теплоемкость металлов.
Квантовая теория устранила трудности, на которые натолкнулась классическая теория в вопросе теплоемкости твердых тел. Представим тело как систему N осцилляторов, не взаимодействующих друг с другом. Применим к этой системе закон распределения Больцмана, учитывая, что энергия гармонического осциллятора квантуется:
|
|
|
(7.3) |
Если обозначить Nn число осцилляторов с квантовым числом n, причем

то средняя энергия, приходящаяся на одну молекулу в состоянии термодинамического равновесия, определяется выражением
|
|
|
(7.4) |
Согласно распределению Больцмана, вероятность Рn найти осциллятор в состоянии с квантовым числом n равна
|
|
|
(7.5) |
Подставляя соотношения (7.5) и (7.3) для Рn и en в формулу (7.4) и выполняя суммирование, приходим к выражению для средней энергии гармонического осциллятора:
|
|
|
(7.6) |
Формула (7.6) отличается от полученного ранее выражения наличием дополнительного первого слагаемого.
Это слагаемое
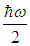
есть энергия «нулевых колебаний» гармонического осциллятора, которая не зависит от температуры и потому не вносит вклада в теплоемкость системы.
Выражение (7.6) было положено Эйнштейном в основу квантовой теории теплоемкости твердых тел. Эйнштейн представил кристаллическую решетку из N молекул как систему 3naN независимых гармонических осцилляторов с одинаковой собственной частотой  . Тогда внутренняя энергия одного моля определяется выражением
. Тогда внутренняя энергия одного моля определяется выражением

Дифференцируя его по температуре, получаем молярную теплоемкость кристаллической решетки твердых тел
|
|
|
(7.7) |
Это и есть формула Эйнштейна для теплоемкости кристаллов. При высоких температурах, когда

она переходит в классическую формулу
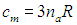
В другом предельном случае низких температур, когда

можно пренебречь единицей в знаменателе и получить
|
|
|
(7.8) |
При Т, стремящемся к 0, полученное выражение стремится к нулю, как это требует тепловая теорема Нернста (см. Поясним физический смысл этого результата. Из-за квантовой дискретности между основным и возбужденным уровнями системы осцилляторов имеется конечный энергетический зазор hw (энергетическая щель). Меньшее количество энергии осциллятор воспринять просто не в состоянии. При нулевой температуре в системе нет возбуждений — все осцилляторы находятся в основном состоянии. При небольшом повышении температуры тепловой энергии не хватает на преодоление этой щели, и лишь малое количество осцилляторов, пропорциональное
согласно закону Больцмана переходит на первый возбужденный уровень. Именно они ответственны за поглощение тепловой энергии и, соответственно, за малую теплоемкость кристалла при низких температурах. При высоких температурах тепловой энергии хватает на возбуждение многих вышележащих колебательных уровней, так что дискретность энергии уже не играет особой роли — мы возвращаемся к классическому результату Дюлонга и Пти.
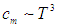

Рис. 7.2. Петер Йозеф Вильгельм Дебай
П. Дебай (рис. 7.2) учел, что колебания атомов в кристаллической решетке не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных между собой атомов, обладающих 3N степенями свободы. Каждая степень свободы (нормальное колебание) может быть представлена как гармонический осциллятор, среднюю энергию которого 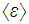 мы уже вычислили (см. (7.6)). Из-за связи между атомами частоты нормальных колебаний уже не совпадают между собой. Взаимодействие атомов приводит к тому, что колебание, возникшее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Эта волна, дойдя до границы кристалла, отражается. При наложении прямой и отраженной волн образуется стоячая волна, которой соответствует нормальное колебание кристаллической решетки. Число dN нормальных колебаний, то есть стоячих волн, в интервале частот от
мы уже вычислили (см. (7.6)). Из-за связи между атомами частоты нормальных колебаний уже не совпадают между собой. Взаимодействие атомов приводит к тому, что колебание, возникшее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Эта волна, дойдя до границы кристалла, отражается. При наложении прямой и отраженной волн образуется стоячая волна, которой соответствует нормальное колебание кристаллической решетки. Число dN нормальных колебаний, то есть стоячих волн, в интервале частот от  до
до  + d
+ d велико, поэтому суммирование в выражении для внутренней энергии системы может быть заменено интегрированием:
велико, поэтому суммирование в выражении для внутренней энергии системы может быть заменено интегрированием:
|
|
|
(7.9) |
Число колебаний в единице объема. В этом разделе мы займемся подсчетом числа стоячих волн, имеющих близкие частоты  . В сущности, мы проделали уже эти выкладки ранее для электромагнитного излучения, но повторим их снова с небольшими модификациями для применения также и к упругим колебаниям в кристалле.
. В сущности, мы проделали уже эти выкладки ранее для электромагнитного излучения, но повторим их снова с небольшими модификациями для применения также и к упругим колебаниям в кристалле.
Рассмотрим сначала одномерный потенциальный ящик длиной 1х. Мы могли уже убедиться, что стоячая волна в нем (неважно, электромагнитная ли, звуковая или волна де Бройля), описывается функцией sin (kx), которая должна обращаться в нуль на границах ящика. Отсюда
|
|
|
(7.10) |
Число nх нумерует различные стоячие волны вдоль оси х, и потому на малый интервал волнового вектора dkх приходится число колебаний
|
|
|
(7.11) |
Двойку в знаменателе мы поставили, чтобы избежать двойного счета: замена kх на –kх приводит к той же стоячей волне. В трехмерном ящике для волн, распространяющихся по другим осям, получаем аналогичные формулы
|
|
|
(7.12) |
Перемножая (7.11) и (7.12), находим для полного числа стоячих волн в ящике объемом V = lxlylz
|
|
|
(7.13) |
Наконец, учтем, что каждой стоячей волне может соответствовать g поляризаций (для волн де Бройля, соответствующих частицам со спином s, имеем g = 2s + 1 — число различных проекций спина). Окончательно имеем
|
|
|
(7.14) |
Формула (7.14) дает число различных стоячих волн (отличающихся числом узлов и направлениями поляризации) в объеме V, приходящихся на элемент объема d3k в пространстве волнового вектора. Далее, для перехода к частотам волн используем соотношение, полученное при изучении волновых процессов:

где v ≡ v — фазовая скорость волны. Отсюда
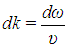
и окончательно получаем
|
|
|
(7.15) |
Мы вывели формулу (7.15) для прямоугольного объема, но можно показать, что форма объема не влияет на результат. Не имеет большого значения и физическая природа колебаний, число которых мы подсчитали. Например, для фотонов v = с и g = 2 (свет может иметь правую и левую циркулярные поляризации). В итоге получаем уже известную нам формулу для числа типов фотонов в объеме V в интервале частот d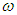 :
:
|
|
|
(7.16) |
Для применения (7.15) к звуковым волнам в кристалле учтем, что там возможна одна продольная волна, распространяющаяся со скоростью v||, и две поперечные волны с разными поляризациями, как у фотонов, распространяющиеся со скоростью v|. Очевидно теперь, как обобщить формулу (7.15) на данный случай:
|
|
|
(7.17) |
Здесь мы ввели величину v, играющую роль некого среднего между скоростями продольных и поперечных волн; она вычисляется из соотношения
|
|
|
(7.18) |
Характеристическая температура Дебая. Подставляя (7.17) и (7.6) в выражение (7.9) для внутренней энергии, получаем
|
|
|
(7.19) |
где 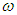 MAX — максимальная частота нормальных колебаний, которая определяется из соотношения
MAX — максимальная частота нормальных колебаний, которая определяется из соотношения
|
|
|
(7.20) |
так как полное число нормальных колебаний равно числу степеней свободы. Используя (7.17), находим
|
|
|
(7.21) |
где n — концентрация атомов (их число в единице объема кристалла). Таким образом, максимальная частота нормальных колебаний, называемая дебаевской частотой, равна
|
|
|
(7.22) |
Следует отметить, что наименьшая длина упругой волны в кристалле, которая соответствует максимальной частоте 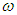 MАХ, равна
MАХ, равна
|
|
|
(7.23) |
где

— расстояние между соседними атомами в кристаллической решетке. Этот результат согласуется с тем, что волны, длины которых меньше удвоенного межатомного расстояния, не могут существовать в кристалле.
Используя определение (7.22) и учитывая, что для одного моля кристалла концентрация атомов равна
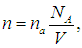
где nа — число атомов в молекуле вещества кристалла, мы можем записать внутреннюю энергию одного моля в виде
|
|
|
(7.24) |
Дифференцируя внутреннюю энергию U по температуре, можно получить молярную теплоемкость кристалла:
|
|
|
(7.25) |
Введем новый параметр — характеристическую температуру Дебая
|
|
|
(7.26) |
и выполним в интеграле (7.25) замену переменных

Тогда молярную теплоемкость кристалла можно записать в виде
|
|
|
(7.27) |
При низких температурах Т <<  D верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Об этом говорит сайт https://intellect.icu . Тогда интеграл будет представлять собой число
D верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Об этом говорит сайт https://intellect.icu . Тогда интеграл будет представлять собой число

и теплоемкость окажется пропорциональной кубу температуры:
|
|
|
(7.28) |
Эта приближенная зависимость известна как закон Дебая и хорошо согласуется с экспериментом при достаточно низких температурах Т <<  D.
D.
При высоких температурах Т >>  D экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора:
D экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора:
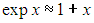
Тогда для молярной теплоемкости получается значение
|
|
|
(7.29) |
то есть закон Дюлонга и Пти.
О согласии теории Дебая с опытом можно судить по графику рис. 7.3, на котором показаны экспериментальные точки для некоторых веществ.
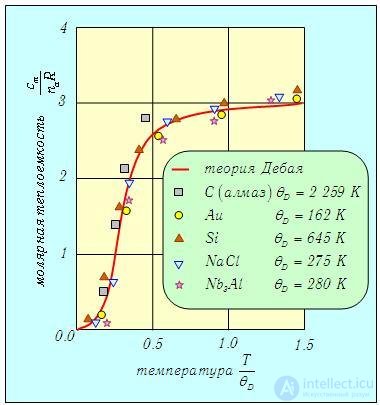
Рис. 7.3. Сравнение теории теплоемкости Дебая с экспериментальными данными: показаны вещества с заметно различающимися значениями дебаевской температуры и разным составом молекул (nа = 2 для NaCl и nа = 4 для Nb3Al), но все точки лежат достаточно близко от теоретической кривой
Пример. Пользуясь данными, приведенными на графике рис. 7.1, найдем максимальную частоту колебаний  MАХ в кристалле золота по теории Дебая.
MАХ в кристалле золота по теории Дебая.
Температура Дебая для золота, как указано на графике, равна  D = 162 К. Используя (7.26), находим
D = 162 К. Используя (7.26), находим

Как и внутри молекул, атомы в кристалле совершают малые колебания около фиксированных положений равновесия. Колебания атомов распространяются по кристаллу в виде слабо взаимодействующих волн с волновыми векторами k и частотами  (k). Физически нормальные колебания в кристаллах порождают волны деформации кристаллической решетки (то есть упругие волны). Таким образом, движение атомов в кристалле может быть описано как суперпозиция плоских волн различной частоты
(k). Физически нормальные колебания в кристаллах порождают волны деформации кристаллической решетки (то есть упругие волны). Таким образом, движение атомов в кристалле может быть описано как суперпозиция плоских волн различной частоты
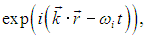
каждой из которых соответствует гармонический осциллятор с частотой  (k).
(k).
Следуя идеям де Бройля, такой упругой волне в кристалле можно сопоставить квазичастицу с энергией

и импульсом
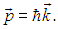
Она носит название фонона.
|
Фонон — элементарная порция звуковой энергии, подобно тому как фотон — элементарная порция световой (электромагнитной) энергии. |
Наше сопоставление можно схематически изобразить следующим образом (рис. 7.4):

Рис. 7.4. Схема «волна — частица»
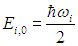
Индекс i стоит для обозначения типа соответствующей волны (продольная, поперечная, характеризующаяся определенным законом дисперсии
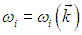
и т. п.), или, как говорят, фононной моды. При квантово-механическом рассмотрении гармонический осциллятор данной фононной моды, как мы уже знаем, может иметь энергию

При ni = 0 мы имеем нулевые колебания с энергией
— фонона данной моды в твердом теле нет. При ni = 1 мы имеем новое состояние с энергией возбуждения
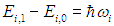
— это и есть квазичастица фонон. При произвольном квантовом числе ni энергия возбуждения равна

В таком случае мы говорим, что в твердом теле распространяются пi фононов данной моды i.
Используя полученные выше результаты, в случае термодинамического (теплового) равновесия можно найти среднее число фононов i> с частотой wi. Действительно, мы уже нашли среднюю энергию квантового осциллятора (см. (7.6), где частоту w надо заменить теперь на частоту упругой волны wi). С другой стороны, эту же энергию можно представить в виде (7.6)

Приравнивая эти выражения, получаем
|
|
|
(7.30) |
При низких температурах
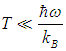
среднее число фононов экспоненциально убывает при T, стремящемся к 0: в системе не возникает возбуждений. Наоборот, при высоких температурах
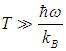
экспоненту в знаменателе можно разложить в ряд Тейлора и получить результат
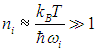
Следовательно, из полученного соотношения вытекает, что при достаточно высокой температуре в кристалле может одновременно возбуждаться неограниченное количество одинаковых фононов, то есть принцип Паули на фононы не распространяется. Напомним, что кванты электромагнитного поля — фотоны, находящиеся в состоянии равновесия со стенками полости, также подчиняются этому распределению.
Представление о фононах широко используется в физике твердого тела. Фононы называют квазичастицами, поскольку они хотя и вполне реальны, но существуют только в кристаллах: вне среды их нет. Идея существования квазичастиц была впервые выдвинута Л.Д. Ландау в 40-х годах прошлого века.

Рис. 7.5. Лев Давидович Ландау
Кроме фононов есть и другие типы квазичастиц. Тепловые колебания решетки можно рассматривать как фононный газ, при низких температурах — идеальный. При очень высоких температурах решетка плавится и модель невзаимодействующих фононов неприменима: они перестают быть свободными. Преимущество представления о фононах состоит в том, что в его рамках свойства твердого тела рассматриваются как свойства ансамбля большого числа независимых квазичастиц — идеального фононного газа. Все представления этой модели могут быть использованы для описания поведения кристаллической решетки.
Можно рассматривать также взаимодействие обычных частиц (электронов, фотонов) с фононами. Так, электроны, обмениваясь фононами, испытывают притяжение. Несмотря на кулоновское отталкивание, может даже образоваться связанное состояние пары электронов. Подобный механизм ведет к явлению сверхпроводимости (будет рассмотрено далее).
Мы уже убедились, что число фононов в твердом теле не постоянно. Фононов тем больше, чем интенсивнее тепловое движение атомов, то есть чем выше температура. C приближением к абсолютному нулю, их число стремится к нулю.
Две частицы тождественны, если все их физические свойства в точности совпадают, что исключает возможность экспериментально различать их. В классической теории всегда предполагается, что мы можем в принципе проследить за движением частиц и сказать, какая из них куда полетела. Поэтому в классической теории даже тождественные частицы в принципе различимы. В квантовой механике это не так: принцип неопределенности не позволяет прослеживать траектории и, стало быть, неразличимость частиц имеет принципиальный характер и влияет на результат вычислений.
Пусть, например, система из двух частиц описывается гамильтонианом (оператором энергии)
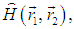
и пусть система находится в состоянии с волновой функцией
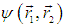
Введем оператор
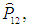
переставляющий частицы местами, то есть обменивающий их радиусы-векторы:
|
|
|
(7.31) |
Математически тождественность частиц выражается в инвариантности (неизменности) гамильтониана относительно операции перестановки
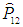
этих частиц, что в квантовой механике записывается как условие коммутации операторов
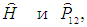
то есть
|
|
|
(7.32) |
Это условие обеспечивает физическую неразличимость частиц, поскольку тогда волновая функция  будет также решением уравнения Шредингера с тем же значением энергии. Действительно, если
будет также решением уравнения Шредингера с тем же значением энергии. Действительно, если

и мы подействуем на обе части этого уравнения оператором коммутации

то получим
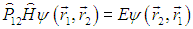
Из-за условия коммутации мы можем пронести оператор коммутации через гамильтониан:

и наше уравнение примет вид
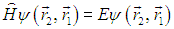
Но мы помним, что коммутирование операторов с гамильтонианом означает сохранение их собственных значений. Найдем собственные значения р оператора коммутации. Для этого надо решить уравнение
|
|
|
(7.33) |
С учетом определения (7.31) оператора коммутации, записываем это уравнение в виде
|
|
|
(7.34) |
Снова подействуем на обе части (7.34) оператором перестановки частиц:
|
|
|
(7.35) |
Из (7.34) и (7.35) получаем, что
|
|
|
(7.36) |
то есть р = +1. Таким образом, оператор коммутации может иметь только два собственных значения. При р = 1 волновая функция симметрична относительно операции перестановки частиц:
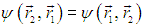
При р = –1 имеем антисимметричную волновую функцию:
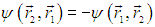
Таким образом, мы получили важный результат:
|
Волновые функции системы двух тождественных частиц могут быть либо четными, либо нечетными относительно операции перестановки частиц местами. |
Справедливо обобщение этого результата:
|
Состояния системы тождественных частиц либо симметричны, либо антисимметричны относительно перестановки любых двух из них. |
Какое состояние реализуется — зависит от природы рассматриваемых частиц.
|
Частицы с симметричными состояниями называются бозонами, с антисимметричными — фермионами. |
Ранее этими именами мы называли частицы с целым и полуцелым спинами, соответственно. В релятивистском уравнении Дирака, в отличиe от уравнения Шредингера, спин частиц возникает автоматически. Существует фундаментальная теорема Паули:
|
Частицы с полуцелым спином (s = 1/2, 3/2 и т. д.) описываются антисимметричными волновыми функциями, а с целым (s = 0, 1, 2 и т. д.) — симметричными. |
Эта теорема о связи спина со статистикой является следствием объединения квантовой механики с теорией относительности.
Обратимся для примера к состоянию двух атомных электронов. В пренебрежении взаимодействием между ними волновая функция распадается на произведение волновых функций каждого электрона по отдельности:
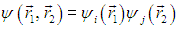
Индексы i, j обозначают здесь полный набор квантовых чисел (n, l, т, s), которыми одно состояние отличается от другого. Меняя электроны местами, приходим к состоянию с той же энергией, описываемому волновой функцией

Поэтому в силу принципа суперпозиции возможны состояния, описываемые любой линейной комбинацией этих двух функций, причем все они будут иметь ту же энергию. Однако мы теперь знаем, что для электронов со спином s = 1/2 физический смысл имеет лишь антисимметричная комбинация
|
|
|
(7.37) |
Если состояния электронов одинаковы (i = j, то есть совпадают все квантовые числа), то
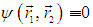
Мы снова пришли к принципу Паули:
|
Не может быть двух электронов в одном состоянии. |
Бозоны и фермионы имеют совершенно разные статистические свойства, то есть по-разному ведут себя в коллективе себе подобных. Кроме непосредственного силового взаимодействия между частицами, имеется специфически квантовое, обменное взаимодействие: это не какие-то дополнительные силы или поля — одни частицы влияют на поведение других одним своим присутствием. Эти эффекты ощущаются частицами, если они находятся друг от друга на расстояниях, меньших или порядка длины волны де Бройля  В. При высоких температурах энергии частиц велики и
В. При высоких температурах энергии частиц велики и  В мало — это область классической физики. При низких температурах
В мало — это область классической физики. При низких температурах  В возрастает и квантовые эффекты доминируют.
В возрастает и квантовые эффекты доминируют.
Рассмотрим систему одинаковых фермионов с энергиями Ei в состоянии i (где i обозначает набор квантовых чисел, включая спин). Обозначим через ni число частиц в состоянии i. Основной принцип статистической физики (классической и квантовой) формулируется исследующим образом:
|
Вероятность обнаружить систему в состояния i равна
|
Здесь С — нормировочная постоянная, а 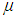 — химический потенциал. Этот параметр появляется всегда при фиксированном числе частиц в системе, которое равно
— химический потенциал. Этот параметр появляется всегда при фиксированном числе частиц в системе, которое равно

где сумма берется по всем состояниям. По сути дела, уравнение (7.38) — это обобщение известного распределения Больцмана. Из принципа Паули следует, что ni могут принимать лишь значения 0 и 1 — в данном состоянии i может быть либо одна частица, либо ни одной вообще.
Из всего набора возможных состояний системы проследим за каким-то конкретным состоянием k с энергией Еk. С некой вероятностью
|
|
|
(7.39) |
в нем может не оказаться ни одной частицы (пk = 0). С вероятностью
|
|
|
(7.40) |
в нем окажется одна частица (пk = 1). При записи формул (7.39), (7.40) мы использовали общее выражение (7.38) для вероятности
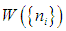 .
.
Поскольку третьего не дано, должно выполняться условие сохранения полной вероятности
 .
.
откуда следует
|
|
|
(7.41) |
Значит, среднее число частиц

в состоянии k получается равным
|
|
|
(7.42) |
Формула (7.42) является основой квантовой статистики Ферми — Дирака (рис. 7.6). При высоких температурах получаем
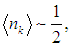
то есть равномерное распределение частиц по состояниям. Если число частиц N в системе фиксировано, то химический потенциал m определится из условия
|
|
|
(7.43) |
Подчеркнем также, что согласно (7.42) среднее число частиц в данном состоянии всегда не превышает единицы. Это — прямое следствие принципа Паули.

Рис. 7.6. Квантовая статистика Ферми — Дирака
Рассмотрим теперь систему тождественных бозонов. В этом случае число ni частиц в состоянии i может принимать любое значение от 0 до ,бесконечности (или от 0 до N при фиксированном числе частиц). Рассмотрим какое-то конкретное состояние k системы с энергией Еk. Тогда для вероятности, что в этом состоянии окажутся n частиц, получаем из основного соотношения (7.38)
|
|
|
(7.44) |
где
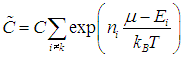
Сумма W(n) по всем значениям n (включая и нулевое) равна вероятности того, что в состоянии k окажется какое-то количество частиц или не окажется ни одной. Очевидно, такая сумма должна быть равна единице:
|
|
|
(7.45) |
Здесь мы использовали формулу
|
|
|
(7.46) |
для суммы бесконечно убывающей геометрической прогрессии при
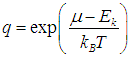
Теперь легко найти нормировочную постоянную:
|
|
|
(7.47) |
и полное выражение для вероятности W(n). Нас интересует в первую очередь среднее число частиц в состоянии k, которое по смыслу вероятностей выражается как

Сумму ряда вида

нетрудно вычислить дифференцированием по q выражения (7.46):
|
|
|
(7.48) |
Левая часть (7.48) может быть записана в виде
|
|
|
(7.49) |
Вместе с (7.48) это приводит к результату:
|
|
|
(7.50) |
Подставляя
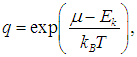
находим
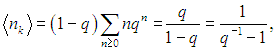
откуда следует основное соотношение квантовой статистики Бозе — Эйнштейна (рис. 7.7):
|
|
|
(7.51) |
Разница по сравнению с соответствующей формулой (7.42) для фермионов имеется только в знаке перед единицей в знаменателе. Из-за этого нельзя теперь утверждать, что среднее число частиц в данном состоянии всегда меньше единицы: принцип Паули не распространяется на бозоны. По физическому смыслу все nk > 0, следовательно,  < Е0, где Е0 — минимальная энергия системы (то есть энергия основного уровня). Для свободных частиц величина Е0 равна нулю. Отсюда следует, что для свободных бозонов химический потенциал отрицателен. По-прежнему имеется уравнение связи
< Е0, где Е0 — минимальная энергия системы (то есть энергия основного уровня). Для свободных частиц величина Е0 равна нулю. Отсюда следует, что для свободных бозонов химический потенциал отрицателен. По-прежнему имеется уравнение связи 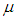 и N в случае фиксированного числа частиц:
и N в случае фиксированного числа частиц:
|
|
|
(7.52) |
При высоких температурах
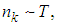
то есть с ростом температуры число бозонов в каждом состоянии растет.
Если в системе число частиц не фиксировано, а определяется условиями равновесия (например, равновесие излучения с веществом, когда фотоны поглощаются и испускаются), то 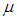 = 0. Применяя (7.51) к системе фотонов и учитывая, что для фотонов
= 0. Применяя (7.51) к системе фотонов и учитывая, что для фотонов

приходим к формуле (7.15) и ее аналогу для фононов (7.30).
Заметим, что при
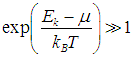
обе формулы (7.42) и (7.51) переходят в классическое распределение Больцмана. В этом случае

что можно интерпретировать как условие малой плотности частиц, то есть как квантовый аналог разреженного газа: в каждом квантовом состоянии фактически находится не более одной частицы. Значит, не существенно не только прямое взаимодействие частиц, но и их квантовое влияние друг на друга, обменные эффекты.
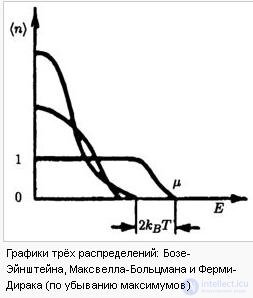
Рис. 7.7. Квантовая статистика Бозе — Эйнштейна
Не следует думать, будто законы квантовой механики важны только при рассмотрении явлений в масштабах атомов и молекул. При низких температурах вблизи абсолютного нуля существуют и макроскопические проявления этих законов. С ними мы и познакомимся в этом разделе.
Бозе — Эйнштейновская конденсация. Рассмотрим идеальный газ свободных бозонов, которые не взаимодействуют ни друг с другом, ни с внешним полем. Состояние частицы задается ее импульсом р и проекцией спина (имеется всего g = 2s + 1 возможностей, для бозонов s — целое число). Среднее число бозонов в данном состоянии к описывается формулой (7.51). Поскольку принцип запрета Паули на бозоны не распространяется, они могут накапливаться в одном состоянии. При нулевой температуре все частицы системы должны занять нижний энергетический уровень с Е = 0. Возникает вопрос, что будет при Т > 0 ?
Снова вспомним формулу (7.14) для числа типов колебаний, но заменим в ней волновой вектор на импульс частицы:

Получаем тогда
|
|
|
(1) |
Индексом «сост» мы хотим подчеркнуть, что, имея дело с квантовыми частицами, мы стали называть вещи своими именами: число колебаний становится в этом случае числом состояний, в которых можно обнаружить частицу. Элемент объема пространства импульсов можно записать в виде

где 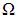 — телесный угол. Интегрируя соотношение (1) по углам, получаем число состояний dNp, в которых модуль импульса частицы заключен между значениями р и р + dp:
— телесный угол. Интегрируя соотношение (1) по углам, получаем число состояний dNp, в которых модуль импульса частицы заключен между значениями р и р + dp:
|
|
|
(2) |
Учитывая, что энергия свободной нерелятивистской частицы

так что
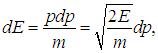
находим из (1) число состояний dNE с энергиями между E и E + dE:
|
|
|
(3) |
Умножая (3) на среднее число частиц в одном состоянии, находим число частиц, приходящееся на тот же интервал энергий:
|
|
|
(4) |
Чтобы получить полное число частиц в системе, проинтегрируем (4) по всем значениям энергии:
|
|
|
(5) |
Вводя новую переменную интегрирования

переписываем (5) в виде
|
|
|
(6) |
Это уравнение для химического потенциала 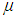 . В сущности, мы переписали формулу (7.52) в виде, удобном для практического применения: суммирование по всем возможным состояниям заменено на суммирование (интеграл) по энергии частицы, а число состояний учтено у нас при использовании формулы (3).
. В сущности, мы переписали формулу (7.52) в виде, удобном для практического применения: суммирование по всем возможным состояниям заменено на суммирование (интеграл) по энергии частицы, а число состояний учтено у нас при использовании формулы (3).
Если при заданной концентрации частиц N/V понижать температуру газа, то химический потенциал будет увеличиваться (то есть уменьшаться по модулю), как следует из (6). Предельного значения 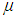 = 0 он достигнет при температуре Т0, определяемой уравнением
= 0 он достигнет при температуре Т0, определяемой уравнением
|
|
|
(7) |
откуда следует выражение
|
|
|
(8) |
Разберемся в физическом смысле входящих в формулу (8) комбинаций параметров. Если обозначить через l среднее расстояние между частицами, то в объеме сферы радиусом l/2 будет содержаться одна частица, то есть плотность частиц будет
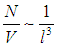 .
.
Поэтому формулу (8) можно переписать в виде
 .
.
Поскольку тепловая энергия движения частиц
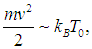
мы получаем отсюда
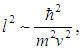
или

где  В — длина волны де Бройля (мы опустили в этом рассуждении несущественные числовые множители). Таким образом, снова приходим к выводу, что квантовые эффекты становятся заметными, когда длина волны де Бройля имеет порядок расстояния между частицами. Формула (8) — это общее выражение для «квантовой» температуры: оно еще нам встретится, а меняться может лишь числовой множитель.
В — длина волны де Бройля (мы опустили в этом рассуждении несущественные числовые множители). Таким образом, снова приходим к выводу, что квантовые эффекты становятся заметными, когда длина волны де Бройля имеет порядок расстояния между частицами. Формула (8) — это общее выражение для «квантовой» температуры: оно еще нам встретится, а меняться может лишь числовой множитель.
Итак, при Т > Т0 существует физически приемлемое (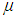 < 0) решение уравнения (6). При Т < Т0 химический потенциал остается равным предельному значению 0, дальше ему меняться некуда, и правая часть уравнения становится меньше N/V. Этот результат удивителен, ибо число частиц в системе фиксировано, и плотность частиц, казалось бы, должна оставаться неизменной. Стало быть, какая-то доля этих частиц куда-то девается, выпадает из системы, перестает участвовать в тепловом движении. Значит, правая часть (6) будет при Т < Т0 (
< 0) решение уравнения (6). При Т < Т0 химический потенциал остается равным предельному значению 0, дальше ему меняться некуда, и правая часть уравнения становится меньше N/V. Этот результат удивителен, ибо число частиц в системе фиксировано, и плотность частиц, казалось бы, должна оставаться неизменной. Стало быть, какая-то доля этих частиц куда-то девается, выпадает из системы, перестает участвовать в тепловом движении. Значит, правая часть (6) будет при Т < Т0 (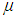 = 0) описывать те частицы, которые в тепловом движении участвуют, то есть энергия которых больше нуля:
= 0) описывать те частицы, которые в тепловом движении участвуют, то есть энергия которых больше нуля:
|
|
|
(9) |
Если умножить и разделить правую часть (9) на

то можно выделить фактор

а оставшийся сомножитель, в соответствии с (7), будет равен полному числу N частиц в системе:
|
|
|
(10) |
Остальные частицы имеют нулевую энергию; их число NE=0 определится как разность N – NE=0:
|
|
|
(11) |
Итак, при температуре ниже критической Т < Т0 происходит так называемая бозе — эйнштейновская конденсация — накопление частиц в состоянии с р = 0. Эффект этот — макроскопический, так как число частиц конденсата огромно, порядка полного числа частиц N. При понижении температуры ниже критической конденсат появляется внезапно — система испытывает резкое изменение свойств (как говорят, происходит фазовый переход).
При абсолютном нуле температуры все частицы системы находятся в конденсате. При повышении температуры некоторые из них покидают конденсат и начинают участвовать в тепловом движении. При Т > Т0 бозе-эйнштейновский конденсат исчезает: в нем не остается частиц. Зависимость доли частиц в конденсате от температуры показана на рис. 7.8.
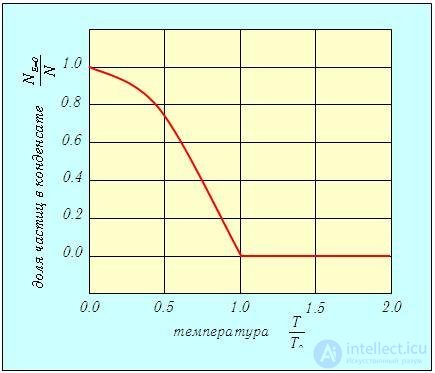
Рис. 7.8 Доля частиц в бозе-эйнштейновском конденсате в зависимости от температуры
Важно отметить, что конденсация происходит не в обычном пространстве, как при выпадении, например, росы, но в пространстве импульсов. С точки зрения нашего обычного пространства и конденсат, и нормальный компонент бозе-газа «размешаны», и система остается пространственно однородной. Но есть и сходство с обычным насыщенным паром: например, при Т < Т0 давление не зависит от объема системы, что для идеального газа необычно.
Явление, предсказанное Эйнштейном и индийским физиком Бозе много лет назад, впервые экспериментально наблюдалось в 1995 г. в США. «Газ» из 2 000 атомов рубидия, охлажденный почти до абсолютного нуля (20 нК), «сконденсировался» в «суператом», который вел себя уже не как газ частиц, но как единое целое. Таким образом, было создано новое состояние вещества, никогда ранее не существовавшее в естественном виде во Вселенной, как было сказано в сообщении об этих работах. В 2001 г. авторам этих экспериментальных работ была присуждена Нобелевская премия.
Явление сверхтекучести. Сверхтекучесть — это свойство жидкого гелия протекать без трения сквозь тонкие капилляры при низких температурах Т < 2,17 К. Явление открыто П.Л. Капицей в 1938 г. (Нобелевская премия была присуждена в 1978 г.). Дальнейшие исследования показали, что в жидком гелии как бы имеются два компонента: нормальный и сверхтекучий. Из-за отсутствия вязкости сверхтекучий гелий не оказывает сопротивления погруженным телам. В сверхтекучем состоянии жидкий гелий проявляет так много необычных свойств, что мы вправе считать сверхтекучий компонент особым состоянием вещества, которое принято обозначать Не II (в отличие от обычного Не I). Упомянем лишь так называемый эффект фонтанирования: при освещении карманным фонарем нижнего конца капилляра, опущенного в жидкий гелий, он нагревается и доля сверхтекучего компонента падает. Избыточное давление заставляет втекать в капилляр сверхтекучий компонент, что приводит к появлению фонтанчика высотой до 30–40 см. Такое перетекание гелия от холодного места к горячему необычно: в нормальных жидкостях все происходит как раз наоборот.
Фазовая диаграмма для гелия представлена на рис. 7.9.
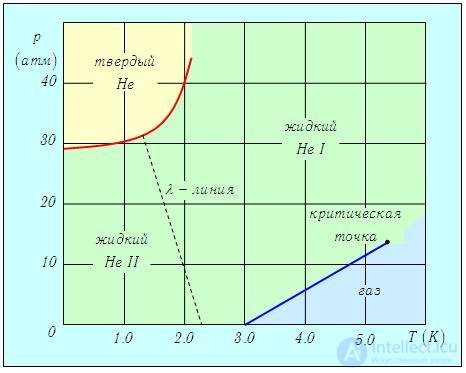
Рис. 7.9. Фазовая диаграмма для 4Не (по осям отложены давление и температура). Штрихами показана l-линия между нормальным (Не I) и сверхтекучим (Не II) состояниями
Фазовый переход Не I => Не II происходит на так называемой l-линии, причем температура перехода уменьшается с ростом давления. Сверхтекучее состояние наблюдалось для изотопа 4Не (сверхтекучесть у другого изотопа 3Не увидели гораздо позже и с большим трудом, но это другая история). Поскольку протон и нейтрон, входящие в ядро гелия, имеют спин 1/2, то спин ядра 4Не — целый, а 3Не — полуцелый. Здесь возникает разница между бозонами и фермионами. Частицы жидкого 4Не — бозоны, и они могут претерпевать конденсацию Бозе — Эйнштейна. К тому же при типичной концентрации частиц в жидкости N/V = 2·1028 м–3, массе ядра гелия т = 6,7·10–27 кг и g = 1 (полный спин ядра равен нулю) формула (8) дает для температуры бозе-эйнштейновской конденсации значение T0 = 2,9 К, что не так далеко от температуры l-перехода. Представляется весьма соблазнительным связать два необычных состояния вещества — бозе-эйнштейновский конденсат и сверхтекучий компонент. Но все не так просто, как кажется.
Элементы микроскопической теории сверхтекучести. Дело в том, что жидкость — не идеальный газ, там имеется сильное взаимодействие между частицами. А мы рассматривали конденсат в системе идеального газа бозонов. И надо еще разобраться, почему конденсат должен проявлять сверхтекучесть. Согласно микроскопической теории Н.Н. Боголюбова (1947), нельзя говорить о состоянии отдельных атомов гелия, но лишь о состоянии всей системы. Здесь мы впервые встречаемся с квантовой жидкостью — макроскопическим квантовым эффектом. При Т = 0 система находится в основном состоянии, при повышении температуры возникают тепловые возбуждения, переход на низколежащие возбужденные уровни энергии. Коллективные возбуждения атомов квантуются аналогично колебаниям атомов кристаллической решетки в теории Дебая. Там при квантовании возникали фононы, здесь — квазичастицы, отдельные кванты с энергией 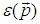 . Оказалось, что первостепенную роль играет закон зависимости энергии от импульса р — закон дисперсии. В квантовой бозе-жидкости «возбуждения» (квазичастицы) — также бозоны с нулевым спином. При низких температурах число квазичастиц мало, и их можно считать невзаимодействующими. В этом случае имеем идеальный газ квазичастиц, который при какой-то критической температуре испытывает конденсацию.
. Оказалось, что первостепенную роль играет закон зависимости энергии от импульса р — закон дисперсии. В квантовой бозе-жидкости «возбуждения» (квазичастицы) — также бозоны с нулевым спином. При низких температурах число квазичастиц мало, и их можно считать невзаимодействующими. В этом случае имеем идеальный газ квазичастиц, который при какой-то критической температуре испытывает конденсацию.
Но все, повторим, зависит от закона дисперсии, полный расчет которого очень сложен и до сих пор не выполнен. Боголюбов вычислил дисперсию слабовозбужденных состояний. В предельных случаях его формула дает
|
|
|
(12) |
где v — некая постоянная с размерностью скорости. Энергия в первом случае есть не что иное, как энергия атома гелия. Энергия же во втором предельном случае аналогична энергии акустического кванта (фонона). Ход кривой показан на рис. 7.10.

Рис. 7.10. Зависимость энергии квазичастиц в Не II от их импульса (закон дисперсии)
Таким образом, при T > 0 жидкий гелий состоит из конденсата квазичастиц и идеального газа квазичастиц с энергией 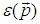 . Атомы гелия нельзя разделить на «образующие конденсат» и «порождающие свободные квазичастицы»: все они принимают участие в образовании как основного конденсатного состояния, так и идеального газа. Газ квазичастиц может рассматриваться как нормальный компонент жидкого гелия, а конденсат — как сверхтекучий. Подобная феноменологическая теория двухкомпонентной жидкости была развита Ландау (1941).
. Атомы гелия нельзя разделить на «образующие конденсат» и «порождающие свободные квазичастицы»: все они принимают участие в образовании как основного конденсатного состояния, так и идеального газа. Газ квазичастиц может рассматриваться как нормальный компонент жидкого гелия, а конденсат — как сверхтекучий. Подобная феноменологическая теория двухкомпонентной жидкости была развита Ландау (1941).
Сверхтекучесть конденсата. Мы разобрались, почему в жидкости может появиться идеальный газ: свободные частицы газа — это не сами атомы гелия, но возбуждения основного состояния (конденсата). Теперь надо понять происхождение сверхтекучести конденсата.
Сначала напомним результаты классической механики, касающиеся перехода к движущимся системам отсчета. Пусть дана система К, в которой радиус-векторы частиц с массами mi обозначены ri. Импульс такой системы есть
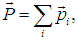
а кинетическая энергия

где
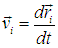 .
.
Пусть дана также система К’, положение начала координат которой задается вектором R, скорость системы К’ относительно К есть
 .
.
В движущейся системе координат радиус-векторы частиц есть
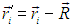
Отсюда немедленно следуют выражения для полного импульса и энергии частиц в движущейся системе координат (М — полная масса всех частиц):
|
|
|
(13) |
Это нерелятивистские преобразования Галилея, известные из классической механики. Следуя рассуждениям Ландау, применим теперь эти формулы к невозбужденному конденсату, текущему по трубке со скоростью V. В лабораторной системе отсчета К энергия и импульс конденсата даются очевидными формулами
|
|
|
(14) |
где Е0 — энергия покоящегося конденсата в основном состоянии. Возьмем систему К’, движущуюся со скоростью конденсата V, так что в ней конденсат покоится. Преобразования Галилея (12) тогда дают
|
|
|
(15) |
Эти результаты очевидны, и мы напомним только, что все это относится к конденсату в основном состоянии. В системе К’ он покоится, а мимо него со скоростью V движется трубка. Если есть вязкость, то она проявится в диссипации энергии. Это не может сразу произойти во всей жидкости: сначала возбудятся отдельные внутренние движения, появятся квазичастицы типа фононов. Пусть возникло возбуждение с импульсом р и энергией 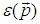 . Для возбужденного конденсата в К’ имеем вполне очевидные соотношения
. Для возбужденного конденсата в К’ имеем вполне очевидные соотношения
|
|
|
(16) |
Как эти формулы будут выглядеть в лабораторной системе отсчета? Чтобы перейти назад в К, используем обратные преобразования Галилея:
|
|
|
(17) |
откуда находим
|
|
|
(18) |
Сравнивая формулы (14) и (18), находим изменение энергии движущегося конденсата в лабораторной системе К при переходе из основного состояния в возбужденное:
|
|
|
(19) |
Образование квазичастицы энергетически выгодно, если ∆Е < 0. В самом благоприятном для этого случае импульс р антипараллелен скорости V, и изменение энергии конденсата равно
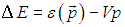
Отсюда следует, что для торможения жидкости необходимо выполнение условия
|
|
|
(20) |
Здесь мы ввели обозначение u* для параметра с размерностью скорости — отношения минимума энергии возбуждения к импульсу. Этот параметр равен тангенсу угла наклона штриховой линии на рис. 3. Если спектр возбуждений таков, что u*>0, как это и показано, то условие торможения не выполняется при слабых возбуждениях: как говорят, в спектре возбуждения имеется энергетическая щель — некая разность между энергией возбуждения и энергией основного состояния. Это значит, что при малых скоростях V < u* трение невозможно. Иными словами, мы получили явление сверхтекучести (при малых импульсах скорость u* равна скорости звука). Смысл полученного результата в том, что конденсат — это коллективное образование, реагирующее на выпадение одного из своих членов повышением энергии, в то время как трение должно энергию понижать. Закон дисперсии, изображенный на рис. 3, таков, что условие сверхтекучести выполнено. Для обычных бозе-частиц с
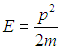
имеем

и условие сверхтекучести не выполнено.
Вывод: обычные частицы даже в конденсатном состоянии сверхтекучестью не обладают, конденсат не образует связанного коллектива и не реагирует на замедление отдельных частиц.
Еще раз подчеркнем: Не II — не смесь различных веществ, и его компоненты невозможно выделить по отдельности. Лучше было бы говорить об одновременном сосуществовании в гелии не компонентов, а двух видов движения — нормального и сверхтекучего.
Сверхпроводимость.

Рис. 7.11. Хейке Камерлинг-Оннес
В 1911 г. голландский физик Г. Камерлинг-Оннес (рис. 7.11) открыл удивительное явление. При температуе около 4 К электрическое сопротивление ртути скачком уменьшалось до нуля. Впоследствии явление сверхпроводимости было обнаружено им у олова, свинца, таллия и других веществ. Были проведены многочисленные эксперименты по выявлению свойств сверхпроводящего состояния вещества.
Важнейшими свойствами сверхпроводящего состояния вещества являются:
Для большинства известных ранее веществ критические температуры имеют порядок 1–15 К. В 1986 г. были открыты керамические соединения, переходящие в сверхпроводящее состояние при температурах порядка 125 К, то есть выше точки кипения жидкого азота. Поскольку ранее сверхпроводники получались лишь при охлаждении материала жидким гелием, а жидкий азот гораздо дешевле в производстве, открытие высокотемпературной сверхпроводимости сулит развитие многочисленных технических приложений.
Критическое значение индукции магнитного поля Вс, при котором происходит разрушение сверхпроводящего состояния, зависит от температуры сверхпроводника. Характерный график зависимости показан на рис. 7.12; он хорошо описывается формулой
|
|
|
(21) |
где В0 — критическое значение поля при абсолютном нуле температуры.
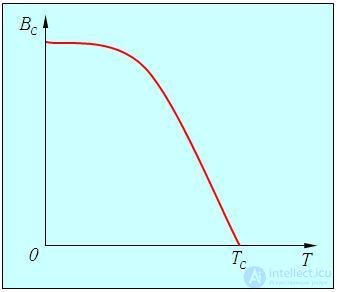
Рис. 7.12. Значение критического магнитного поля как функция температуры сверхпроводника
Как мы увидим далее в нашем курсе, теплоемкость нормального металла при низких температурах имеет вид
|
|
|
(22) |
где первое слагаемое — уже знакомый нам вклад кристаллической решетки, описываемый теорией Дебая, а второе слагаемое - изучаемый в следующей части курса вклад электронного газа. В сверхпроводнике теплоемкость при очень низких температурах определяется, как показывают эксперименты, выражением типа
|
|
|
(23) |
Первое слагаемое не изменилось: кристаллическая решетка по-прежнему на месте. Драматическое изменение второго слагаемого (экспонента вместо линейной функции) показывает, что сверхпроводимость связана с какими-то коренными изменениями поведения электронов проводимости.
Микроскопическая теория сверхпроводимости была создана Д. Бардиным, Л. Купером и Д. Шрифером и усовершенствована Н.Н. Боголюбовым. Она слишком сложна для изложения в данном учебнике. Достаточно лишь указать на то, что имеется глубокая аналогия между сверхтекучестью и сверхпроводимостью. Из-за взаимодействия электронов с фононами между электронами возникает притяжение, и при определенных условиях может образоваться своеобразное связанное состояние — куперовская пара электронов с противоположными спинами. Такое образование является уже бозоном и может испытывать бозе-эйнштейновскую конденсацию, что и является предпосылкой перехода материала в сверхпроводящее состояние.
При абсолютном нуле температуры электронный газ в сверхпроводнике переходит в основное состояние, обладающее свойствами конденсата. Что очень важно, это состояние отделено энергетической щелью Е от следующего, возбужденного, состояния. Иначе говоря, чтобы вывести электрон из основного состояния, надо придать ему некоторую минимальную энергию Еg, а меньшие порции энергии просто не будут восприняты. Нечто подобное мы уже видели для сверхтекучего состояния, а еще ранее — для теплоемкости («замораживание» вращательных и колебательных степеней свободы, теория теплоемкости Эйнштейна). Теория предсказывает простую связь энергетической щели и критической температуры:
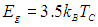
Наличие энергетической щели сразу объясняет поведение теплоемкости электронного газа. Действительно, энергия Еg — это минимальная энергия, разрушающая куперовскую пару, и сообщение такой энергии порождает пару свободных электронов. Тогда на каждый электрон приходится половинная энергия Eg/2. Из статистических соображений можно утверждать, что число электронов вне основного состояния пропорционально величине
 .
.
Тепловая энергия, поглощаемая при возбуждении, пропорциональна
 .
.
Производная этой величины по температуре дает теплоемкость электронного газа в сверхпроводящем состоянии:
|
|
|
(24) |
При низких температурах предэкспоненциальный множитель 1/Т2 меняется гораздо медленнее экспоненты, так что этот закон практически не отличается от феноменологического соотношения (23). При изменении температуры величина щели изменяется по закону, похожему на изображенный на рис. 4. При критической температуре щель исчезает, и вместе с ней исчезают сверхпроводящие свойства. Заметим, что выражение (24) аналогично формуле для теплоемкости (7.8) в теории Эйнштейна, где также имеется щель между основным и возбужденным уровнями энергии.
Из сказанного ясно, какую важную роль играет энергетическая щель. В системе бозонов она ответственна за явления сверхтекучести и сверхпроводимости. В системе фермионов, как мы увидим в дальнейшем, она ответственна за различие свойств металлов, диэлектриков и полупроводников.
Исследования явлений сверхтекучести и сверхпроводимости всегда вызывали большой интерес как ученых, так и общества в целом. «Виной» тому — широкие перспективы их практического использования. Особое значение они приобретают в современном мире, где ученые научились создавать совершенно новые материалы с необычными характеристиками, проявляющие, например, сверхпроводящие свойства при относительно высоких температурах и в достаточно сильных магнитных полях. Не случайно за исследования в этой области присуждена не одна Нобелевская премия, начиная с Камерлинг-Оннеса (премия 1913 г.) и заканчивая пока премией 2003 г., которую получили А.А. Абрикосов (Россия и США), В.Л. Гинзбург (Россия) и Э. Леггетт (Великобритания и США).
Исследование, описанное в статье про теплоемкость кристаллов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теплоемкость кристаллов, квантовая статистика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика