Лекция
Привет, Вы узнаете о том , что такое трение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое трение, законы трения, явление застоя, кривая штрибека , настоятельно рекомендую прочитать все из категории Базовая физика.
Тре́ние — процесс механического взаимодействия соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение ) либо при относительном смещении параллельных слоев жидкости, газа или деформируемого твердого тела (внутреннее трение, или вязкость). Далее в этой статье под трением понимается лишь внешнее трение. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз .
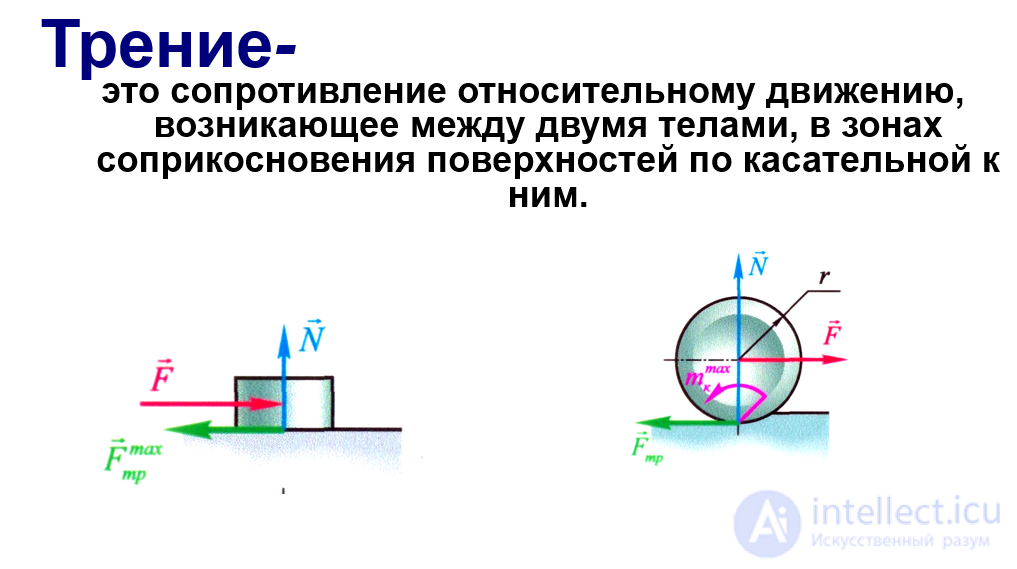
Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей. Сила трения зависит от материала трущихся поверхностей и от того, насколько сильно эти поверхности прижаты друг к другу. В простейших моделях трения (закон Кулона для трения) считается, что сила трения прямо пропорциональна силе нормальной реакции между трущимися поверхностями. В целом же, в связи со сложностью физико-химических процессов, протекающих в зоне взаимодействия трущихся тел, процессы трения принципиально не поддаются описанию с помощью простых моделей классической механики.
сила механического сопротивления, возникающая в плоскости соприкосновения двух прижатых друг к другу тел при их относительном перемещении.
Сила сопротивления, действующая на тело, направлена противоположно относительному перемещению данного тела.
Сила трения возникает по двум причинам:
1) первая и основная причина заключается в том, что в местах соприкосновения молекулы веществ притягиваются друг к другу, и для преодоления их притяжения требуется совершить работу. Соприкасающиеся поверхности касаются друг друга лишь в очень небольших по площади местах. Их суммарная площадь составляет 0,01-:0,001 от общей (кажущейся) площади соприкосновения. При скольжении площадь реального соприкосновения не остается неизменной. Сила трения (скольжения) будет изменяться в процессе движения. Если тело, которое скользит, прижать сильнее к телу, по которому происходит скольжение, то вследствие деформации тел площадь пятен соприкосновения (и сила трения) увеличится пропорционально прижимающей силе.
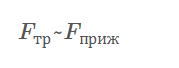
2) вторая причина возникновения силы трения – это наличие шероховатостей (неровностей) поверхностей, и деформация их при движении одного тела по поверхности другого. Глубина проникновения (зацепления) шероховатостей зависит от прижимающей силы, а от этого зависит и величина деформаций.
Последние, в свою очередь, определяют величину силы трения: 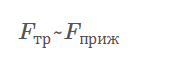 .
.
При относительном скольжении обе причины имеют место, потому характер взаимодействия имеет вид простого соотношения:
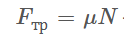 – сила трения скольжения (формула Кулона – Амонтона), где
– сила трения скольжения (формула Кулона – Амонтона), где
μ – коэффициент трения скольжения,
N – сила реакции опоры, равная прижимающей силе.
Величина коэффициента трения различна для разных комбинаций трущихся веществ даже при одинаковой их обработке (силы притяжения и упругие свойства зависят от рода вещества).
Если между трущимися поверхностями будет находится смазка, то сила притяжения изменится заметным образом (будут притягиваться другие молекулы, и сила трения скольжения частично заменится силой вязкого трения, которую мы рассмотрим ниже).
Если на тело, лежащее на горизонтальной поверхности, действует горизонтальная сила `vecF`, то движение будет вызвано этой силой только в том случае, когда она станет больше некоторого значения `(muN)`. До начала движения внешняя сила скомпенсирована силой трения покоя. Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения, и деформации шероховатостей.
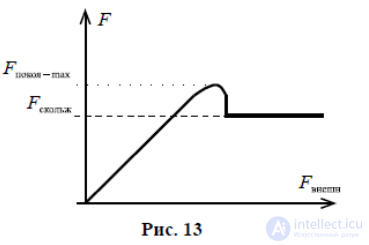
Сила трения покоя различна в разных участках поверхности, по которой будет происходить движение. Если тело долго лежит на поверхности, то вследствие вибраций (они всегда присутствуют на поверхности Земли) площадь пятен соприкосновения незначительно увеличится. Поэтому для начала движения придется преодолеть немного большую силу трения, чем сила трения скольжения. Данное явление называется явлением застоя.
Это явление встречается в:
тормозных системах (визг тормозов),
землетрясениях (накопление и срыв напряжения в тектонических плитах),
механике (скрип дверей, дрожание механизмов).
явление застоя (stick-slip) при движении смычка по струне — это чередование фаз прилипания и срыва: Смычок прилипает к струне (трение покоя), натягивая ее. Струна срывается (трение скольжения) и вибрирует, создавая звук.Именно это явление позволяет скрипке звучать чисто и выразительно. Этот цикл повторяется сотни раз в секунду, формируя устойчивое звучание.
С этим явлением мы сталкиваемся, например, передвигая мебель в комнате. (На рисунке 13 превосходство трения покоя над трением скольжения сильно преувеличено).
Силой трения покоя мы пользуемся для перемещения на лыжах или просто при ходьбе.
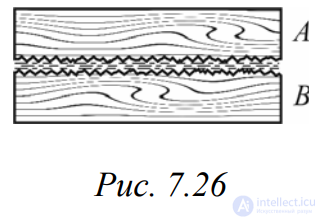
Рассмотренные виды силы трения относятся к сухому трению или внешнему. Но есть еще один вид силы трения – вязкое трение.
При движении тела в жидкости или газе происходят достаточно сложные процессы обмена молекулами между слоями обтекающей жидкости или газа. Эти процессы называют процессами переноса.
При небольших скоростях движения тела относительно газа или жидкости сила сопротивления будет определяться выражением:
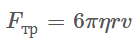 – закон Стокса для шара, где
– закон Стокса для шара, где
η - вязкость вещества, в котором движется тело;
r - средний поперечный размер (радиус) тела;
ν - относительная скорость тела;
6π - коэффициент, соответствующий сферической форме тела.
Вывод о величине скорости (большая она или маленькая) можно сделать, определив безразмерный коэффициент, называемый числом Рейнольдса:
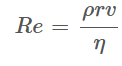 ` - число Рейнольдса, где
` - число Рейнольдса, где
ρ - плотность вещества, в которой движется тело.
Если Re<1700, то движение газа (жидкости) вокруг тела ламинарное (слоистое), и скорости можно считать малыми.
Если Re>1700, то движение газа (жидкости) вокруг тела турбулентное (с завихрениями), и скорости можно считать большими.
В последнем случае на образование вихрей тратится большая часть кинетической энергии тела, а значит, сила трения становится большей, а зависимость перестает быть линейной.
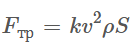 - сила вязкого трения при больших скоростях, где
- сила вязкого трения при больших скоростях, где
S - площадь поперечного сечения тела,
k - постоянная величина, зависящая от поперечных размеров тела.
Часто последнюю формулу можно видеть в виде:
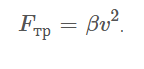
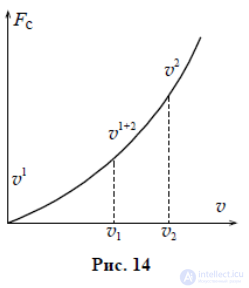
Число Рейнольдса, выбранное равным `1700`, в действительности определяется конкретной задачей (условиями) и может принимать другие значения того же порядка. Объясняется это тем, что зависимость силы вязкого трения от скорости носит сложный характер: при некотором значении скорости v1 линейная зависимость начинает нарушаться, а при некотором значении скорости v2 эта зависимость становится квадратичной. В промежутке от v1 до v2 степень принимает дробные значения (рис. 14). Число Рейнольдса характеризует состояние динамической системы, при котором движение слоев остается ламинарным, и сильно зависит от внешних условий. К примеру: стальной шар, двигаясь в воде вдали от границ жидкости (в океане, озере) сохраняет ламинарным движение слоев при Re=1700, а тот же шар, движущийся в вертикальной трубе немного большего, чем шар, радиуса, заполненной водой, уже при Re=2 вызовет появление завихрений воды вокруг шара. (Отметим, что число Рейнольдса не единственное, применяемое для описания подобного движения. Например, применяют еще числа Фруда и Маха.)
Из-за такой сложной зависимости силы сопротивления от размеров, формы тела и его скорости рассчитать с необходимой точностью силу сопротивления невозможно. Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путем, продувая воздух в аэродинамических трубах.
Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению скорости на радиус капель: F=krv
. Капли радиуса 0,1 мм, падая с большой высоты, у земли имеют скорость около 1 м/с.
Какую скорость будут иметь капли, радиус которых в два раза меньше?
В десять раз меньше?
Капля падает с постоянной скоростью, т. к. сила тяжести скомпенсирована силой вязкого трения о воздух:
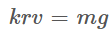 или
или 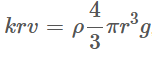 `, откуда
`, откуда 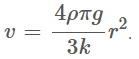 .
.
Из полученного результата следует, что скорость капли прямо пропорциональна квадрату радиуса. Если радиус капли уменьшится в два раза, то скорость ее падения уменьшится в четыре раза, и составит `v_1~~0,25` м/с; а если радиус окажется в десять раз меньше, то скорость будет в сто раз меньше, т. е. v2~0,01 м/с.
Задача любопытна тем, что может объяснить почему облака не падают. Ведь облака – это туман, который не падает из-за наличия восходящих потоков воздуха. На нижней границе облака находятся наиболее крупные капли. Поднимаясь, скорость потока уменьшается, т. к. он совершает работу над встретившимся воздухом и увеличивает свою потенциальную энергию. Раз скорость потока в верхней части облака меньше, то и размер капель там тоже меньше. Капли «висят» над поверхностью земли на постоянной высоте.
При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:

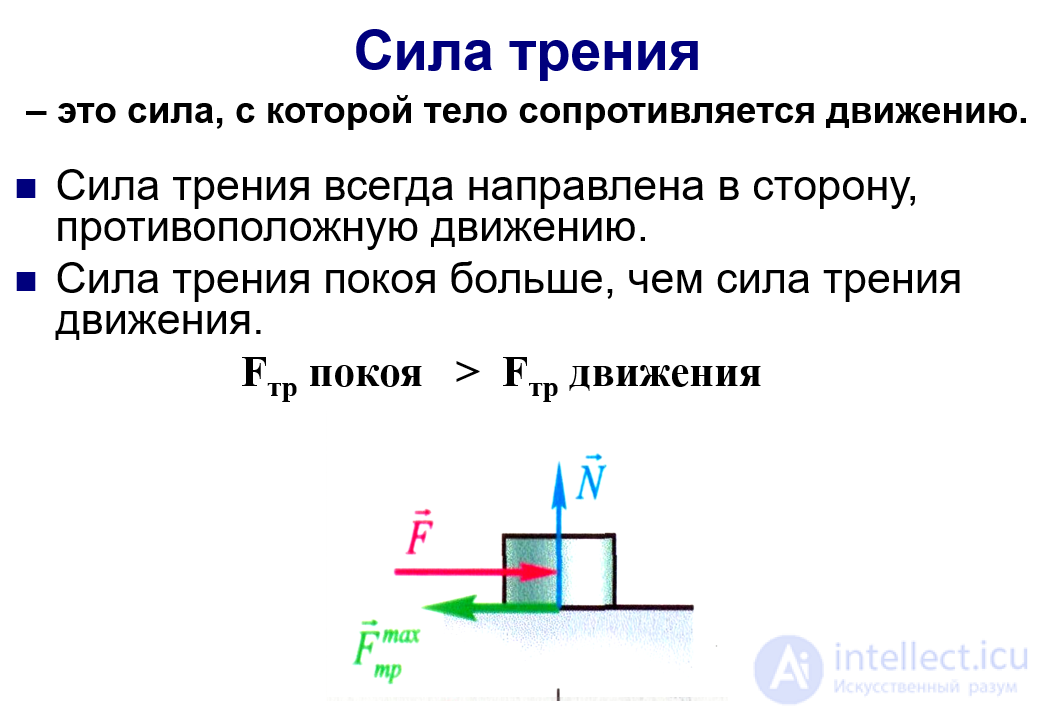
В физике взаимодействие трения принято разделять на:
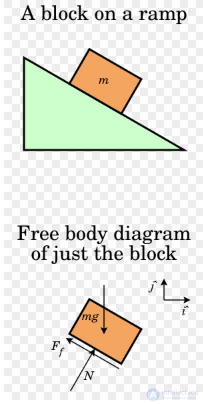
Схема свободного тела для блока на пандусе. Стрелки — это векторы, указывающие направления и величины сил. N — сила реакции опоры, mg — сила тяжести, а Ff — сила трения.
Сила нормальной реакции определяется как результирующая сила, сжимающая две параллельные поверхности вместе, а ее направление перпендикулярно этим поверхностям. В простом случае, когда масса лежит на горизонтальной поверхности, единственной составляющей нормальной силы является сила тяжести, где N=mg . В этом случае условия равновесия говорят нам, что величина силы трения равна нулю, . Фактически сила трения всегда удовлетворяет условию
, причем равенство достигается только при критическом достаточно крутом угле рампы (определяемом формулой
) для начала скольжения.
Коэффициент трения — это эмпирическое (экспериментально измеренное) структурное свойство, которое зависит только от различных аспектов контактирующих материалов, таких как шероховатость поверхности. Коэффициент трения не зависит от массы или объема. Например, большой алюминиевый блок имеет тот же коэффициент трения, что и маленький алюминиевый блок. Однако величина самой силы трения зависит от силы реакции опоры и, следовательно, от массы блока.

Коэффициент fтр трения скольжения (при покое) определяют опытным путем: значения его для различных условий приведены в справочниках.
Металл по металлу без смазки .............. 0,15. ..0,3
То же, со смазкой ................... ................ 0,1. ..0,18
Дерево по дереву без смазки .................. 0,4.. .0,6
Кожа по чугуну без смазки ..................... 0,3. ..0,5
То же, со смазкой .................................... 0,15
Сталь по льду ........................................... 0,02
Коэффициент трения скольжения при движении обычно меньше, чем при покое, и в первом приближении не зависит от скорости относительного перемещения тел.
В зависимости от ситуации расчет нормальной силы N включает в себя силы, отличные от силы тяжести. Если объект находится на ровной горизонтальной поверхности и подвергается воздействию внешней силы P, тогда она заставляет его скользить, когда сила нормальной реакции между объектом и поверхностью выражается равенством
, где mg — вес блока и
— составляющая внешней силы, направленной вниз. Перед скольжением эта сила трения равна
, где Px — горизонтальная составляющая внешней силы. Таким образом,
. Скольжение начинается только после того, как сила трения достигает значения
. А до тех пор трение обеспечивает равновесие, поэтому его можно рассматривать просто как реакцию.
Если объект находится на наклонной поверхности, например на наклонной плоскости, нормальная (к поверхности) сила тяжести меньше, чем mg, потому что меньшая сила тяжести перпендикулярна грани плоскости. Нормальная сила и сила трения в конечном итоге определяются с помощью векторного анализа, обычно с помощью диаграммы Максвелла — Креионы.
В общем, процесс решения любой статической задачи с трением состоит в том, чтобы рассматривать соприкасающиеся поверхности предварительно как неподвижные, чтобы можно было рассчитать соответствующую тангенциальную силу реакции между ними. Если эта сила реакции удовлетворяет , то предварительное предположение было правильным, и это действительная сила трения. В противном случае силу трения необходимо установить равной
, а затем результирующий дисбаланс сил будет определять ускорение, связанное со скольжением.
Коэффициент трения, часто обозначаемый греческой буквой µ, представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения. Коэффициент трения зависит от используемых материалов; например, лед имеет низкий коэффициент трения о сталь, а резина — высокий коэффициент трения при скольжении по дорожному покрытию. Коэффициенты трения находятся в диапазоне от почти нуля до значений больше единицы. Трение между двумя металлическими поверхностями из одинаковых металлов больше, чем между двумя из разных — следовательно, латунь будет иметь более высокий коэффициент трения при движении по латуни, но меньше чем при движении по стали или алюминию .
Для поверхностей в состоянии покоя относительно друг друга , где
— коэффициент статического трения. Обычно он больше, чем его кинетический аналог. Коэффициент статического трения, проявляемый парой контактирующих поверхностей, зависит от совокупного воздействия характеристик деформации материала и шероховатости поверхности, оба из которых берут свое начало в химической связи между атомами в каждом из объемных материалов, а также между поверхностями материала и любыми другими адсорбированными материалами. Известно, что фрактальность поверхностей, параметр, описывающий масштабное поведение неровностей поверхности, играет важную роль в определении величины статического трения .
Для поверхностей, находящихся в относительном движении , где
— коэффициент кинетического трения. Кулоновское трение равно
, и сила трения на каждой поверхности действует в направлении, противоположном ее движению относительно другой поверхности.
Артур Морин ввел этот термин и продемонстрировал полезность коэффициента трения . Коэффициент трения — это эмпирическая величина — его нужно измерить экспериментально и он не может быть определен путем расчетов . Более грубые поверхности обычно имеют более высокие эффективные значения коэффициента трения. Как статические, так и кинетические коэффициенты трения зависят от пары контактирующих поверхностей; для данной пары поверхностей коэффициент трения покоя обычно больше, чем коэффициент кинетического трения; в некоторых наборах два коэффициента равны, например, тефлон на тефлоне.
Большинство сухих материалов имеют значения коэффициента трения от 0,3 до 0,6. Значения вне этого диапазона встречаются реже, но тефлон, например, может иметь коэффициент всего 0,04. Нулевое значение означало бы отсутствие трения, ненаблюдаемое свойство. Резина при контакте с другими поверхностями может иметь коэффициент трения от 1 до 2. Иногда утверждают, что μ всегда <1, но это неверно. В то время как в большинстве соответствующих приложений μ <1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальное усилие поверхности на объект. Например, поверхности, покрытые силиконовым каучуком или акриловым каучуком, имеют коэффициент трения, который может быть значительно больше 1.
Хотя часто утверждается, что коэффициент трения является «материальным свойством», его лучше классифицировать как «системное свойство». В отличие от истинных свойств материала (таких как проводимость, диэлектрическая проницаемость, предел текучести), коэффициент трения для любых двух материалов зависит от системных переменных, таких как температура, скорость, атмосфера, а также от того, что сейчас обычно называют временем старения и разрушения; а также от геометрических свойств границы раздела материалов, а именно структуры их поверхностей . Например, медный штифт, скользящий по толстой медной пластине, может иметь коэффициент трения, который изменяется от 0,6 при низких скоростях (скольжение металла по металлу) до менее 0,2 при высоких скоростях, когда поверхность меди начинает плавиться из-за нагрева от трения. Последняя скорость, конечно, не определяет коэффициента трения однозначно; если диаметр штифта увеличивается так, что нагрев от трения быстро устраняется, температура падает, и штифт остается твердым, а коэффициент трения повышается до значения, наблюдаемого при испытании на «низкой скорости».
При определенных условиях некоторые материалы имеют очень низкие коэффициенты трения. Примером является (высокоупорядоченный пиролитический) графит, который может иметь коэффициент трения ниже 0,01 . Этот режим сверхнизкого трения называется сверхсмазкой.
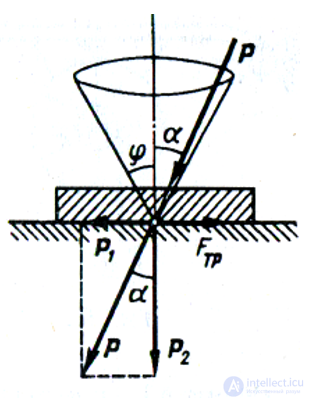
Если коэффициент трения скольжения одинаков для всех направлений движения, то множество полных реакций образует круговой конус трения
Для равновесия тела, лежащего на шероховатой поверхности, равнодействующая приложенных к нему активных сил должна проходить внутри конуса трения.
По второму закону трения скольжения
Fтр = fтр Р2=Р2 tg j Следовательно, при α < φ будет Р1
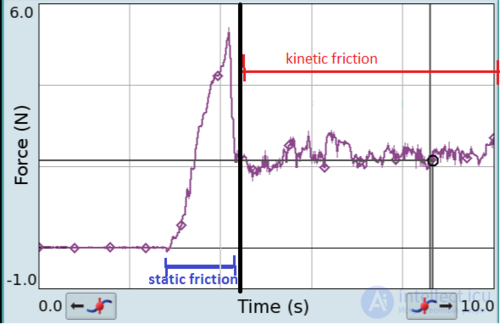
Когда масса неподвижна, то объект испытывает статическое трение. Трение увеличивается по мере увеличения приложенной силы, пока блок не переместится. После того, как блок начнет перемещение, он испытывает кинетическое трение, которое меньше максимального статического трения.
Статическое трение — это трение между двумя или более твердыми объектами, которые не движутся относительно друг друга. Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μs, обычно выше, чем коэффициент кинетического трения. Считается, что статическое трение возникает в результате особенностей шероховатости поверхности на различных масштабах длины на твердых поверхностях. Эти особенности, известные как неровности, присутствуют вплоть до наноразмеров и приводят к тому, что настоящий контакт твердого тела с твердым телом существует только в ограниченном количестве точек, составляющих лишь часть видимой или номинальной площади контакта . Линейность между приложенной нагрузкой и истинной площадью контакта, возникающая из-за деформации неровностей, приводит к линейности между статической силой трения и нормальной силой, обнаруживаемой для типичного трения Амонтона — Кулона .
Сила статического трения должна быть преодолена приложенной силой, прежде чем объект сможет двигаться. Максимально возможная сила трения между двумя поверхностями до начала скольжения является произведением коэффициента трения покоя и нормальной силы: . Когда скольжения не происходит, сила трения принимает любое значение от нуля до Fmax . Любая сила меньше чем Fmax пытающаяся сдвинуть одну поверхность по другой встречает противодействие силы трения равной величины и противоположной по направлению. Любая сила больше, чем Fmax преодолевает силу статического трения и вызывает скольжение. Происходит мгновенное скольжение, статическое трение больше не применяется — трение между двумя поверхностями тогда называется кинетическим трением. Однако кажущееся трение покоя может наблюдаться даже в том случае, когда истинное трение покоя равно нулю .
Примером статического трения может служить сила, препятствующая скольжению автомобильного колеса при качении по земле. Несмотря на то, что колесо находится в движении, участок шины, контактирующий с землей, неподвижен относительно земли, поэтому это статическое, а не кинетическое трение.
Максимальное значение статического трения иногда называют ограничивающим трением, хотя этот термин не используется повсеместно .
Кинетическое трение, также известное как трение скольжения, возникает, когда два объекта движутся относительно друг друга и трутся друг о друга (как салазки по земле). Коэффициент кинетического трения обычно обозначается как μk и обычно меньше коэффициента трения покоя для тех же материалов . Однако Ричард Фейнман отмечает, что «с сухими металлами очень трудно показать какое-либо различие». Сила трения между двумя поверхностями после начала скольжения является произведением коэффициента кинетического трения и силы реакции опоры: . Это отвечает за кулоновское демпфирование колеблющейся или вибрирующей системы.
Новые модели показывают, насколько кинетическое трение может быть больше, чем трение покоя. Кинетическое трение, во многих случаях, в первую очередь вызвано химической связью между поверхностями, а не переплетенными неровностями ; однако во многих других случаях эффекты шероховатости являются доминирующими, например, при трении резины о дорогу. Шероховатость поверхности и площадь контакта влияют на кинетическое трение для микро- и наноразмерных объектов, где силы, распределенные по площади поверхности, преобладают над силами инерции .
Происхождение кинетического трения в наномасштабе можно объяснить термодинамикой . При скольжении новая поверхность образуется в задней части скользящего истинного контакта, а существующая поверхность исчезает в передней части. Поскольку все поверхности включают в себя термодинамическую поверхностную энергию, работа должна быть затрачена на создание новой поверхности, а энергия выделяется в виде тепла при удалении поверхности. Таким образом, требуется сила, чтобы переместить заднюю часть контакта, и тепло трения выделяется спереди.
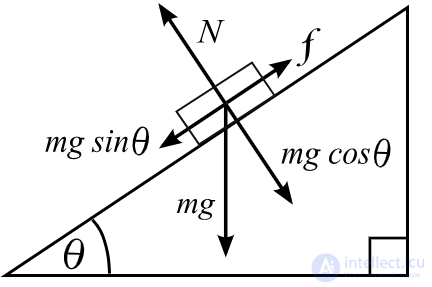
Угол трения θ, когда блок только начинает скользить.
Для некоторых приложений более полезно определять статическое трение в терминах максимального угла, перед которым один из элементов начнет скользить. Он называется углом трения и определяется как:
где θ — угол от горизонтали, а μs — статический коэффициент трения между телами . Эту формулу также можно использовать для расчета μs на основе эмпирических измерений угла трения.
Определение сил, необходимых для перемещения атомов друг мимо друга, является сложной задачей при разработке наномашин. В 2008 году ученые впервые смогли переместить отдельный атом по поверхности и измерить необходимые силы. Используя сверхвысокий вакуум и почти низкую температуру (5 К), при помощи модифицированного атомно-силового микроскопа перемещались атомы кобальта и молекулы монооксида углерода по поверхности меди и платины .
Fтр =fтр N= fтр G2= fтр G cos a
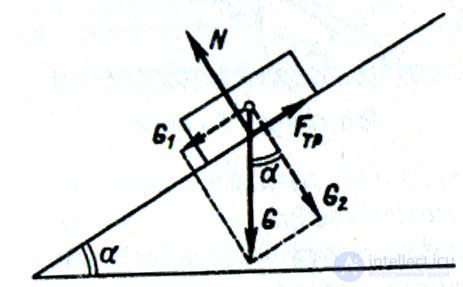
Fтр = fтр mg cos a
а) Если угол наклона плоскости равен углу трения (α = φ), то тело, лежащее на наклонной поверхности, будет под действием собственной силы тяжести либо равномерно скользить, либо находится в покое
б)Если α < φ – тело находится в покое
в)Если α > φ – тело будет под действием собственной силы тяжести равномерно скользит
Трение качения вызвано деформацией поверхности качения, при этом деформируется и само катящееся тело.
Трение качения возникает при попытке «перекатить» друг относительно друга тела с криволинейной поверхностью
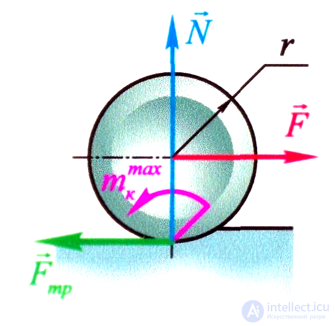
КАТОК И ТРЕНИЕ КАЧЕНИЯ
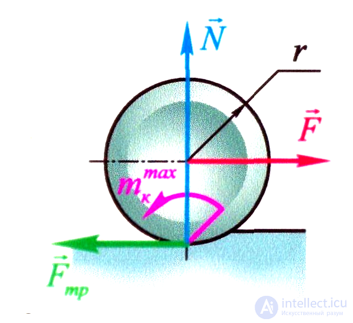
Колесо катится под действием момента качения
Мк = F r,
где Мк - момент качения;
F - внешняя сила
r - радиус колеса.
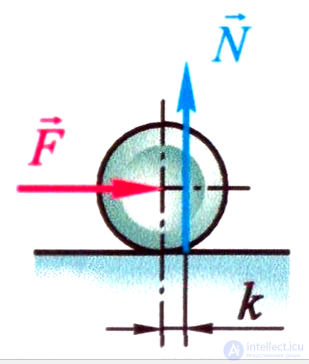
При качении возникает трение качения за счет пары трения качения с моментом Мкmax
Мкmax = k N,
где Мкmax – момент трения качения;
k – коэффициент трения качения – это расстояние между вектором силы тяжести и смещенной точкой опоры (размерная величина [м]);
N – сила нормального давления из смещен- ной точкой опоры
ВОЗМОЖНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТЕЛА
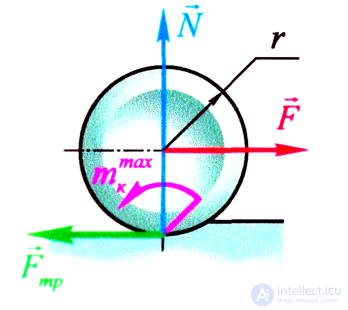
Тело катится, только если Мк ≥ Мкmax, т.е. F r ≥ k N
Минимальная сила необходимая для движения F = k N /r
Чем больше радиус r, тем меньше сила F
а) Мк ≥ Мкmax, но F < Fтр - тело только катится
б) Мк < Мкmax, но F > Fтр - тело только скользи
в) Мк > Мкmax, но F > Fтр - тело катится с проскальзыванием
г) Мк < Мкmax, но F < Fтр - тело в состоянии покоя
законы трения
Существуют три закона трения скольжения (законы Кулона):
1.Сила трения не зависит от величины площади трущихся поверхностей
Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление и сопротивление останется прежним.
2.Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела.
Во сколько раз увеличится сила нормального давления или реакция, во столько же раз возрастет максимальная сила трения.
Сила трения равна произведению силы нормального давления на коэффициент трения скольжения
(Из второго закона трения)

Fтр=fтр N ,
где fтр - коэффициент трения скольжения
N- сила нормального давления
3.Сила трения зависит от материала тел, состояния трущихся поверхностей, наличия и рода смазки.
Различают фрикционные (специальные пластмассы с применением асбеста и меди) и антифрикционные материалы(баббит, бронза, графит).
Шероховатые поверхности обладают большим трением, чем гладкие.
При смазке поверхностей скольжения тело начинает двигаться с меньшим трением.
Основной характеристикой трения является коэффициент трения μ , определяющийся материалами, из которых изготовлены поверхности взаимодействующих тел.
В простейших случаях сила трения F и нормальная нагрузка (или сила нормальной реакции) Nnormal связаны неравенством
| Пары материалов | μ покоя | μ скольжения |
|---|---|---|
| Сталь-Сталь | 0,5—0,8 | 0,15—0,18 |
| Резина-Сухой асфальт | 0,95—1 | 0,5—0,8 |
| Резина-Влажный асфальт | 0,25—0,75 | |
| Лед-Лед | 0,05—0,1 | 0,028 |
| Резина-Лед | 0,3 | 0,15—0,25 |
| Стекло-Стекло | 0,9 | 0,7 |
| Нейлон-Нейлон | 0,15—0,25 | |
| Полистирол-Полистирол | 0,5 | |
| Плексиглас, оргстекло | 0,8 |
Для большинства пар материалов значение коэффициента трения μ не превышает 1 и находится в диапазоне 0,1 — 0,5. Если коэффициент трения превышает 1
, это означает, что между контактирующими телами имеется сила адгезии Nadhesion
и формула расчета коэффициента трения меняется на
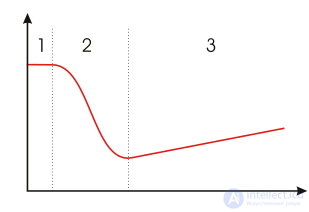
Кривая Штрибека
Кривая Штрибека — это кривая, выражающая зависимость силы трения скольжения F от величины скорости v . Применяется в теории гидродинамического трения. Установлена в 1902 году немецким исследователем Рихардом Штрибеком . По мнению первооткрывателя, закон, выражаемый этой кривой, также относится к упрочнению материалов и теории опор валов.
Свойства На кривой Штрибека принимаются во внимание
Если относительное движение не происходит, то имеет место трение покоя. После того, как к системе приложена сила, превосходящая критическое значение трения FH , начинается относительное движение. Трение почти неизменно и изначально мало зависит от скорости, пока во вновь образовавшихся областях контакта молекулы смазочного материала полностью вытеснены. В этом случае говорят о сухом, или граничном трении (область 1). Если это не так, и хоть какое количество смазочного материала отделяет одно тело от другого, то трение резко уменьшается (область 2). При значениях скорости, превосходящих некоторое критическое значение (Ausklinkpunkt), сила сопротивления начинает возрастать с возрастанием скорости по закону, близкому к линейному (область 3). В этом случае говорят о гидродинамическом или об упруго-гидродинамическом трении (эласто-гидродинамическое трение). Как правило, в области гидродинамического трения износ является наименьшим.
Трение является важным фактором во многих инженерных дисциплинах.
Трение в механизмах и машинах
В большинстве традиционных механизмов (ДВС, автомобили, зубчатые шестерни и пр.) трение играет отрицательную роль, уменьшая КПД механизма. Для уменьшения силы трения используются различные натуральные и синтетические масла и смазки. В современных механизмах для этой цели используется также напыление покрытий (тонких пленок) на детали. С миниатюризацией механизмов и созданием микроэлектромеханических систем (МЭМС) и наноэлектромеханических систем (НЭМС) величина трения по сравнению с действующими в механизме силами увеличивается и становится весьма значительной (μ⩾1) , и при этом не может быть уменьшена с помощью обычных смазок, что вызывает значительный теоретический и практический интерес инженеров и ученых к данной области. Для решения проблемы трения создаются новые методы его снижения в рамках трибологии и науки о поверхности.
Наличие трения обеспечивает возможность перемещаться по поверхности. Так, при ходьбе именно за счет трения происходит сцепление подошвы с полом, в результате чего происходит отталкивание от пола и движение вперед. Точно так же обеспечивается сцепление колес автомобиля (мотоцикла) с поверхностью дороги. В частности, для улучшения этого сцепления разрабатываются новые формы и специальные типы резины для покрышек, а на гоночные болиды устанавливаются антикрылья, сильнее прижимающие машину к трассе.
Греки, в том числе Аристотель, Витрувий и Плиний Старший интересовались причиной и снижением трения . Они знали о различиях между статическим и кинетическим трением, а Фемистий утверждал в 350 году, что «легче продолжать движение движущегося тела, чем перемещать тело в состоянии покоя» .
Классические законы трения скольжения были открыты Леонардо да Винчи в 1493 году, который был пионером в области трибологии, но законы, задокументированные в его записных книжках, не были опубликованы и остались неизвестными . Эти законы были переоткрыты Гийомом Амонтоном в 1699 году и стали известны как три закона Амонтона сухого трения. Амонтон представлял природу трения с точки зрения неровностей поверхности и силы, необходимой для увеличения веса, прижимающего поверхности друг к другу. Эта точка зрения была развита Бернаром Форестом де Белидором и Леонардом Эйлером в 1750 году, которые вывели угол естественного откоса груза на наклонной плоскости и впервые различили статическое и кинетическое трение . Иоанн Теофил Дезагюлье в 1734 году первым осознал роль адгезии в трении. Эти микроскопические силы заставляют поверхности слипаться; и он предположил, что трение — это сила, необходимая для разрыва прилегающих поверхностей.
Понимание трения в дальнейшем развил Шарль-Огюстен де Кулон (1785) . Кулон исследовал влияние четырех основных факторов, влияющих на трение: природы контактирующих материалов и покрытия их поверхностей; протяженность площади поверхности; нормальное давление (или нагрузка); и продолжительность контакта поверхностей (время покоя) . Кулон также рассмотрел влияние скорости скольжения, температуры и влажности, чтобы выбрать между различными икорктическими объяснениями природы трения. Различие между статическим и кинетическим трением появляется в законе трения Кулона, хотя это различие уже было замечено Иоганном Андреасом фон Зегнером в 1758 году . Эффект времени покоя объяснил Питер ван Мушенбрук в 1762 году путем рассмотрения поверхностей волокнистых материалов со сцепляющимися вместе волокнами, что занимает конечное время, в течение которого увеличивается трение.
Джон Лесли (1766—1832) отметил слабость взглядов Амонтона и Кулона: если трение возникает из-за того, что груз поднимается по наклонной плоскости последовательных выступов, то почему тогда оно не уравновешивается движением вниз по противоположному склону? Лесли столь же скептически относился к роли адгезии, предложенной Дезагюлье, которая в целом должна приводить как к ускорению, так и к замедлению движения . По мнению Лесли, трение следует рассматривать как зависящий от времени процесс уплощения, сдавливания неровностей, что создает новые препятствия в тех областях, что раньше было полостями.

Артур-Жюль Морен (1833) разработал концепцию трения скольжения по сравнению с трением качения. Осборн Рейнольдс (1866) вывел уравнение вязкого течения. Это завершило классическую эмпирическую модель трения (статического, кинетического и жидкостного), обычно используемую сегодня в технике . В 1877 году Флеминг Дженкин и Джеймс А. Юинг исследовали непрерывность статического и кинетического трения.

В центре внимания исследований в 20 веке стало понимание физических механизмов трения. Франк Филип Боуден и Дэвид Табор (1950) показали, что на микроскопическом уровне фактическая площадь контакта между поверхностями составляет очень небольшую часть видимой площади . Эта фактическая площадь контакта, вызванная неровностями, увеличивается по мере увеличения давлением. Развитие атомно-силового микроскопа (1986) позволило ученым изучить трение в атомном масштабе показав, что на этом масштабе сухое трение — это продукт межповерхностного сдвигового напряжения и площади контакта. Эти два открытия объясняют первый закон Амонтона; макроскопическая пропорциональность между нормальной силой и статической силой трения между сухими поверхностями.
Исследование, описанное в статье про трение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое трение, законы трения, явление застоя, кривая штрибека и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Базовая физика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика