Вектор и Теорема Пойнтинга, Распространение электромагнитной энергии и ее мощности

Привет, Вы узнаете о том , что такое теоремы пойнтинга, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теоремы пойнтинга, вектор пойнтинга , настоятельно рекомендую прочитать все из категории Переменный электрический ток. Электромагнитное поле.

вектор пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, компоненты которого входят в состав тензора энергии-импульса электромагнитного поля .

Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

(в системе СГС),

(в Международной системе единиц (СИ)),

где E и H — векторы напряженности электрического и магнитного полей соответственно. В СИ величина S имеет размерность Вт/м2.

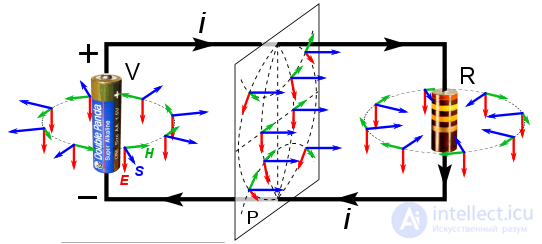
цепь постоянного тока i, соединяющая батарею V с резистором R
вектор Пойнтинга S в пространстве, окружающем цепь
напряженность электрического поля Е
напряженность магнитного поля H
Вокруг батареи вектор Пойнтинга направлен от батареи, что свидетельствует о переносе энергии из батареи; вокруг резистора вектор Пойнтинга направлен к резистору, что говорит о переносе энергии в резистор; поток вектора Пойнтинга через любую плоскость Р между батареей и резистором — направлен от батареи к резистору.

В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усредненной по периоду комплексной плотности потока энергии :

(в системе СГС),

(в системе СИ),

где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае четкий физический смысл имеет только действительная часть комплексного вектора S — это вектор усредненной за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.

Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.

Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.

Вектор Пойнтинга и импульс электромагнитного поля

В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, деленным на квадрат скорости света:

(в системе СИ)

В этом соотношении проявляется материальность электромагнитного поля.

Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объему.

Вектор Пойнтинга в макроскопических средах

В макроскопической среде электромагнитные эффекты описываются пространственно-усредненными (макроскопическими) полями. Вектор Пойнтинга в макроскопической среде может быть определен самосогласованно с микроскопической теорией таким образом, что пространственно усредненный микроскопический вектор Пойнтинга точно предсказывается макроскопическим формализмом. Этот результат строго действителен в пределе малых потерь и позволяет однозначно идентифицировать форму вектора Пойнтинга в макроскопической электродинамике. ^[5

История

Общее представление о потоке механической энергии в пространстве впервые было введено Н. А. Умовым в 1874 году для упругих сред и вязких жидкостей. На этом основании в более старых русскоязычных публикациях вектор плотности потока энергии любой физической природы называется вектором Умова . В 1884 году Д. Г. Пойнтингом были разработаны представления о плотности потока электромагнитной энергии. Поэтому вектор плотности потока электромагнитной энергии называется вектором Пойнтинга.

Сами же законы сохранения и превращения энергии, где присутствует понятие плотности потока какого-либо вида энергии, используются, как правило, без указания имен первооткрывателей, поскольку законы сохранения являются следствием других уравнений и дополнительных условий.

Теорема Пойнтинга

Теорема Пойнтинга (англ. Об этом говорит сайт https://intellect.icu . Poynting's theorem) — теорема, описывающая закон сохранения энергии электромагнитного поля. Теорема была доказана в 1884 Джоном Генри Пойнтингом. Все сводится к следующей формуле:

где — плотность энергии: ;

— электрическая постоянная, — магнитная постоянная;

— оператор набла; S — вектор Пойнтинга;

J — плотность тока и E — напряженность электрического поля.

Теорема Пойнтинга в интегральной форме:

,

где — поверхность, ограничивающая объем .

В технической литературе теорема обычно записывается так ( — плотности энергии):

,

где — плотность энергии электрического поля, — плотность энергии магнитного поля и — мощность джоулевых потерь в единице объема.

Вывод теоремы пойнтинга

Теорема может быть выведена с помощью двух уравнений Максвелла (для простоты считаем, что среда - вакуум (μ=1, ε=1); для общего случая с произвольной средой, нужно в формулы к каждому ε₀ и μ₀ приписать ε и μ):

Домножив обе части уравнения на , получим:

Рассмотрим сначала уравнение Максвелла-Ампера:

Домножив обе части уравнения на , получим:

Вычитая первое из второго, получим:

Наконец:

Поскольку вектор Пойнтинга определяется как:

это равносильно:

Обобщение Теоремы Пойнтинга

Механическая энергия описанной выше теоремы

где u_m — кинетическая энергия плотности в системе. Она может быть описана как сумма кинетической энергии частиц α

— поток энергии, или «механический вектор Пойнтинга»:

Уравнение непрерывности энергии или закон сохранения энергии

Альтернативные формы Теоремы Пойнтинга

Можно получить и другие формы теоремы Пойнтинга. Вместо того чтобы использовать вектор потока можно выбрать форму Авраама , форму Минковского , или какую-либо другую.

Распространение электромагнитной энергии

Связь между конфигурацией полей и вектором Умова существует и в случае переменных полей, когда электрическое и магнитное поля изменяются во времени. По прежнему в каждый данный момент вектор Умова направлен перпендикулярно векторам напряженности электрического и магнитного полей (по правилу буравчика), а его абсолютная величина пропорциональна произведению абсолютных величин напряженности полей.

Если длина двухпроводной линии мала по сравнению с длиной волны питающего ее переменного тока, то картина распространения энергии мало отличается от картины распространения энергии при постоянном токе.

При малой длине линии за время, в течение которого электрическое поле пробегает от начала до конца линии, напряжение в ее начале почти не успевает измениться. Поэтому в каждый данный момент напряжение между проводами по всей длине линии получается примерно одинаковым.

Когда источник и нагрузка не обладают реактивным- сопротивлением, напряжение и ток в линии совпадают по фазе, а значит электрическое и магнитное поля вокруг линии также изменяются в одинаковой фазе.

В этом случае векторы Е и Н одновременно проходят через нуль и меняют свое1 направление в пространстве на обратное, следовательно, вектор Умова не изменяет своего направления в пространстве.



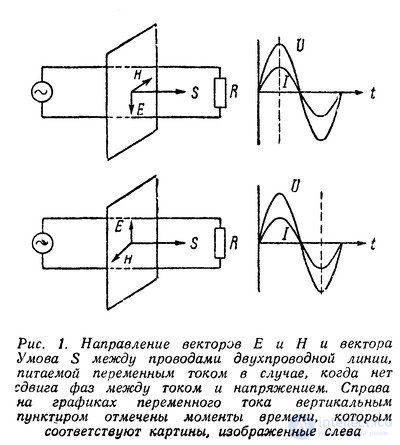
Две мгновенных картины, соответствующие двум разным направлениям векторов Е и Н, изображены на рис. 1.

Таким образом, несмотря на то, что электрическое и магнитное поля изменяют свое направление в пространстве дважды за период, энергия все время течет в одну сторону от источника ЭДС к нагрузке так же, как и в случае постоянного тока.

Разница заключается только в том, что при постоянном токе вектор Умова остается во времени постоянным как по величине, так и по направлению (так же, как и векторы Е и Н), а при переменном токе вектор Умова периодически изменяется по величине, дважды за период достигая максимума и падая до нуля (так же, как и произведение абсолютных величин векторов Е и Н), но не изменяя своего направления в пространстве.

Это значит, что в то время как при постоянном токе поток энергии вдоль линии не изменяется со временем, в случае переменного тока он пульсирует во времени.

Иная картина получится в том случае, когда есть сдвиг фаз между напряжением и током в линии и, следовательно, изменения электрического и магнитного полей сдвинуты по фазе. Это происходит тогда, когда нагрузка или источник ЭДС обладают не только активным, но и реактивным сопротивлением.

Рассмотрим сначала воображаемый случай, когда нагрузка представляет собой чисто реактивное сопротивление, а источник и линия не обладают активными сопротивлениями. Тогда сдвиг фаз между напряжением и током в линии будет равен 90° и изменения векторов Е и Н будут происходить с таким же сдвигом фаз.

При этом изменения направлений векторов Е и Н будут происходить не одновременно, а со сдвигом во времени в четверть периода. Но всякий раз, когда меняет направление на обратное только вектор Е или только вектор Н, вектор Умова тоже изменяет направление на обратное. Значит вектор Умова будет изменять свое направление за период четыре раза.

На рис. 2 изображены две мгновенные картины, соответствующие разным направлениям вектора Умова.



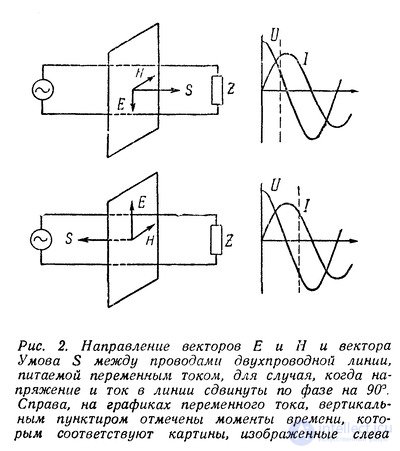
Вектор Умова будет, кроме того, изменяться и по величине в соответствии с изменением произведения абсолютных величин векторов Е и Н.

Продолжая такое же построение, как на рис. 2, для двух следующих четвертей периода, легко убедиться, что в течение первой и третьей четвертей периода поток энергии направлен от источника ЭДС к нагрузке, а в течение второй и четвертой четвертей — от нагрузки к источнику. При этом количество энергии, протекающей как в ту, так и в другую сторону, одинаково. Это значит, что поток энергии в среднем за период в любом сечении линии равен нулю.

Такой результат вполне согласуется с тем, что чисто реактивное сопротивление не потребляет энергии от источника. В течение четверти периода оно накапливает энергию, поступающую из источника, а в течение другой четверти периода возвращает источнику всю эту энергию.

В реальных случаях нагрузка, источник ЭДС и линия всегда обладают активным сопротивлением. Поэтому сдвиг фаз между напряжением и током в линии, а значит и между изменениями векторов Е и Н всегда меньше 90°. В этом случае вектор Умова по прежнему четыре раза за период меняет свое направление на обратное.

Но в отличие от предыдущего случая время, в течение которого он направлен в одну или в другую сторону, оказывается различным: в течение большего времени он направлен в ту сторону, которая соответствует одинаковым знакам Е и Н. (В этом нетрудно убедиться, произведя такие же построения, как на рис. 2, для случая, когда сдвиг фаз меньше 90°).

В этих условиях в обе стороны протекает уже не одинаковое, а различное количество энергии; от источника к нагрузке протекает больше энергии, чем обратно. В среднем за период энергия течет все же от источника к нагрузке,, хотя в некоторой части периода она течет от нагрузки к источнику. Это вполне согласуется с тем, что нагрузка, обладающая активным и реактивным сопротивлением, потребляет не всю энергию, полученную от источника за период, ибо часть энергии она возвращает назад источнику. Так как реальная линия обладает сопротивлением, то, как и в случае линии с постоянным током, появляется продольное электрическое поле. Вследствие этого силовые линии поля выгибаются вперед, векторы Умова отклоняются к проводам, а часть энергии втекает в провода, рассеиваясь в них в виде тепла.

Вау!! 😲 Ты еще не читал? Это зря!

• Электромагнитное поле
• магнитное поле
• Электрическое поле
• Напряженность поля

Исследование, описанное в статье про теоремы пойнтинга, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теоремы пойнтинга, вектор пойнтинга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Переменный электрический ток. Электромагнитное поле