Привет, Вы узнаете о том , что такое уравнение шредингера, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое уравнение шредингера , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.

Вот мы и подошли к настоящей квантовой механике. Все, что было до сих пор, — это интуитивные полуклассические представления, позволившие инкорпорировать в классическую физику идеи физики квантовой. Но этот уровень знаний недостаточен для расчетов, количественных предсказаний многих явлений. Требуется стройная система, теория движения (или распространения) микрочастиц с дуальными (волна-корпускула) свойствами.

4.1. Волна вероятности

Предыдущая закончилась констатацией, что мы пока не установили, что именно колеблется при движении электрона. В истории физики такое уже случалось. Когда-то при выводе уравнений электродинамики Максвелл тоже не знал, что представляют собой описываемые им колебания и волны, но уравнения оказались верны. Поэтому отложим пока вопрос о физической природе волн де Бройля и просто введем некую «электронную» волну, то есть волновую функцию 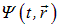. О ней мы знаем пока только одно: волновая функция должна описывать результаты опытов, доказывающих волновые свойства электронов (дифракцию и т. п.).

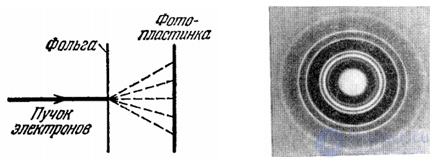
Рис. 4.1. Дифракционная картина при прохождении электронного пучка через металлическую фольгу

Видео 4.1. Дифракция электронов на поликристалле.

Представим мысленно эксперимент В.А. Фабриканта (см. разд. 3.2), в котором электроны поочередно направлялись на кристалл, играющий роль дифракционной решетки. За кристаллом помещалась фотопластинка, на которой в конце концов возникали типичные дифракционные кольца. Из классической физики известно, какие математические средства описывают такую картину: обычное сложение интерферирующих волн, интенсивности которых пропорциональны

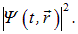
Правда, в отличие от обычной волны электрон не делится на части: при прохождении электронов через кристалл каждый из них попадает в какую-то одну точку на фотопластинке, вызывая почернение именно здесь и нигде больше. В этом проявляются свойства электрона как частицы. Несмотря на одинаковые начальные условия, электроны, как показал опыт, попадают в разные точки. О данном конкретном электроне заранее неизвестно, в какую именно точку на пластинке он попадет. В этом проявляются его волновые свойства. Дифракционная картина возникает, когда через кристалл пройдет достаточно много таких электронов. Интенсивность почернения пластинки в данной точке пропорциональна числу попавших туда частиц, то есть вероятности попадания.

В классической же физике почернение пластинки определяется интенсивностью волны, то есть квадратом модуля волновой функции. Выходит, что величина

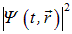
пропорциональна вероятности обнаружить электрон в окрестности точки 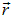в момент времени t. Волна де Бройля — это волна вероятности! Отдельный акт взаимодействия электрона с кристаллом остается отдельным актом (электрон-частица), но результат его можно предсказать только вероятностно, статистически (электрон-волна). В этом — смысл корпускулярно-волнового дуализма. Квантовая механика создана и 1925–1927 гг. В. Гейзенбергом и Э. Шредингером; вероятностная интерпретация волновой функции дана чуть позже в работах М. Борна и школы Н. Бора.

Рис. 4.2. В. Гейзенберг сформулировал принцип неопределенностей в 1927 г.

Рис. 4.3. Э́рвин Ру́дольф Йо́зеф Алекса́ндр Шредингер (1887–1961)

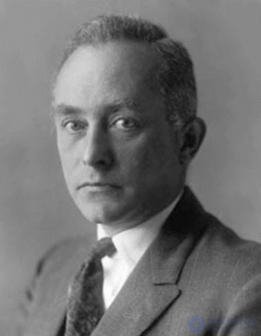
Рис. 4.4. Макс Борн (1882–1970)

Итак, вероятность найти электрон в окрестности точки 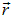должна быть пропорциональна

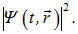
Но вероятность обнаружить электрон точно в данном месте исчезающе мала; имеет смысл говорить лишь о его попадании в малый объем 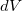окружающий эту точку. Ясно, что вероятность 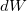обнаружить там электрон пропорциональна величине объема. Поэтому для вероятности имеем

Иными словами

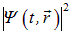
— это плотность вероятности найти частицу в точке с радиус-вектором .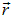

Вероятность 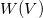найти частицу в каком-то конечном объеме 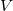вычисляется с теоремы помощью сложения вероятностей, то есть интегрированием

Интегрирование в (4.2) ведется по объему 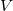(в случае одномерного движения — по отрезку).

Полная вероятность найти частицу хоть где-нибудь в пространстве должна быть равна единице. Отсюда — так называемое условие нормировки волновой функции: такой же интеграл по всему пространству равен единице, то есть

Замечание: выполнение этого условия возможно для тех задач, в которых классическая частица движется в ограниченной области пространства (финитное движение). Для инфинитных (неограниченных в пространстве) движений условие нормировки усложняется.

Наблюдаемые физические величины должны описываться действительными числами и функциями. Соответственно, мы представляли классические волны (звуковые, электромагнитные) в виде

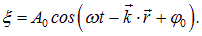
Можно было бы воспользоваться математическим формализмом комплексных чисел, основываясь на формуле Эйлера

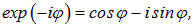
где

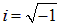
— мнимая единица. Тогда ту же волну можно было бы представить в виде действительной части выражения

где

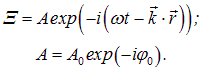
Рис. 4.5. Леона́рд Э́йлер (1707–1783)

Начальная фаза здесь включена в комплексную амплитуду А. В применении к классическим волнам оба формализма эквивалентны, так как в конечном итоге берется только действительная часть волны. В отличие от классических волн, волна вероятности комплексна. Физические наблюдаемые величины выражаются через квадрат модуля волновой функции, так что и в квантовой механике они будут описываться действительными числами. Но комплексность волновой функции имеет глубокую связь с законом сохранения электрического заряда, так что применение комплексных чисел и функций в квантовой механике — не прихоть, а необходимость. Поверхность постоянной фазы в волне 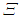(4.4) распространяется вдоль волнового вектора 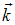, фазовая скорость волны по-прежнему равна

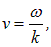
так что переход к комплексным волнам не меняет привычных нам соотношений.

4.2. Общее уравнение шредингера

Волновая функция является главным объектом изучения в квантовой механике. Говоря о каком-то состоянии в классической физике, мы подразумевали, что в момент времени t=0 частица имела некие положение и скорость (импульс), а дальнейшая ее судьба предопределена уравнениями движения Ньютона.

Состояние в квантовой механике имеет иной смысл: в момент времени 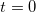задана волновая функция, изменение которой регулируется пока не известным нам уравнением (Шредингера). В этом смысле теперь понимается причинность: в классике — точные предсказания положений и скоростей, в квантовой механике — предсказания состояний (волновых функций). Уравнения новой физики (в данном случае — уравнение Шредингера) никогда не выводятся логически из прежних принципов (иначе это будет не новая теория, а следствие старой). Но квантово-механическое уравнение должно иметь некие классические корни, поскольку классическая механика хороша в области своей применимости. Далее мы приведем не вывод, но наводящие соображения (как в разд. 3.3 для соотношений неопределенностей).

Свободной частице соответствует волна де Бройля, которую мы записываем в виде классической плоской волны (в комплексной форме)

где модуль волнового вектора k связан с длиной волны соотношением

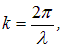
C — амплитуда. Мы использовали уже известную связь энергии и импульса частицы с частотой и длиной волны де Бройля. Искомое уравнение для волновой функции не должно содержать 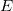и 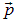так как это — характеристики конкретного состояния частицы. Попробуем найти операции над волновой функцией свободной частицы, позволяющие исключить параметры 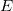и 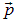Е и р. Имеем для производной по времени

и по пространственной координате

Такие же уравнения возникнут при дифференцировании по , 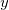и . Повторяя дифференцирование по координатам, получаем

Складывая (4.8) с аналогичными уравнениями для вторых производных по , 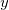и , приходим к соотношению

где знаком 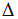обозначен оператор Лапласа:

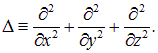
Рис. 4.6. Пьер-Симо́н Лапла́с (1749–1827)

В этом месте возникает различие между релятивистским и нерелятивистским случаями. Рассматриваемая здесь квантовая механика — нерелятивистская теория, в которой

Это классическое coотношение позволяет связать дифференцирование по времени в (4.6) с дифференцированием по пространственным координатам в (4.9) и тем самым исключить из уравнения зависимость от энергии и импульса частицы:

Это уравнение вполне бы нас устроило, но написано оно пока только для свободной частицы. Легко понять, как должно выглядеть уравнение для системы с постоянным значением 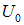потенциальной энергии. Полная энергия равна сумме

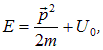
так что получаем

В случае частицы, находящейся в произвольном потенциальном поле, вблизи точки 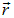потенциальную энергию можно считать постоянной величиной 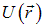, так что искомое обобщение почти с очевидностью следует из уравнения (4.11):

Это и есть основное уравнение квантовой механики — знаменитое общее уравнение Шредингера. Подчеркнем еще раз, что вывести его строго невозможно, но можно угадать, исходя из наводящих соображений. Соответствие уравнения и его следствий физической реальности проверяется экспериментально. Уравнение Шредингера по сути есть аналог классического соотношения между полной энергией 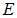частицы и ее кинетической энергией 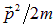. Для свободной частицы они совпадают. При наличии потенциального поля это соотношение принимает вид

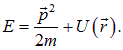
Мы уже знаем, что полной энергии соответствует производная по 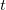, компонентам импульса — производные по x,y,z, а кинетической энергии — вторые производные по пространственным координатам, поскольку импульс входит в нее во второй степени. Классической потенциальной энергии, как мы видим, в квантовой механике соответствует обычное произведение 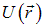на волновую функцию.

Уравнение Шредингера линейно по искомой волновой функции, откуда сразу же вытекают следствия:

Если — решение уравнения (4.12), то — также его решение при любой константе СА. Следовательно, подбором постоянной А можно добиться выполнения условия нормировки (4.3). Если и — решения уравнения Шредингера, то линейная комбинация — также его решение (принцип суперпозиции, то есть основа явления интерференции).

4.3. Операторы, симметрия и законы сохранения

Итак, состояние электрона описывается в квантовой механике волновой функцией 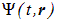. Но куда подевались координаты, импульс и прочие величины, известные из классической теории? От классических представлений придется отказаться. Взамен у нас появились так называемые операторы, то есть некие операции, совершаемые над 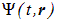. Из уравнения Шредингера видно, что оно воспроизводит связь

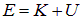
полной энергии с кинетической 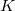и потенциальной 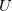, но классические величины заменены на операторы, действующие на волновую функцию 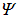. Будем обозначать оператор тем же символом, что и классическую величину, снабжая его для отличия «шляпкой». Тогда уравнение Шредингера (4.12) можно записать в операторной форме, в которой отчетливо видна его связь с энергетическими соотношениями классической физики:

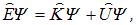
где введены операторы

Здесь

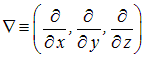
оператор градиента, квадрат которого дает оператор Лапласа 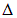. Оператор радиус-вектора 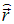сводится к простому умножению 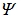на вектор 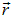; то же справедливо для любой функции 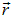(в частности, для потенциальной энергии).

Мы пришли к способу перехода от известных классических соотношений к соответствующим им квантовым: необходимо классические величины заменить в них соответствующими им операторами.

Правило 1

При этом энергии частицы

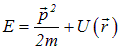
в потенциальном поле соответствует оператор полной энергии

В этих обозначениях уравнение Шредингера (4.12) имеет вид

Оператор полной энергии называется гамильтонианом (аналог функции Гамильтона в теоретической механике).

Рис. 4.7. Сэр Уи́льям Ро́уэн Га́мильтон (1805–1865)

Напомним, что в классической механике законы сохранения связаны с симметрией системы: энергия - с трансляцией (сдвигом) времени

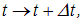
импульс — с трансляцией пространства

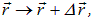
момент импульса — с поворотами в пространстве (трансляцией углов)

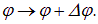
Трансляцию какой-то обобщенной координаты 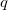производит оператор дифференцирования по этой координате. Например, для бесконечно малой трансляции

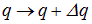
имеем по определению производной

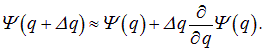
Поэтому не случайно в квантовой механике полной энергии соответствует операция взятия производной по времени

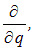
а импульсу — градиент. Аналогично оператор проекции момента импульса на какую-то ось пропорционален оператору дифференцирования

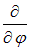
по углу поворота вокруг этой оси:

(4.16) 4.4. Стационарное уравнение Шредингера В теории операторов важную роль играют так называемые собственные состояния операторов. Это такие состояния, которые при действии данного оператора меняются тривиальным образом: умножаются на некоторое число. Это число называется собственным значением оператора, соответствующим данному собственному состоянию. Чтобы найти собственные состояния и собственные значения какого-то оператора, надо решить уравнение где индекс n отличает одно решение от другого. Набор величин , то есть набор собственных значений оператора, определяет его свойства. Рассмотрим в качестве примера операцию поворота вокруг некоторой оси .Роль состояний играют здесь обычные радиусы-векторы. Очевидно, что при повороте все векторы меняются, кроме параллельных оси. Это и есть собственные векторы оператора поворота вокруг оси , причем соответствующее собственное значение равно единице. Аналогичны выводы для поворота вокруг осей и . Произвольный поворот можно получить комбинацией этих трех поворотов. Соответственно, любой радиус-вектор можно представить как линейную комбинацию трех собственных векторов . Ситуация с другими операторами по сути ничем не отличается от описанной: зная набор собственных состояний , любое другое состояние можно получить с помощью линейной комбинации, то есть с помощью принципа суперпозиции: (4.17) Связь математики с физикой реализуется в следующем правиле. Правило 2

продолжение следует...

Продолжение:

Часть 1 4. Уравнение Шредингера
Часть 2 4.5. Уравнение Шредингера для простейших систем - 4. Уравнение Шредингера
Часть 3 4.7. Отражение и туннелирование частиц - 4. Уравнение Шредингера
Часть 4 - 4. Уравнение Шредингера