Лекция
Это продолжение увлекательной статьи про уравнение шредингера.
...
style="color: rgb(0, 0, 0); font-family: Tahoma, Helvetica, sans-serif; font-size: 15px;">
|
Измерение некой физической величины всегда дает лишь одно из собственных значений Вероятность получить при измерении именно n-ое собственное значение |
Следствие: в собственном состоянии  измерение
измерение  с вероятностью 100 % даст значение
с вероятностью 100 % даст значение 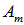 (так как в разложении (4.17) отличен от нуля лишь коэффициент с номером
(так как в разложении (4.17) отличен от нуля лишь коэффициент с номером  ).
).
Поскольку среди всех физических величин особую роль играет энергия, найдем уравнение для собственных состояний 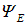 оператора полной энергии. Уравнение, согласно сказанному, имеет вид
оператора полной энергии. Уравнение, согласно сказанному, имеет вид

откуда следует решение
|
|
|
(4.18) |
Мы получили общий вид состояния, в котором энергия имеет определенное значение. Такие состояния называются стационарными. Естественно, пока невозможно сказать, чему равна энергия стационарного состояния, поскольку мы еще не указали рассматриваемую физическую систему. В уравнении (4.18) стоит некая функция 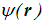 , не зависящая уже от времени. Она называется волновой функцией стационарного состояния. Зависимость стационарных состоянии от времени особенно проста — такая же как для свободной частицы. Отсюда следует, что в стационарном состоянии плотность вероятности не зависит от времени. В этом смысле и следует понимать название «стационарное». Подставляя решение (4.18) в общее уравнение Шредингера (4.12), получим стационарное уравнение Шредингера, то есть уравнение для
, не зависящая уже от времени. Она называется волновой функцией стационарного состояния. Зависимость стационарных состоянии от времени особенно проста — такая же как для свободной частицы. Отсюда следует, что в стационарном состоянии плотность вероятности не зависит от времени. В этом смысле и следует понимать название «стационарное». Подставляя решение (4.18) в общее уравнение Шредингера (4.12), получим стационарное уравнение Шредингера, то есть уравнение для 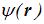 :
:
|
|
|
(4.19) |
Подчеркнем: это — уравнение для состояний с определенной энергией  . Об этом говорит сайт https://intellect.icu . В операторных обозначениях оно имеет вид
. Об этом говорит сайт https://intellect.icu . В операторных обозначениях оно имеет вид
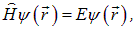
то есть представляет собой уравнение для собственных состояний гамильтониана. Задавая тот или иной вид потенциальной энергии, мы конкретизируем систему и получаем стационарное уравнение Шредингера, решения которого и описывают квантовые свойства системы.
Не следует думать, что система может быть только в стационарном состоянии. Возьмем характерный пример: пусть
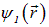
и

— два неких стационарных состояния какой-то системы с разными энергиями 
 1 и
1 и 
 2. Предположим, что в начальный момент времени волновая функция системы является симметричной суперпозицией этих состояний:
2. Предположим, что в начальный момент времени волновая функция системы является симметричной суперпозицией этих состояний:

Вопрос: что будет с системой в произвольный момент t.
Зная, что справедлив принцип суперпозиции и что зависимость собственных состояний от времени определяются соотношениями типа (4.18), можно сразу же написать волновую функцию:
|
|
|
(4.20) |
Плотность вероятности такого состояния зависит от времени! Введем обозначения для средней энергии

и частоты перехода
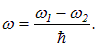
Тогда

и легко получаем вместо (4.20)
|
|
|
(4.21) |
Видно, что в момент t = 0 система находится в симметричном состоянии, к моменту времени  она перейдет в антисимметричное состояние, а в момент
она перейдет в антисимметричное состояние, а в момент 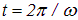 — снова вернется в симметричное состояние. Следовательно, система осциллирует между симметричным и антисимметричным состояниями с круговой частотой
— снова вернется в симметричное состояние. Следовательно, система осциллирует между симметричным и антисимметричным состояниями с круговой частотой 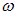 . Здесь усматривается аналогия с классической физикой: в рассмотренной ранее системе связанных осцилляторов возникают похожие собственные колебания (нормальные моды) и биения.
. Здесь усматривается аналогия с классической физикой: в рассмотренной ранее системе связанных осцилляторов возникают похожие собственные колебания (нормальные моды) и биения.
Свободная частица, движущаяся вдоль оси х
Потенциальная энергия равна нулю: 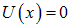 , и производные по y и z в операторе Лапласа исчезают. Уравнение (4.19) принимает вид
, и производные по y и z в операторе Лапласа исчезают. Уравнение (4.19) принимает вид
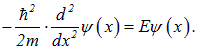
Введем волновой вектор  , обозначив
, обозначив

и перепишем уравнение в виде
|
|
|
(4.22) |
Существуют, как известно, два линейно независимых решения уравнения (4.22), так что общее решение есть суперпозиция двух волн — или стоячих:
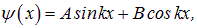
или бегущих:
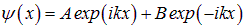
(первый член — волна бежит направо, второй — налево; постоянные  и
и 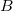 произвольны). Аналогия: такие же решения описывают колебания свободной струны. Поскольку возможны волны с произвольным значением волнового числа
произвольны). Аналогия: такие же решения описывают колебания свободной струны. Поскольку возможны волны с произвольным значением волнового числа  , энергия частицы (
, энергия частицы ( ) также может принимать любые значения, то есть, в данном случае свободного инфинитного движения — не квантуется. Для частицы, движущейся в произвольном направлении вдоль произвольно направленного волнового вектора
) также может принимать любые значения, то есть, в данном случае свободного инфинитного движения — не квантуется. Для частицы, движущейся в произвольном направлении вдоль произвольно направленного волнового вектора  , справедливы те же решения при замене
, справедливы те же решения при замене
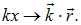
При решении большинства задач квантовой механики следует обратить внимание на то, что волновая функция всегда должна быть непрерывной — вероятность пребывания частицы не может меняться скачком от точки к точке. Кроме того, если потенциальная энергия непрерывна или имеет скачки, но только первого рода (конечные скачки) и не имеет бесконечных скачков (скачков второго рода), то из уравнения Шредингера следует, что и первая производная волновой функции также непрерывна.
Частица в бесконечно глубокой потенциальной яме
Потенциальная энергия в этой задаче имеет вид
|
|
|
(4.23) |
Такая система соответствует частице, движущейся вдоль прямой линии и отскакивающей от абсолютно отражающих препятствий в точках  и
и 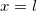 . В область бесконечного потенциала частица проникнуть не может, следовательно,
. В область бесконечного потенциала частица проникнуть не может, следовательно,  за пределами отрезка
за пределами отрезка  . Внутри ямы
. Внутри ямы  , и стационарное уравнение Шредингера имеет тот же вид, как для свободной частицы. Получатся те же решения в виде суперпозиции стоячих (или бегущих) волн, но в отличие от предыдущего случая добавятся граничные условия. Именно, в точках
, и стационарное уравнение Шредингера имеет тот же вид, как для свободной частицы. Получатся те же решения в виде суперпозиции стоячих (или бегущих) волн, но в отличие от предыдущего случая добавятся граничные условия. Именно, в точках  и
и 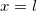 волновая функция должна обращаться в нуль (поскольку она непрерывна и равна нулю вне ямы). В классической механике точно такие граничные условия имеет уравнение для струны с закрепленными концами.
волновая функция должна обращаться в нуль (поскольку она непрерывна и равна нулю вне ямы). В классической механике точно такие граничные условия имеет уравнение для струны с закрепленными концами.
Общее решение имеет вид

Используем сначала первое граничное условие

Мы получили, что решение уравнения Шредингера должно иметь вид

Если продолжить нашу аналогию, то можно сказать, что на струне, закрепленной в одной точке, бегущих волн не бывает: отражение от неподвижной точки обязательно порождает стоячую волну. Однако на длину волны никаких ограничений не накладывается.
Теперь наложим второе из граничных условий:

Здесь есть два типа решений. При  получаем
получаем
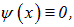
что означает отсутствие частицы в яме (вероятность найти ее всюду равна нулю). Поэтому нас интересует второе – нетривиальное – решение, когда

Это возможно лишь при некоторых значениях волнового вектора:

Так как энергия частицы связана с волновым вектором, то
|
|
|
(4.24) |
Мы получили квантование энергии, то есть наша «струна», закрепленная с обеих сторон, зазвучала, так как появились выделенные частоты.
Подставляя найденные разрешенные значения волнового вектора в выражение для волновой функции, получаем ее в виде
|
|
|
(4.25) |
Смысл квантового числа: оно на единицу больше числа нулей волновой функции. Значение постоянной
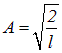
определяется из условия нормировки.
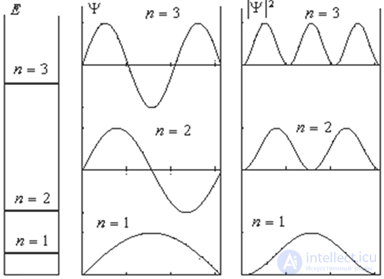
Рис. 4.8. Уровни энергии, волновые функции и распределение плотности вероятностей по координате x
Отметим, что значения 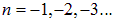 , при которых граничное условие в точке
, при которых граничное условие в точке 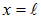 также будет выполнено, новых состояний не дают. Это видно и из выражения для энергии (4.24), в которое n входит в квадрате, и из выражения для волновой функции (4.25): изменение знака n приведет лишь к изменению знака волновой функции
также будет выполнено, новых состояний не дают. Это видно и из выражения для энергии (4.24), в которое n входит в квадрате, и из выражения для волновой функции (4.25): изменение знака n приведет лишь к изменению знака волновой функции 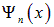 , что оставит неизменным распределение вероятностей
, что оставит неизменным распределение вероятностей  .
.
Откуда же берется дискретность уровней энергии, характерная и для атома? Сравним со свободной частицей: уравнения те же, но с иными граничными условиями! Здесь возможны две постановки задачи. В первом случае исследуется состояние, которому в классической механике соответствовало бы инфинитное движение (задача рассеяния). Обычно в таких случаях решения возможны при любых значениях энергии (как говорят, спектр непрерывен). Во втором случае исследуется состояние, которому в классике соответствует финитное движение в ограниченной области пространства (задача на связанные состояния). Требование конечности волновой функции во всем пространстве ведет к квантованию энергии. Подчеркнем: в этом случае стационарное уравнение имеет физически приемлемые решения не всегда, а лишь при некоторых значениях энергии  . Как следствие возникает дискретный спектр энергии системы.
. Как следствие возникает дискретный спектр энергии системы.
Пример. Определим разность соседних уровней энергии 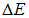 для частицы в бесконечно глубокой потенциальной яме при больших значениях n. Полученный результат используем для оценки разности энергий соседних уровней энергии поступательного движения молекул азота при комнатной температуре
для частицы в бесконечно глубокой потенциальной яме при больших значениях n. Полученный результат используем для оценки разности энергий соседних уровней энергии поступательного движения молекул азота при комнатной температуре 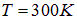 в сосуде. Примем массу молекулы
в сосуде. Примем массу молекулы  , а линейный размер сосуда
, а линейный размер сосуда  . Сравним полученный результат с кинетической энергией поступательного движения молекул азота.
. Сравним полученный результат с кинетической энергией поступательного движения молекул азота.
Используя выражение (4.24) для уровней энергии частицы в потенциальной яме, находим разность энергий соседних уровней
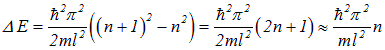
при больших значениях  . Средняя кинетическая энергия поступательного движения молекул азота равна
. Средняя кинетическая энергия поступательного движения молекул азота равна

Приравнивая  выражению (4.24) для энергии уровней частицы в яме, находим, что такая энергия соответствует квантовым числам порядка
выражению (4.24) для энергии уровней частицы в яме, находим, что такая энергия соответствует квантовым числам порядка
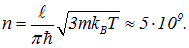
Уже само по себе это число говорит о том, что в области крайне высоких возбуждений работают классические формулы. Разность энергий соседних уровней получается, подстановкой в формулу для  найденного выражения для квантового числа:
найденного выражения для квантового числа:

В электрон-вольтах те же характеристики имеют значения

Относительная разность энергий соседних уровней ничтожно мала:
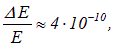
и потому в классическом пределе квантовой дискретностью пренебрегают.
Частица в трехмерной потенциальной яме
Это обобщение предыдущей задачи. Частица может двигаться в кубическом объеме с длиной ребра  . Нетрудно убедиться, что общее решение для волновой функции представимо в виде произведения одномерных волновых функций, полученных в предыдущей задаче:
. Нетрудно убедиться, что общее решение для волновой функции представимо в виде произведения одномерных волновых функций, полученных в предыдущей задаче:
|
|
|
(4.26) |
Такая волновая функция соответствует очевидному факту, что движения вдоль трех осей не зависят друг от друга, и каждое описывается прежними одномерными волновыми функциями. Энергия, как легко догадаться, будет равна сумме энергий движения по осям x, y, z:
|
|
|
(4.27) |

Рис. 4.9. Трехмерная потенциальная яма
Состояние системы теперь определяется тремя квантовыми числами  1,
1,  2 и
2 и  3, принимающими, как и прежде; целые значения. Здесь мы впервые сталкиваемся с важным понятием вырождения энергетических уровней, то есть с ситуацией, когда разные состояния системы имеют одинаковую энергию. В самом деле, минимальная энергия системы достигается при минимальных значениях всех квантовых чисел, то есть при
3, принимающими, как и прежде; целые значения. Здесь мы впервые сталкиваемся с важным понятием вырождения энергетических уровней, то есть с ситуацией, когда разные состояния системы имеют одинаковую энергию. В самом деле, минимальная энергия системы достигается при минимальных значениях всех квантовых чисел, то есть при  1,
1,  2,
2,  3. Эта энергия равна
3. Эта энергия равна

и ей соответствует одна волновая функция 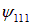 . Говорят, что основное состояние не вырождено (невырожденность состояния с минимальной энергией — общее правило). Первое возбужденное состояние получается, когда одно из квантовых чисел равно 2, а остальные по-прежнему равны единице; энергия его
. Говорят, что основное состояние не вырождено (невырожденность состояния с минимальной энергией — общее правило). Первое возбужденное состояние получается, когда одно из квантовых чисел равно 2, а остальные по-прежнему равны единице; энергия его
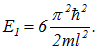
Но такую энергию имеют теперь три состояния с волновыми функциями  ,
, 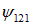 , и
, и  (квантовое число 2 можно выбрать тремя способами), поэтому говорят, что кратность вырождения первого возбужденного уровня равна трем (g = 3). Естественно, в другой системе может быть совершенно иная кратность вырождения (или отсутствие такового). Последующие состояния частицы в трехмерной потенциальной яме с бесконечными стенками также вырождены. Ясно, что вырождение уровней связано с симметрией системы, с равноправием всех осей. Если бы размеры ямы были разными
(квантовое число 2 можно выбрать тремя способами), поэтому говорят, что кратность вырождения первого возбужденного уровня равна трем (g = 3). Естественно, в другой системе может быть совершенно иная кратность вырождения (или отсутствие такового). Последующие состояния частицы в трехмерной потенциальной яме с бесконечными стенками также вырождены. Ясно, что вырождение уровней связано с симметрией системы, с равноправием всех осей. Если бы размеры ямы были разными  1,
1,  2,
2,  3 то всем трем направлениям, то для энергии мы бы получили вместо (4.27) выражение
3 то всем трем направлениям, то для энергии мы бы получили вместо (4.27) выражение
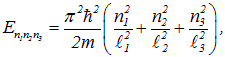
и вырождение могло бы иметь место лишь при определенных соотношениях между длиной, шириной и высотой потенциального ящика.
Одномерный осциллятор
В классической физике пружинный маятник (одномерный осциллятор) представляет собой точечное тело массой m, прикрепленное к пружине и колеблющееся с круговой частотой 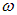 . Потенциальная энергия такой системы описывается выражением
. Потенциальная энергия такой системы описывается выражением

так что уравнение Шредингера записывается в виде

Отсюда можно найти решение для волновой функции основного состояния

Подставляя это выражение в уравнение Шредингера, легко убедиться, что энергия основного состояния равна

Мы не выписываем волновые функции возбужденных состояний осциллятора, но выражение для разрешенных значений энергии имеет вид ( — колебательное квантовое число)
— колебательное квантовое число)
|
|
|
(4.28) |
Здесь воспроизводится формула Планка и нулевые колебания
 ,
,
полученные ранее из соотношения неопределенностей (см. разд. 3.3).

Рис. 4.10. Уровни энергии и распределения плотности вероятностей по координате x для разных значений колебательного квантового числа. График потенциальной энергии осциллятора показан синей линией
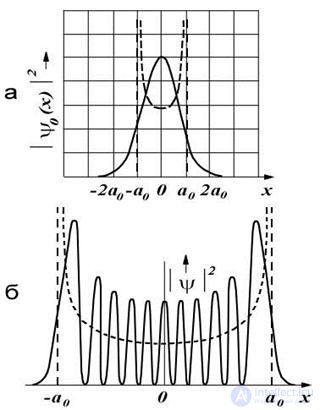
Рис. 4.11. Распределения вероятностей для классического (пунктир) и квантового (сплошная линия) осцилляторов.
a) n = 1; б) большие значения n
Трехмерный осциллятор
Эта задача является обобщением предыдущей. Как и для трехмерной потенциальной ямы с бесконечно высокими стенками, волновая функция представляется в виде произведения волновых функций одномерных осцилляторов, колеблющихся независимо вдоль осей  ,
, ,
, . Так, волновая функция основного состояния имеет вид
. Так, волновая функция основного состояния имеет вид

а уровни энергии трехмерного осциллятора описываются формулой
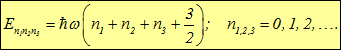
В отличие от одномерного осциллятора состояние определяется значениями трех квантовых чисел  1,
1,  2,
2,  3. Легко понять, что все возбужденные состояния должны быть вырожденными.
3. Легко понять, что все возбужденные состояния должны быть вырожденными.
Н. Бор на заре квантовой механики поставил вопрос о ее соотношении с классической. Обычные в нашем мире значения энергии велики по сравнению с характерной энергией основного состояния и расщеплением уровней: с высокой лестницы не различаем ступенек. Или, на языке квантовой механики: при больших квантовых числах (высоколежащих уровнях) должны воспроизводиться классические результаты. Покажем это на примере атома водорода.
В разд. 3.1 было получено классическое выражение для скорости электрона в атоме Бора на орбите радиусом R:

Отсюда легко получить классическую частоту вращения электрона
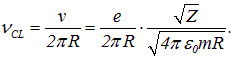
Кроме того, было найдено классическое выражение для энергии электрона на орбите

позволяющее выразить радиус орбиты через энергию электрона

Подставляя это выражение в формулу для классической частоты вращения  , получаем
, получаем
|
|
|
(4.29) |
Именно на этой частоте ожидается излучение электрона в классической теории.
Кроме того, в том же разделе было выведено выражение для энергии уровня с номером 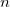 :
:

При 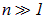
продолжение следует...
Часть 1 4. Уравнение Шредингера
Часть 2 4.5. Уравнение Шредингера для простейших систем - 4. Уравнение Шредингера
Часть 3 4.7. Отражение и туннелирование частиц - 4. Уравнение Шредингера
Часть 4 - 4. Уравнение Шредингера
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика