8. Физическая природа химической связи

Привет, Вы узнаете о том , что такое физика химической связи, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое физика химической связи , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.

Атомы представляют собой связанные электрическими силами системы ядер и электронов. В свою очередь, атомы под действием тех же сил в определенных условиях могут объединяться в молекулы. Первоначально химия предполагала существование специфических «химических сил» для объяснения образования молекул из атомов, а также химических реакций между атомами или молекулами. Однако таких «химических сил» не существует: образование молекул обусловлено обычными электрическими (кулоновскими) силами взаимодействия между заряженными частицами, то есть электронами и ядрами, из которых состоят атомы. Но механизм образования молекул можно понять только на основе квантовой механики.

8.1. Молекулы в контексте физики

Для простоты ограничимся рассмотрением простейших двухатомных молекул. Силы, удерживающие атомы в молекуле, вызваны взаимодействием внешних электронов, а электроны внутренних оболочек при объединении атомов в молекулы остаются в прежних состояниях. Различают два вида связи между атомами в молекуле: ионную (гетерополярную) и ковалентную (гомеополярную).

Ионная связь. Этот вид химической связи обусловлен переносом валентных электронов с одного атома на другой и кулоновским притяжением образовавшихся ионов. Иными словами, ионная связь осуществляется в том случае, когда электроны в молекуле можно разделить на две группы, каждая из которых все время находится около одного из ядер.

Электроны разделяются так, что около одного из ядер образуется избыток электронов, а около другого — их недостаток, то есть молекулу можно представить как образование, состоящее из отрицательного и положительного ионов, притягивающихся друг к другу (например, молекула 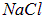состоит из ионов и ).

Для описания ионных молекул еще до создания квантовой механики с успехом применялись полуэмпирические способы расчета энергии связи, основанные на классической электростатике. Пусть, например, мы имеем дело с молекулами типа , и т. п. В начальном состоянии имеем два нейтральных атома, например и 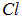, разнесенные на бесконечно большое расстояние. Попытаемся мысленно построить из них молекулу. Затрачивая энергию 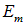, численно равную потенциалу ионизации щелочного металла, мы отрываем электрон от металла и переносим его на галоген. При присоединении электрона к последнему выделится энергия 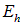(сродство галогена к электрону), так что энерговыделение на этом этапе составляет . Далее сближаем образованные нами ионы до равновесного расстояния 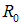(размер молекулы). При этом выделится дополнительная энергия кулоновского взаимодействия . Полная выделившаяся энергия и есть энергия связи получившейся молекулы: именно ее надо затратить, чтобы разорвать молекулу на составные части:

Учитывая, что кулоновская энергия равна

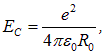
находим отсюда выражение для равновесного расстояния:

Применим полученную формулу для оценки размера молекулы 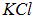. Берем экспериментальные данные: так что кулоновская энергия будет

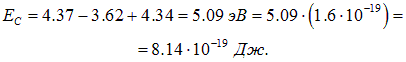
Отсюда легко находим размер молекулы

Получившаяся величина примерно в пять раз превышает радиус Бора и дает вполне приемлемую оценку размера молекулы. Отметим, что для равновесного межъядерного расстояния в молекуле 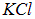эксперимент дает .

Оценим также размер молекулы другого соединения — , для которого 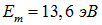и 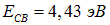. Чтобы не повторять аналогичных выкладок, используем уже полученный результат. Имеем в этом случае:

что в

раза больше кулоновской энергии для молекулы 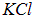. Соответственно, размер молекулы будет в такое же число раз меньшим:

(эксперимент для равновесного межъядерного расстояния дает значение ).

Отчуждение электрона одним ионом у другого (ионная связь) встречается в большинстве неорганических соединений, особенно в молекулах, состоящих из атомов далеких групп. Кроме соединений щелочных металлов и галогенов можно привести и другие примеры. Однако изложенные классические соображения не дают возможности вычислить независимо энергию связи молекулы (или ее размер). Само возникновение равновесного расстояния остается вне пределов компетенции такой теории. Силы электростатического притяжения между ионами должны уравновешиваться в равновесном состоянии какими-то силами отталкивания. Природа этих сил довольно сложна и связана с перекрытием электронных оболочек ионов. При сближении атомов оболочки начинают сильно деформироваться, что препятствует дальнейшему сближению. Величина — это равновесное расстояние между ионами, на котором силы электрического притяжения уравновешиваются квантово-механическим отталкиванием атомов на близких расстояниях.

Ковалентная связь. Второй вид связи наблюдается в молекулах, где электроны, осуществляющие связь, значительную часть времени проводят в пространстве между атомами и в какой-то мере являются «общими» для обоих ядер. Гомеополярная (ковалентная) связь характерна для большинства молекул с двумя одинаковыми атомами ( и т. д.). Гомеополярная связь не поддается классическому описанию, требует квантового рассмотрения.

Рассмотрим простейшую гомеополярную молекулу — молекулу водорода. Впервые это было сделано в 1927 г. В. Гайтлером и Ф. Лондоном. Мы ограничимся принципиальным анализом, опуская проведение расчетов, так как нашей задачей является уяснение физической природы ковалентной (гомеополярной) связи. Схема взаимодействий в такой молекуле, состоящей из двух протонов (ядер атома водорода) А и В и двух электронов 1 и 2, показана на рис. 8.1.

Рис. 8.1. Схема взаимодействия в молекуле водорода

Уравнение Шредингера для системы имеет вид

где через 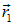и обозначены радиус-векторы первого и второго электронов, а — гамильтониан системы:

Гамильтониан содержит оператор кинетической энергии электрона 1 и потенциальную энергию того же электрона в кулоновском поле ядра А. Аналогичную структуру имеет гамильтониан 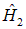. Оператор U описывает четыре взаимодействия: электрона 1 с ядром В, электрона 2 с ядром А, электронов между собой и ядер — также между собой. Ядра имеют массу, примерно в 2 000 раз превышающую массу электрона, поэтому они движутся гораздо медленнее электронов, и в первом приближении их можно считать неподвижными (такое приближение называется адиабатическим). Поэтому волновая функция

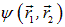
рассматривается как функция координат только электронов, а расстояние R между ядрами, важное в проблеме ковалентной связи, входит в волновую функцию как параметр. Получающиеся из уравнения Шредингера собственные значения энергии будут тогда зависеть от расстояния R, то есть

причем в случаях параллельной и антипараллельной ориентации спинов электронов характер этой зависимости оказывается различным.

Полная волновая функция зависит не только от пространственных координат электронов, но и от их спинов. Вследствие принципа Паули (согласно которому данный набор квантовых чисел может иметь лишь одна частица), такая полная волновая функция должна быть антисимметричной относительно перестановки электронов. Поскольку спиновое состояние не зависит от орбитального, пространственные и спиновые переменные разделяются, и полную волновую функцию электронов в молекуле водорода можно представить в виде произведения координатной и спиновой функций:

Из принципа Паули следуют свойства волновых функций:

Симметричная спиновая волновая функция соответствует параллельному расположению векторов спинов электронов, то есть суммарному спину электронов S = 1. Такое состояние называется триплетным по числу (2S + 1) = 3 возможных проекций суммарного спина. Во втором же случае антисимметричная спиновая функция связана с противоположно ориентированными спинами, дающими в сумме S = 0, и, следовательно, возможно только одно значение проекции полного спина, и состояние называется синглетным.

Взаимодействие между нейтральными атомами, когда расстояние между ядрами R много больше характерных размеров электронных оболочек, то есть радиуса Бора

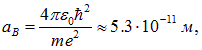
практически отсутствует, а энергия системы равна удвоенной энергии связи атома водорода , где

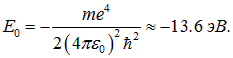
При уменьшении R до нуля эта энергия будет бесконечно возрастать из-за кулоновского отталкивания ядер.

Результаты расчетов можно описать следующим образом. Если спины электронов параллельны, то при сближении атомов водорода энергия системы монотонно увеличивается, никакого связанного состояния не возникает (кривая 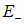на рис. 8.2).

Рис. 8.2. Зависимость энергии Е молекулы водорода от расстояния R между атомами:
на больших расстояниях существуют два нейтральных атома водорода с общей энергией ;
кривая Е_– соответствует триплетному состоянию электронов и проходит выше асимптотического значения
— связанного состояния молекулы в этом случае не существует; кривая соответствует синглетному
состоянию электронов, она имеет минимум при (конечный размер молекулы),
расстояние которого от асимптотического значения и есть энергия связи молекулы водорода

В этом случае предоставленные самим себе два атома вновь разойдутся, стремясь к состоянию с наименьшей возможной энергией. Условие существования связанного состояния — наличие минимума энергии системы при некотором значении 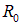— выполняется только при синглетном состоянии электронов, когда их спины антипараллельны (кривая 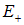на рис. 8.2).

Понять такое поведение энергии можно на качественном уровне, если рассмотреть два водородных атома, находящихся на большом расстоянии

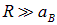
друг от друга. Тогда оператором взаимодействия U в гамильтониане (8.5) можно пренебречь, и мы имеем два независимых атома, описываемых суммой гамильтонианов 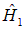и . Решения соответствующего каждому из них уравнения Шредингера мы уже знаем. Введем обозначения для получающихся волновых функций: и . Тогда решение для суммы гамильтонианов будет представляться в виде произведения волновых функций

а энергия — в виде суммы энергий, то есть будет равна 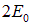. Физический смысл произведения волновых функций очевиден: электрон 1 находится в поле ядра А1, а электрон 2 — в поле ядра В2. Но электроны неразличимы, и эта физическая ситуация ничем не отличается от случая, когда электрон 2 находится в поле ядра 1А, а электрон 1 — в поле ядра В2. Этому соответствует иное произведение волновых функций:

которое тоже является решением уравнения Шредингера с той же энергией 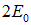. Об этом говорит сайт https://intellect.icu . Согласно принципу суперпозиции, решением с этой же энергией будет и любая линейная комбинация указанных произведений. Поскольку принцип Паули требует, чтобы полная волновая функция была либо симметрична, либо антисимметрична по пространственным координатам электрона, она должна иметь вид

где — вычисляемые нормировочные коэффициенты, обеспечивающие равенство единице полной вероятности:

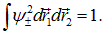
Подставляя сюда выражения (8.7) и учитывая, что и уже нормированы на единицу, получаем

откуда

Величина Р, называемая интегралом перекрытия, равна

Она характеризует степень перекрытия волновых функци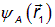й и , то есть степень независимости пространственного распределения электронов друг от друга, и играет важную роль в теоретических расчетах свойств молекул.

Если учесть теперь оператор взаимодействия U, то в зависимости от симметрии волновой функции получатся поправки к энергии разных знаков. В случае антисимметричного состояния (полный спин электронов S = 1) поправка получается положительной (отталкивание атомов), и связанного состояния не возникает. В случае же симметричного состояния (полный спин электронов S = 0) поправка для больших R отрицательна (притяжение атомов), что приводит к образованию молекулы водорода.

Осмыслить такое поведение поправки к энергии помогает график волновой функции. Ось z направим по линии, соединяющей ядра атомов водорода, а начало отсчета выберем в средней точке между ядрами, так что координаты ядра А равны (0, 0, –R/2), а ядра В — (0, 0, R/2). Для простоты рассмотрим волновые функции на этой оси, причем для случая симметричного расположения электронов относительно начала отсчета:

Тогда

Графики этих функций представлены на рис. 8.3.

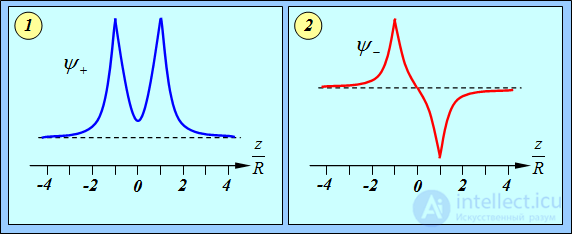
Рис. 8.3. Волновые функции электронов в молекуле водорода на оси, соединяющей ядра атомов,
для синглетного и триплетного состояний

Мы видим, что в обоих случаях существует наибольшая вероятность найти электроны вблизи ядер — волновые функции имеют экстремумы в точках

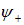Однако при сближении атомов в пространстве между ядрами происходит перераспределение плотности электронов, поведение которой различается в зависимости от типа симметрии пространственной части волновой функции — или . В состоянии электроны часть времени проводят в области между протонами (волновая функция в этой области заметно отлична от нуля). В центре между атомами получается электронное облачко, притягивающее к себе протоны — возникает стягивающее действие и образуется молекула. В состоянии же плотность электронов между протонами уменьшается (волновая функция проходит через нуль), отталкивание протонов не экранируется, что и приводит к увеличению энергии системы в этом состоянии (см. рис. 8.2). Положение минимума, таким образом, определяется из решения уравнения Шредингера с учетом потенциальной энергии электрического взаимодействия электронов и протонов в молекуле.

Численные результаты , для кривой , полученные в таком подходе, следует сравнить с экспериментальными данными: , . Разница в энергии связи составляет 31 %, в размере молекулы — 17 %.

Комбинации различных типов связи. Мы познакомились с двумя типами связи — ионной и ковалентной. В первой основную роль играет «перескок» электронов от одного атома к другому, во второй — дополнительные силы притяжения между атомами, порождаемые парой электронов с противоположными спинами. На самом деле оказывается, что такое резкое разделение не есть внутреннее свойство системы, но, скорее, недостаток наших методов расчета. Так, для улучшения согласия с экспериментом использованное приближение Гайтлера — Лондона может быть уточнено. Именно, ранее исходным моментом были волновые функции электронов — электрона 1 в поле ядра А и электрона 2 — в поле ядра В. Но электрон 1 также находится и в поле ядра В, а электрон 2 — в поле ядра А. Эти взаимодействия были учтены в поправочных членах, входящих в оператор U. Можно, однако, попытаться включить эти взаимодействия в рассмотрение с самого начала. Для этого представим волновую функцию первого электрона в виде

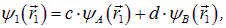
где c, d — некие численные коэффициенты. Они не являются независимыми: условие нормировки волновой функции y₁ приводит к связи между ними

где P — тот же интеграл перекрытия (8.10). Аналогичный вид имеет и волновая функция второго электрона:

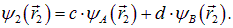
Волновую функцию синглетного двухэлектронного состояния строим как произведение

Мы видим, что здесь содержится волновая функция Гайтлера–Лондона — это последнее слагаемое в (8.13). Однако в приведенных формулах содержится и описание другого случая: это слагаемые

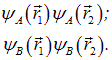
Физический смысл первого из них достаточно очевиден: оба электрона сосредоточены вокруг ядра А, образуя ион водорода Н ^–, в то время как ядро В, лишившееся электрона, образует ион Н ⁺. Мы видим, что этот случай описывает ионную связь. Второе слагаемое описывает аналогичную ситуацию, только ядра A и В меняются ролями. Для симметричной молекулы при обмене ядер местами ничего не меняется, откуда следует равенство коэффициентов

Таким образом, волновая функция (8.13) описывает некую комбинацию ионной и ковалентной связи, причем относительные веса этих двух типов связи одинаковы. Физически это, однако, не так, поскольку мы уже убедились, что метод Гайтлера–Лондона дает неплохое описание молекулы водорода. Но мы нащупали путь. Ясно, что недостаток метода Гайтлера–Лондона заключается в пренебрежении ионными членами, а недостаток только что изложенного подхода (его называют методом молекулярных орбит) — в переоценке влияния этих членов.

Можно принять оба этих метода как два различных исходных приближения, и естественным обобщением может стать улучшение численных значений коэффициентов в волновой функции, определяющих статистический вес ионной и ковалентной связей. Представим, например, симметричную волновую функцию как суперпозицию отдельных двухэлектронных состояний с произвольными коэффициентами :

При использовании такой волновой функции согласие с экспериментом заметно улучшается. В реальных расчетах коэффициенты определяются из условия минимума средней энергии, и их численные значения получаются автоматически, в зависимости от свойств системы. Если окажется, что численное значение одного из них намного превосходит по абсолютной величине два других, то можно говорить о преобладании связи определенного типа.

Так, если

то это будет ионная связь (электрон «перепрыгнул» с ядра В на ядро А).

Если

то это случай ионной связи (электрон перешел с ядра А на ядро В).

Если же, наконец,

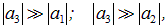
то мы имеем дело с ковалентной связью.

Этот подход применим как к молекулам из двух разных атомов, так и к соединениям одинаковых атомов, и позволяет учесть вклад ковалентного соединения в ионных молекулах и вклад ионной связи — в ковалентных молекулах. В применении к симметричным молекулам должно выполняться равенство

но третий коэффициент остается независимым, в отличие от метода молекулярных орбит. Сравнение экспериментов с расчетами по волновой функции (8.14) показало, что доля ионной связи в ковалентной молекуле атома водорода равна 20 %.

8.2. Пространственное строение молекул

В молекуле водорода химическая связь двух атомов осуществляется, как мы видели, за счет влияния электронных облаков между атомами. В невозбужденных атомах эти электроны находятся в s-состояниях, и их волновые функции сферически симметричны. Форма перекрывания этих облаков показана на рис. 8.4-1.

Рис. 8.4. Форма перекрывания электронных оболочек: 1 — оба электрона находятся в s-состоянии;
2 — один из электронов находится в р-состоянии

Но часто валентные электроны находятся в р-состоянии с угловым моментом, равным единице. В этом состоянии волновая функция, соответствующая нулевой проекции момента на какую-либо ось, пропорциональна косинусу угла q между этой осью и радиус-вектором. Следовательно, электронное облако имеет плотность, пропорциональную . Если изобразить такое облако на рисунке, то оно будет иметь форму восьмерки (точнее, тела, образованного вращением восьмерки вокруг продольной оси). Если такой р-электрон «спаривается» с s-электроном другого атома, то последний стремится «пристроиться» таким образом, чтобы перекрытие волновых функций было максимальным. Очевидно, что такая связь осуществляется в направлении вытянутости облака р-электрона (рис. 8.4-2).

Электронное облако в состоянии m = 0 «обволакивает» ось z, в двух других состояниях с проекциями 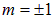такие же облака вытянуты по осям x и y. Это помогает уяснить пространственное строение молекул различных веществ. Ниже мы приводим некоторые характерные примеры.

Вода Н₂0. Атом кислорода имеет две заполненные оболочки: 1s и 2s, на которых размещаются четыре электрона. Оставшиеся четыре валентных электрона находятся на оболочке 2р. Их электронные облака отталкиваются и стремятся расположиться подальше друг от друга: три облака вытягиваются по осям и четвертому деваться некуда. Скажем, оно располагается по оси z, причем электрон имеет противоположный спин по сравнению с другим электроном, облако которого также расположено вдоль этой оси. Образуются спаренные электроны, не участвующие в химической связи. Для химической связи остаются свободными два электрона — облака по осям x и y. Атомы водорода, подсоединяясь, как было сказано, образуют молекулу треугольной формы (рис. 8.5), причем угол между направлениями на атомы водорода должен быть равен 90°.

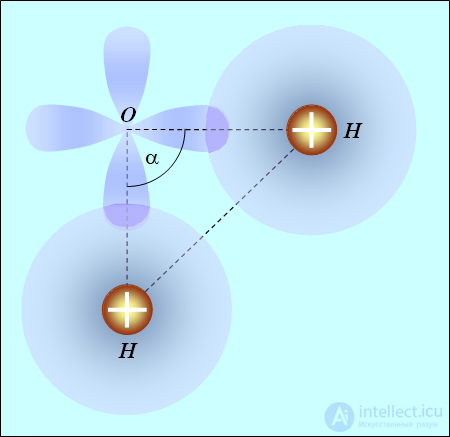
Рис. 8.5. Расположение атомов в молекуле воды

Но частично «оголенные» протоны также отталкиваются, и этот угол несколько возрастает: его экспериментальное значение . Это увеличение тем меньше, чем больше размер атома. Так, в аналогичном соединении атом серы больше атома кислорода, отталкивание протонов слабее и угол уменьшается до . Еще больше атом селена, и в молекуле 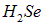атомы водорода расположены под углом .

Аммиак NH₃. Атом азота имеет конфигурацию . Как и в кислороде, четыре электрона, находящиеся в 1s и в 2s состояниях, спарены и не участвуют в химической связи. Остаются три p-электрона, и все три связи расположены по осям . При подсоединении трех атомов водорода образуется правильная треугольная пирамида с атомом азота в вершине (см. рис. 8.6).

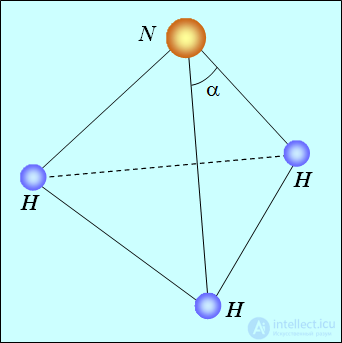
Рис. 8.6. Расположение атомов в молекуле аммиака

Из-за отталкивания протонов углы при вершине чуть больше . У похожего соединения, фосфина , угол ближе к прямому, а у . Из объемности молекулы аммиака следует существование двух вырожденных состояний, отличающихся положением атома азота по ту или иную сторону от основания пирамиды. Однако вырождение снимается вследствие квантовомеханического туннелирования, что ведет к расщеплению вырожденных уровней. Переходы между ними приводят к излучению, которое сделало возможным создание аммиачного мазера.

Перекись водорода . В случае, когда спариваются два p-электрона, максимальное перекрытие получается, если их «восьмерки» ориентированы вдоль одной оси. Таким образом, соединяются два атома кислорода в молекуле перекиси водорода (рис. 8.7).

Рис. 8.7. Форма и расположение электронных облаков в молекуле перекиси водорода

К ним подсоединяются обычным способом атомы водорода, причем вследствие отталкивания атомы водорода подсоединяются к кислородным облакам вдоль разных осей, так что линия ОО и две линии НО на рис. 8.7 все взаимно ортогональны (на самом деле валентный угол между ОО и ОН возрастает до ).

В некоторых молекулах связи между атомами осуществляются не одной, а двумя или тремя парами электронов (двойные или тройные связи). Пример тройной связи: молекула , которую химики записывают в виде

(черточка соответствует паре электронов). Тройная связь атома углерода имеет место в молекуле ацетилена:

Двойная связь атома углерода в молекуле этилена:

Квантовая механика объясняет эти и более сложные типы связей.

8.3. Молекулярные спектры

По сравнению с линейчатыми атомными спектрами молекулярные спектры имеют более сложную структуру. Они состоят из совокупности полос, которые, в свою очередь, распадаются на ряд тесно расположенных линий. Причина такого усложнения спектров заключается в том, что наряду с движением электронов вокруг ядер в молекуле происходит колебание самих ядер относительно положения равновесия и вращение молекул как целого. Этим трем видам движений соответствуют три типа квантовых уровней энергии: электронные, колебательные и вращательные. В первом приближении движения можно считать независимыми. При изучении молекулярных спектров чрезвычайно важно то обстоятельство, что масса ядра более чем на три порядка превосходит электронную:

Поэтому скорости движения ядер в молекуле малы по сравнению со скоростями электронов. Движение электронов мгновенно приспосабливается к изменению расположения ядер. Таким образом, конфигурацию ядер можно рассматривать как параметр при определении уровней энергии . Полная энергия молекулы E складывается, соответственно, из трех квантованных значений энергий

Электронные уровни энергии. Молекула, подобно атому, обладает рядом возбужденных состояний, различающихся строением электронной оболочки. Переходы электрона из одного состояния в другое связаны с поглощением или испусканием квантов света. Порядок энергии электронных уровней молекулы можно оценить из соотношения неопределенностей Гейзенберга, аналогично тому, как была получена энергия основного состояния атома водорода. Если линейные размеры молекулы водорода , то энергия уровня

что при типичных значениях

составляет несколько электрон-вольт и соответствует переходам с испусканием квантов в видимой и ультрафиолетовой областях спектра.

Энергия колебательного движения ядер. Движение ядер в молекуле можно рассматривать при заданном электронном состоянии. Изучение относительного движения ядер с массам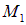и и в молекуле сводится к решению задачи о поведении частицы с приведенной массой

во внешнем для нее потенциальном поле. Для заданного связанного электронного состояния молекулы энергия E(R) имеет минимум, когда ядра расположены на расстоянии . Разложим E(R) в ряд Тейлора вблизи точки минимума по степеням
():

С точностью до постоянной энергия движения ядер пропорциональна квадрату расстояния от положения равновесия. Следовательно, эти атомы колеблются под действием квазиупругой силы

Квантовая механика (см. разд. 3.3) позволяет определить энергетические состояния такой колебательной системы (гармонического осциллятора), которые образуют совокупность эквидистантных (равноотстоящих) уровней (3.15):

где — колебательное (вибрационное) квантовое число, а частота

совпадает с частотой классического осциллятора. Переходы между колебательными уровнями подчиняются правилу отбора

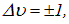
то есть вибрационное число при переходе может измениться лишь на единицу.

Для оценки порядка величины энергии колебательного движения заметим, что при амплитуде колебаний порядка расстояния между ядрами молекула диссоциирует (разваливается). Энергия таких колебаний составляет величину порядка

С другой стороны, изменение энергии при амплитуде колебаний близко к величине электронной энергии . Действительно, изменение межъядерного расстояния на величину должно вызывать существенные искажения электронной волновой функции 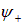, то есть возбуждение электронов с изменением их энергии на величину порядка . Таким образом, получаем оценку «коэффициента жесткости» молекулярного осциллятора:

(см. соотношение (8.11)), а также энергии колебательного движения

Это величина порядка десятых или сотых долей электрон-вольта и соответствует излучению в инфракрасной области спектра. Таким образом, колебательная энергия много меньше энергии электронного уровня.

Энергия вращательного движения молекул. Вращение молекул рассмотрим в предположении жесткой связи между ядрами, то есть пренебрегая колебаниями. Для двухатомной молекулы момент инерции относительно оси, перпендикулярной оси молекулы и проходящий через центр инерции, равен

Согласно законам механики, энергия вращательного движения связана с вращательным моментом импульса L молекулы выражением

Вращательный момент квантуется:

где J = 0, 1, 2, ... — ротационное квантовое число. Это позволяет определить вращательные уровни энергии:

Отсюда следует оценка величины вращательной энергии:

то есть величину порядка

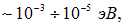
соответствующую излучению в далекой инфракрасной и микроволновой (СВЧ) областях спектра. Для вращательного спектра разрешены переходы с

Молекулярные спектры. Проведенные оценки величины трех типов уровней в молекуле показывают, что

В соответствии с этими отношениями система уровней молекулы складывается из сравнительно далеко отстоящих электронных уровней, испытывающих расщепление под влиянием колебаний ядер. Эти расщепленные уровни, в свою очередь, испытывают еще более тонкое расщепление в связи с вращением молекул (рис. 8.8).

Рис. 8.8. Схема расположения электронных, вращательных и колебательных уровней энергии молекулы

Изменение электронного состояния молекулы связано обычно с целой серией изменений: колебательное движение претерпевает изменения, так как новому состоянию соответствует измененное равновесное расстояние между ядрами; при этом также изменяется и момент инерции молекулы и, следовательно, положение вращательных уровней. Эти изменения вызывают целую серию поглощаемых или испускаемых квантов, энергии которых соответствуют разнице энергий каких-либо уровней, между которыми происходит переход.

Если атомные спектры состоят из отдельных линий, то при наблюдении с низким разрешением молекулярные спектры представляются состоящими из полос. При применении приборов с высокой разрешающей способностью обнаруживается, что полосы состоят из большого числа тесно расположенных линий. В соответствии с их характером спектры молекул носят название полосатых спектров. В зависимости от того, изменение каких видов энергии (электронной, колебательной или вращательной) вызывает испускание молекулой фотона, различают следующие типы полос: 1) вращательные; 2) колебательно-вращательные; 3) электронно-колебательные.

В основном состоянии молекулы все три вида энергии имеют минимальное значение. При сообщении молекуле достаточного количества энергии она переходит в возбужденное состояние и затем, совершая разрешенный правилами отбора переход в одно из более низких энергетических состояний, излучает фотон с энергией

Следует отметить, что значения частоты и момента инерции I зависят от электронных конфигураций молекулы и поэтому обозначены одним и двумя штрихами.

Учитывая соотношения между энергиями

приходим к выводу, что при слабых возбуждениях изменяется только при более сильных — , и лишь при еще более сильных возбуждениях изменяется электронная конфигурация молекулы, то есть . Соответственно, наименьшей энергией обладают фотоны, связанные с вращательными переходами (электронная конфигурация и энергия колебательного движения не изменяются). Учитывая, что 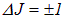, находим

Измерение энергии таких фотонов позволяет определить момент инерции молекулы и, следовательно, ее размер . Например, для НCl найдено 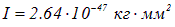, что соответствует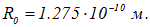

При переходах, сопровождающихся изменениями и колебательного, и вращательного состояний молекулы, частота излучаемого фотона может быть записана в виде

где было учтено, что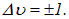

8.4. Комбинационное рассеяние света

В 1928 г. советские ученые Г.С. Ландсберг и Л.И. Мандельштам и одновременно индийские физики Ч. Раман и К. Кришнан обнаружили, что в спектре рассеяния, возникающем при прохождении света через газы, жидкости или прозрачные кристаллические тела, помимо несмещенной линии с частотой падающего света могут содержаться новые линии, частоты которых представляют комбинации частоты падающего света и частоты 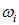, колебательных или вращательных переходов рассеивающих молекул:

Это явление получило название комбинационного (рамановского) рассеяния света, и за его открытие Раман был удостоен в 1930 г. Нобелевской премии.

Из рис. 8.9 видно, что спектр комбинационного рассеяния состоит из несмещенной линии 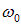, симметрично которой располагается ряд спутников. Каждому «красному» спутнику (то есть спутнику, смещенному в сторону больших длин волн) с частотой 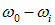(стоксовы линии), соответствует «фиолетовый» спутник с частотой (антистоксовы линии).

Рис. 8.9. Спектр комбинационного рассеяния

При обычных температурах интенсивность фиолетовых спутников значительно меньше, чем красных. С увеличением температуры интенсивность фиолетовых спутников быстро возрастает.

Процесс рассеяния света в рамках квантовой теории можно рассматривать как соударение фотонов с молекулами (упругое и неупругое). При соударении фотон может отдать молекуле или получить от нее только такие количества энергии, которые равны разностям двух ее энергетических уровней. Рассеяние фотона с энергией может сопровождаться переходами молекулы между различными вращательными или колебательными уровнями и т. д. Если при столкновении с фотоном молекула переходит из состояния с энергией в состояние с энергией 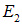(причем ), то энергия фотона после рассеяния уменьшается:

где

то есть возникает красный спутник в спектре.

Если же первоначально молекула находилась в возбужденном состоянии с энергией , она может в результате взаимодействия с фотоном перейти в состояние с энергией , отдав избыток энергии фотону. В результате этого энергия фотона увеличивается:

то есть возникает фиолетовый спутник. Таким образом, может возникнуть ряд симметрично расположенных спутников.

При обычных температурах число молекул, находящихся в основном состоянии, намного превосходит число молекул, находящихся в возбужденных состояниях. Поэтому столкновения, сопровождающиеся увеличением энергии молекулы, происходят чаще, чем переходы, сопровождающиеся уменьшением энергии. Этим объясняется большая интенсивность красных спутников по сравнению с фиолетовыми. При увеличении температуры число молекул в возбужденных энергетических состояниях быстро растет, что обусловливает увеличение интенсивности фиолетовых спутников.

Следует отметить, что комбинационное рассеяние относится к числу нелинейных эффектов квантовой теории излучения. Оно стало эффективным методом исследования строения молекул и их взаимодействия со средой. Методами комбинационного рассеяния изучают квазичастицы в твердом теле. Применение лазеров в качестве источников света значительно расширило круг объектов (газы, порошки), доступных для исследования методами комбинационного рассеяния света.

Исследование, описанное в статье про физика химической связи, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое физика химической связи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Атомная и Ядерная физика