Лекция
Привет, Вы узнаете о том , что такое квантовая природа излучения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое квантовая природа излучения , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.
Два века борьбы корпускулярной и волновой теорий света завершились победой последней. Уравнения Максвелла стали венцом теоретической физики XIX в. На горизонте науки виднелись лишь два темных пятнышка — проблемы с тепловым излучением и результат опыта Майкельсона. Казалось, что еще немного, и физики останутся без работы: законы природы представлялись в основном понятыми. К счастью, так не случилось. Из одного пятнышка выросла квантовая теория, из другого — теория относительности. С теорией относительности мы познакомились в первой части курса. Настало время приоткрыть двери в квантовый мир.
|
Тепловое излучение — это электромагнитное излучение, испускаемое веществом за счет запасов его внутренней (тепловой) энергии. |
Поэтому характеристики теплового излучения (интенсивность, спектральный состав) зависят от температуры излучающего вещества. Все прочие виды электромагнитного излучения существуют за счет других, не тепловых, форм энергии. Тепловое излучение — единственный вид излучения, которое может находиться в термодинамическом равновесии с веществом и само быть при этом в состоянии термодинамического равновесия. Ниже будет рассматриваться главным образом термодинамически равновесное тепловое излучение.
Предположим, что нагретое тело помещено в полость, стенки которой поддерживаются при некоторой постоянной температуре 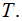 Если в полости нет никакой среды (газа), то обмен энергией между оболочкой и телом происходит только за счет процессов поглощения, испускания и отражения теплового излучения веществом стенки полости. С течением времени температура тела станет равной температуре оболочки и наступит динамическое равновесие — в единицу времени тело будет поглощать столько же энергии, сколько и излучать. Очевидно, что при этом и излучение, заполняющее полость, будет находиться в равновесии, как с телом, так и со стенками полости. Допустим, что равновесие между телом и излучением нарушено и тело излучает энергии больше, чем поглощает. Тогда температура тела и его внутренняя энергия начнут убывать, что приведет к уменьшению излучаемой телом энергии. Температура тела будет понижаться до тех пор, пока количество излучаемой телом энергии не станет равным количеству поглощаемой энергии. Если равновесие нарушится в другую сторону, то есть тело будет излучать меньше энергии, чем поглощает, то температура тела будет возрастать до тех пор, пока снова не установится равновесие. Таким образом, нарушение равновесия между телом и тепловым излучением вызывает процессы, направленные в сторону восстановления равновесия.
Если в полости нет никакой среды (газа), то обмен энергией между оболочкой и телом происходит только за счет процессов поглощения, испускания и отражения теплового излучения веществом стенки полости. С течением времени температура тела станет равной температуре оболочки и наступит динамическое равновесие — в единицу времени тело будет поглощать столько же энергии, сколько и излучать. Очевидно, что при этом и излучение, заполняющее полость, будет находиться в равновесии, как с телом, так и со стенками полости. Допустим, что равновесие между телом и излучением нарушено и тело излучает энергии больше, чем поглощает. Тогда температура тела и его внутренняя энергия начнут убывать, что приведет к уменьшению излучаемой телом энергии. Температура тела будет понижаться до тех пор, пока количество излучаемой телом энергии не станет равным количеству поглощаемой энергии. Если равновесие нарушится в другую сторону, то есть тело будет излучать меньше энергии, чем поглощает, то температура тела будет возрастать до тех пор, пока снова не установится равновесие. Таким образом, нарушение равновесия между телом и тепловым излучением вызывает процессы, направленные в сторону восстановления равновесия.
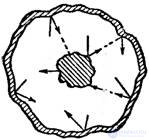
Рис. 1.1. Нагретое тело в полости с идеально отражающими стенками
Представим теперь то же самое тело, помещенное внутри другой оболочки, отличающейся размерами, формой или материалом, из которого она сделана. Будем поддерживать ту же самую температуру оболочки. В системе пойдут аналогичные процессы установления равновесия, в результате которых тело внутри оболочки нагреется до той же самой температуры Т. Для тела внутри оболочки ничего не изменилось: оно находится при той же самой температуре, что и прежде, и, следовательно, будет излучать ту же самую энергию. Так как тело находится в равновесии с излучением внутри оболочки, мы приходим к выводу, что характеристики этого излучения не зависят от свойств оболочки, но лишь от ее температуры. Это «стандартное», термодинамически равновесное излучение называется излучением абсолютно черного тела. О том, откуда такое название и что такое абсолютно черное тело будет сказано ниже. Равновесное излучение можно охарактеризовать плотностью энергии 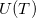 , зависящей только от температуры.
, зависящей только от температуры.
|
Плотность энергии |
Тепловое излучение состоит из электромагнитных волн разных частот. Полная плотность энергии складывается из плотностей энергий этих волн. Для более детальной характеристики излучения вводят дифференциальную величину — спектральную плотность энергии излучения 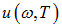 .
.
|
Спектральная плотность энергии излучения — это энергия излучения в единице объема, приходящаяся на единичный интервал частот. |
Иными словами, если обозначить через 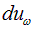 энергию излучения в единице объема, приходящуюся на волны с частотами от
энергию излучения в единице объема, приходящуюся на волны с частотами от 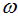 до
до 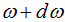 , то
, то
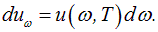
|
В системе СИ спектральная плотность энергии измеряется в следующих единицах:
|
Плотность энергии 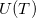 есть сумма спектральных плотностей энергии по всем возможным частотам, то есть выражается интегралом
есть сумма спектральных плотностей энергии по всем возможным частотам, то есть выражается интегралом
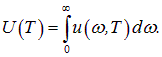
Итак, в полости, существует стандартное излучение с плотностью энергии 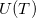 . Рассмотрим теперь тело, находящееся с ним в равновесии.
. Рассмотрим теперь тело, находящееся с ним в равновесии.
|
Энергетическая светимость R (интегральная плотность потока энергии излучения) — равна энергии, испускаемой в единицу времени единицей поверхности излучающего тела по всем направлениям. |
|
В системе СИ энергетическая светимость измеряется в
|
Энергетическая светимость зависит от температуры тела. Тепловое излучение состоит из волн различных частот. Для характеристики теплового излучения важно знать, какая энергия, в каком диапазоне частот излучается телом. Поэтому вводят дифференциальную характеристику 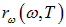 , называемую испускательной способностью тела, являющуюся спектральной плотностью потока энергии излучения.
, называемую испускательной способностью тела, являющуюся спектральной плотностью потока энергии излучения.
|
Испускательная способность тела (спектральная плотность потока энергии излучения) — это количество энергии, испускаемой в единицу времени единицей поверхности тела в единичном интервале частот по всем направлениям. |
Чтобы получить энергетическую светимость тела, надо проинтегрировать испускательную способность по всем частотам:
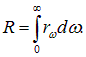
|
В системе СИ испускательная способность тела (спектральная плотность потока энергии излучения) измеряется в Дж/м2:
|
Нагретое тело не только испускает энергию, но и поглощает ее. Для описания способности тела поглощать энергию падающего на его поверхность излучения вводится величина, которая так и называется: поглощательная способность.
|
Поглощательная способность |
Поглощательная способность равна той доли, которую — в заданном спектральном интервале 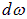 — поглощенная энергия излучения
— поглощенная энергия излучения 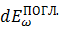 составляет от падающей
составляет от падающей 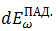 энергии излучения. Другими словами:
энергии излучения. Другими словами:
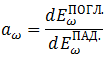
Очевидно, что поглощательная способность тела является безразмерной величиной, не превышающей единицу.
|
Абсолютно черное тело — это тело, способное поглощать при любой температуре все падающее на него излучение всех частот. |
Для абсолютно черного тела
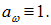
Тел с такими свойствами в природе не бывает, это очередная физическая идеализация.
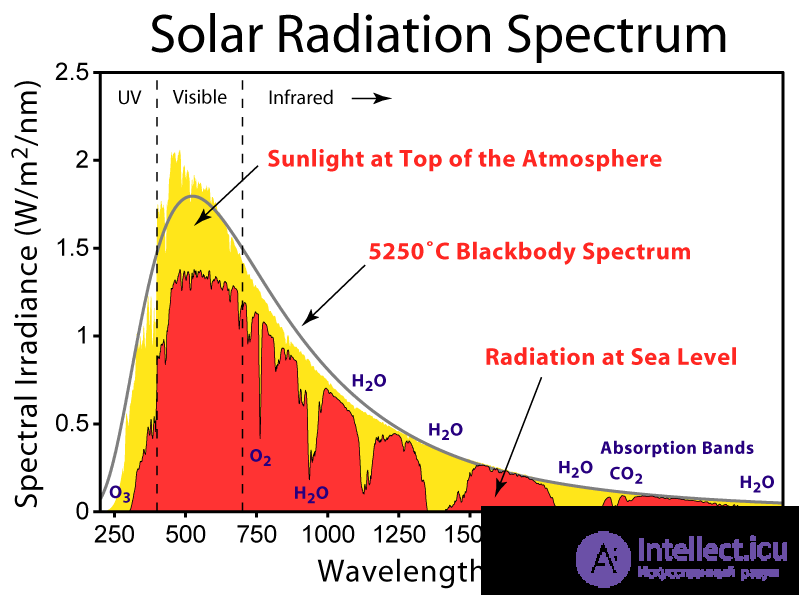
Рис. 1.2. Спектр излучения абсолютно черного тела (черная линия) при температуре 5250 °С хорошо моделирует излучение Солнца. Красным цветом показаны результаты измерений на уровне моря, желтым — в верхней атмосфере.
Будем поочередно помещать в полость различные тела. Все они находятся в одинаковых условиях, в окружении одного и того же излучения. Обозначим 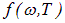 энергию, падающую в единицу времени на единицу поверхности тела в единичном интервале частот. Согласно определению поглощательной способности тело поглощает энергию
энергию, падающую в единицу времени на единицу поверхности тела в единичном интервале частот. Согласно определению поглощательной способности тело поглощает энергию 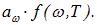 В состоянии равновесия эта энергия должна быть равна испущенной телом энергии:
В состоянии равновесия эта энергия должна быть равна испущенной телом энергии:
|
|
|
(1.1) |
Различные тела в полости имеют разную поглощательную способность, следовательно, у них будет и разная испускательная способность, так что отношение rw /аw не зависит от конкретного тела, помещенного в полость:
|
|
|
(1.2) |
С другой стороны, испускательная способность тела не зависит от полости, в которую оно помещено, но лишь от свойств тела. Таким образом, функция 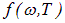 есть универсальная функция частоты и температуры, не зависящая ни от свойств полости, ни от характеристик тела в ней. Соотношение (1.2) выражает закон Кирхгофа.
есть универсальная функция частоты и температуры, не зависящая ни от свойств полости, ни от характеристик тела в ней. Соотношение (1.2) выражает закон Кирхгофа.
|
Отношение испускательной и поглощательной способности тела не зависит от природы тела. Для всех тел функция |
Строго говоря, сформулированное выше утверждение справедливо в условиях термодинамического равновесия, наличие которого здесь и ниже всегда предполагается.
Для абсолютно черного тела
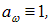
откуда следует физическая интерпретация универсальной функции Кирхгофа 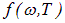 : она представляет собой испускательную способность абсолютно черного тела, то есть
: она представляет собой испускательную способность абсолютно черного тела, то есть
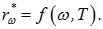
(Характеристики абсолютно черного тела будем помечать звездочкой, а само тело называть нередко просто «черным», а не абсолютно черным).

Рис. 1.3. Густав Роберт Кирхгоф (1824–1887)
Установим теперь связь между испускательной способностью черного тела 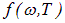 и спектральной плотностью
и спектральной плотностью 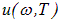 стандартного излучения в полости (выше мы назвали его излучением черного тела). Сравнивая размерности этих величин, видим, что отношение
стандартного излучения в полости (выше мы назвали его излучением черного тела). Сравнивая размерности этих величин, видим, что отношение 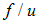 имеет размерность скорости. Единственная величина, имеющая размерность скорости, которая ассоциируется с электромагнитными волнами в вакууме, — это скорость света
имеет размерность скорости. Единственная величина, имеющая размерность скорости, которая ассоциируется с электромагнитными волнами в вакууме, — это скорость света 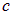 . Поэтому искомое соотношение должно иметь вид
. Поэтому искомое соотношение должно иметь вид
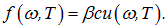
Найдем безразмерный коэффициент пропорциональности 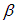 в этой формуле. В качестве модели абсолютно черного тела возьмем замкнутую полость с небольшим отверстием s (рис. 1.4).
в этой формуле. В качестве модели абсолютно черного тела возьмем замкнутую полость с небольшим отверстием s (рис. 1.4).
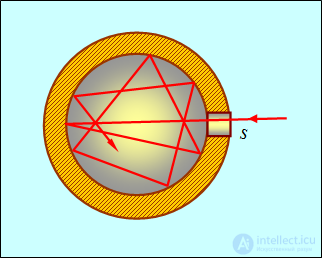
Рис. 1.4. Полocть с небольшим отверстием — реализация черного тела
Луч света, падающий внутрь этой полости через отверстие s, претерпевает многократное отражение. При каждом отражении стенки полости поглощают часть энергии. Поэтому интенсивность луча света, выходящего из отверстия, во много раз меньше интенсивности входящего луча. Чем больше отношение площади полости к площади отверстия, тем ближе такое тело к абсолютно черному. Поэтому отверстие в полости излучает как абстрактное черное тело.
С другой стороны, внутри полости существует равновесное тепловое излучение со спектральной плотностью U. Подсчитаем энергию dW0 , выходящую из отверстия площадью s в телесном угле 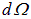 в направлении, заданном углом
в направлении, заданном углом 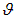 . Во-первых, в данном направлении за время
. Во-первых, в данном направлении за время 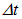 может выйти только энергия, содержащаяся в наклонном цилиндре с площадью основания s и длиной образующей с
может выйти только энергия, содержащаяся в наклонном цилиндре с площадью основания s и длиной образующей с 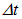 (рис. 1.5-1).
(рис. 1.5-1).
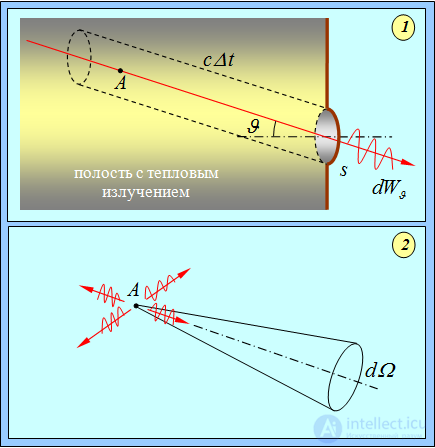
Рис. 1.5. Тепловое излучение из отверстия в полости
Объем такого цилиндра равен
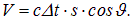
Содержащаяся в нем энергия теплового излучения равна
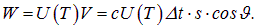
Но не вся она распространяется под углом 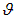 . Тепловое излучение распространяется по всем направлениям с равной вероятностью (рис. 1.5-2). Поэтому в телесный угол
. Тепловое излучение распространяется по всем направлениям с равной вероятностью (рис. 1.5-2). Поэтому в телесный угол 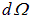 попадет только часть энергии (мы обозначим эту долю как
попадет только часть энергии (мы обозначим эту долю как 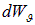 ), пропорциональная величине телесного угла
), пропорциональная величине телесного угла
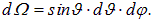
Так как полный телесный угол равен 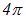 , имеем
, имеем
|
|
|
(1.3) |
Теперь осталось проинтегрировать 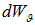 по углам
по углам 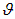 и
и 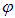 , чтобы получить полную энергию
, чтобы получить полную энергию 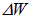 , выходящую из отверстия полости. Об этом говорит сайт https://intellect.icu . Обращаем внимание: излучение падает на отверстие только из левого полупространства, так что полярный угол
, выходящую из отверстия полости. Об этом говорит сайт https://intellect.icu . Обращаем внимание: излучение падает на отверстие только из левого полупространства, так что полярный угол 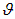 меняется в пределах от нуля до
меняется в пределах от нуля до 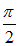 (угол
(угол 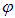 меняется как обычно от 0 до
меняется как обычно от 0 до 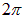 ). Интегрирование по
). Интегрирование по 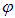 дает множитель
дает множитель 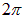 , интегрируя по
, интегрируя по 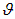 , окончательно получаем:
, окончательно получаем:
|
|
|
(1.4) |
Разделив 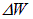 на время
на время 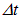 и площадь отверстия s, получим энергетическую светимость черного тела R*, а также искомый коэффициент пропорциональности
и площадь отверстия s, получим энергетическую светимость черного тела R*, а также искомый коэффициент пропорциональности
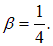
Итак, энергетическая светимость черного тела 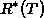 связана с плотностью энергии в полости
связана с плотностью энергии в полости 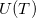 соотношением
соотношением
|
|
|
(1.5) |
Аналогичное соотношение справедливо для спектральных характеристик излучения черного тела:
|
|
|
(1.6) |
Таким образом, универсальная функция 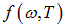 в законе Кирхгофа, представляющая собой испускательную способность черного тела, с точностью до множителя с/4 совпадает также со спектральной плотностью равновесного теплового излучения.
в законе Кирхгофа, представляющая собой испускательную способность черного тела, с точностью до множителя с/4 совпадает также со спектральной плотностью равновесного теплового излучения.
До сих пор мы относили спектральные характеристики теплового излучения к единичному интервалу частоты. Можно определить аналогичные характеристики, отнесенные к единичному интервалу длин волн. Так, черное тело испускает в интервале частот 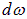 энергию
энергию 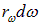 . Эту же энергию можно записать как
. Эту же энергию можно записать как 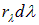 . Интервалу частот
. Интервалу частот 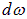 соответствует интервал длин волн
соответствует интервал длин волн 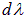 . Учитывая соотношения
. Учитывая соотношения
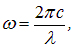
находим
|
|
|
(1.7) |
где знак минус указывает на то, что с возрастанием частоты 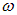 длина волны
длина волны 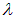 убывает. Поэтому в дальнейшем, в соотношениях связывающих длины интервалов, знак минус будем опускать. Таким образом,
убывает. Поэтому в дальнейшем, в соотношениях связывающих длины интервалов, знак минус будем опускать. Таким образом,
|
|
|
(1.8) |
или
|
|
|
(1.9) |
Аналогичным образом можно записать выражения для спектральной плотности энергии.
Изучение распределения энергии в спектре теплового излучения абсолютно черного тела при различных температурах привело к экспериментальному установлению следующих закономерностей.
|
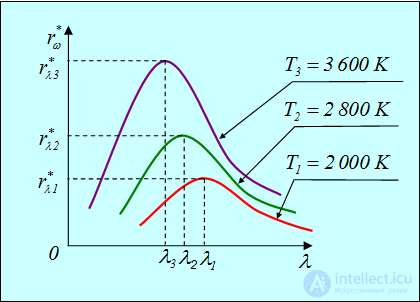
Рис. 1.6. Испускательная способность черного тела при разных температурах
Если нагревать любое тело, то оно вначале краснеет, а с повышением температуры свечение тела становится все более белым. Это свидетельствует о том, что максимум интенсивности теплового излучения по мере повышения температуры тела смещается к фиолетовому концу спектра, то есть к его коротковолновой части. Длина волны 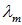 в спектре излучения абсолютно черного тела, на которую приходится максимум спектральной плотности энергетической светимости, определяется законом смещения Вина:
в спектре излучения абсолютно черного тела, на которую приходится максимум спектральной плотности энергетической светимости, определяется законом смещения Вина:
|
|
|
(1.10) |
где постоянная Вина 
Видео 1.3. Закон смещения Вина.
Австрийский физик Й. Стефан, анализировавший экспериментальные данные, и Л. Больцман, исходивший из общих термодинамических соображений, установили зависимость энергетической светимости абсолютно черного тела от температуры. Согласно закону Стефана — Больцмана,
|
Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры
|
Экспериментально найденный коэффициент пропорциональности — постоянная Стефана — Больцмана — оказался равным 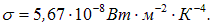

Рис. 1.7. Вин Вильгельм (1864–1928)

Рис. 1.8. Стефан Йозеф (1835–1893)

Рис. 1.9. Больцман Людвиг (1844–1906)
Несмотря на детальное изучение характеристик теплового излучения, математический вид функций 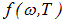 и
и 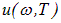 долгое время оставался для физиков загадкой.
долгое время оставался для физиков загадкой.
Попытка строгого теоретического вывода зависимости 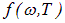 принадлежит английским ученым Дж. Рэлею и Дж. Джинсу. Воспроизведем их аргументы. Пусть полость представляет собой прямоугольный ящик с линейными размерами Lx, Ly, Lz вдоль соответствующих координатных осей. Рассмотрим стоячие электромагнитные волны вдоль оси х. Эти волны эквивалентны стоячим волнам, возникающим в струне. Их длины волн
принадлежит английским ученым Дж. Рэлею и Дж. Джинсу. Воспроизведем их аргументы. Пусть полость представляет собой прямоугольный ящик с линейными размерами Lx, Ly, Lz вдоль соответствующих координатных осей. Рассмотрим стоячие электромагнитные волны вдоль оси х. Эти волны эквивалентны стоячим волнам, возникающим в струне. Их длины волн 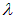 должны удовлетворять соотношению
должны удовлетворять соотношению
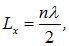
откуда для проекции волнового вектора находим
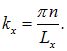
Число 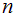 нумерует разные типы волн, существующих на струне длины Lx. Поэтому число типов стоячих электромагнитных волн с проекциями волнового вектора в интервале от kx до kx + dkx равно
нумерует разные типы волн, существующих на струне длины Lx. Поэтому число типов стоячих электромагнитных волн с проекциями волнового вектора в интервале от kx до kx + dkx равно
|
|
|
(1.12) |
Мы уменьшили результат в два раза, потому что стоячие волны с волновыми числами kx и –kx — это одно и то же колебание (направления распространения для стоячих волн не существует).

Рис. 1.10. Джинс Джеймс Хопвуд (1877–1946)

Рис. 1.11. Рэлей Джон Уильям (1842–1919)
Аналогичные формулы можно записать для стоячих электромагнитных волн вдоль осей y и z:
|
|
|
(1.13) |
Перемножая эти соотношения, находим полное число типов колебаний в прямоугольной полости, волновые векторы которых лежат в интервале от 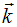 до
до 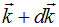
|
|
|
(1.14) |
Здесь мы увеличили результат в два раза, чтобы учесть поперечность электромагнитных волн: при данной длине волны колебания могут осуществляться в двух взаимно ортогональных направлениях.
Учитывая, что частота определяется только модулем волнового вектора и не зависит от его направления, перейдем к сферическим координатам, проинтегрируем по углам (учтем все направления), то есть произведем замену
|
|
|
(1.15) |
Тогда выражение (1.14) для 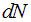 приобретет вид:
приобретет вид:
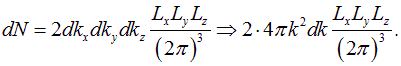
Учитывая, что
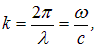
получаем (опуская знак «минус»)
|
|
|
(1.16) |
Произведение
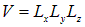
есть объем полости. Находим тогда для числа типов колебаний, приходящихся на единичный объем:
|
|
|
(1.17) |
Далее Рэлей и Джине применили классическую теорему о равнораспределении энергии по степеням свободы, согласно которой на каждую степень свободы в классической статистической системе приходится энергия
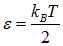
(здесь kB — постоянная Больцмана). У гармонического осциллятора средняя кинетическая энергия равна средней потенциальной, и поэтому его средняя энергия равна kBТ. Аналогично в электромагнитной волне колеблются векторы напряженностей электрического и магнитного поля, которые дают одинаковый вклад в средний поток энергии. Поэтому для спектральной плотности энергии излучения Рэлей и Джине нашли выражения:
|
|
|
(1.18) |
Соответственно, для испускательной способности абсолютно черного тела были получены соотношения:
|
|
|
(1.19) |
Для длинных волн формула Рэлея — Джинса дает хорошее совпадение с экспериментальными данными, но для коротких волн, то есть в области больших частот, расчетные значения спектральной плотности 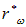 перестают совпадать с экспериментом (кривая уходит на бесконечность). Кроме того, энергетическая светимость черного тела также получается бесконечной:
перестают совпадать с экспериментом (кривая уходит на бесконечность). Кроме того, энергетическая светимость черного тела также получается бесконечной:
|
|
|
(1.20) |
Создавшееся положение было названо «ультрафиолетовой катастрофой». Таким образом, классическая физика оказалась не в состоянии объяснить важные экспериментальные данные.
М. Планк указал выход из создавшегося положения, выдвинув гипотезу, что электромагнитная энергия испускается и поглощается не непрерывно, а отдельными порциями (квантами)
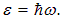
Коэффициент пропорциональности в соотношении между энергией 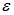 и частотой света
и частотой света 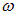 в СИ измеряется в Дж∙с и называется теперь постоянной Планка. Впоследствии было установлено ее численное значение:
в СИ измеряется в Дж∙с и называется теперь постоянной Планка. Впоследствии было установлено ее численное значение:
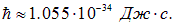
В соответствии с гипотезой Планка, энергия 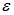 рассмотренной выше стоячей волны в резонаторе может принимать лишь дискретный набор значений
рассмотренной выше стоячей волны в резонаторе может принимать лишь дискретный набор значений
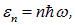
кратных частоте волны.
Рис. 1.12. Планк Макс Карл Эрнст Людвиг (1858–1947)
Используя это соотношение, Планк получил аналитическое выражение для испускательной способности черного тела. Для излучения в состоянии термодинамического равновесия по-прежнему справедливо распределение Больцмана. Соответственно, вероятность Рn того, что энергия стоячей волны с частотой 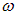 равна
равна
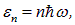
определяется формулой
|
|
|
(1.21) |
Сумма всех вероятностей равна единице, откуда мы находим нормировочный коэффициент С:
|
|
|
(1.22) |
Средняя энергия колебания с частотой w равна
|
|
|
(1.23) |
Метод расчета таких сумм основан на выражении для суммы членов геометрической прогрессии и формулы, получаемой из нее дифференцированием:
|
|
|
(1.24) |
Подставляя сюда
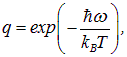
находим выражение для средней энергии стоячей волны
|
|
|
(1.25) |
Умножая число стоячих волн в единице объема и с частотой в интервале 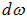 на их среднюю энергию (1.25), получаем формулу Планка для спектральной плотности энергии теплового излучения
на их среднюю энергию (1.25), получаем формулу Планка для спектральной плотности энергии теплового излучения
|
|
|
(1.26) |
Испускательная способность абсолютно черного тела с учетом формулы (1.6) описывается законом Планка
|
|
|
(1.27) |
При высоких температурах (малых частотах)
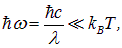
экспоненту в знаменателе формул (1.25) и (1.27) можно разложить в ряд:
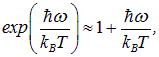
откуда получаем классическое выражение для средней энергии осциллятора
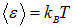
и формулу Рэлея — Джинса (1.19). Для спектральной плотности энергии и испускательной способности абсолютно черного тела в зависимости от длины волны 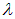 имеем
имеем
|
|
|
(1.28) |
Оказалось, что закон Планка точно согласуется с экспериментальными данными во всем интервале длин волн, в то время как формула Рэлея — Джинса, как уже говорилось, соответствует данным опыта только при больших длинах волн (рис. 1.13).
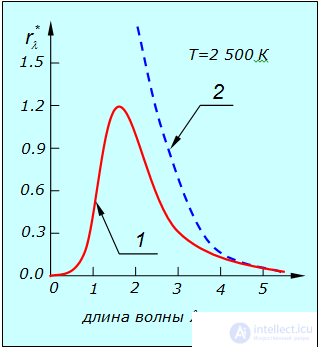
Рис. 1.13. Сравнение испускательной способности черного тела 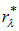 ,
,
согласно закону Планка и эксперименту (1) и формуле Рэлея — Джинса (2)
Более того, из закона Планка непосредственно получается закон Стефана — Больцмана:
|
|
|
(1.29) |
Введем безразмерную переменную интегрирования
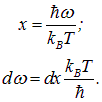
В результате этого получаем
|
|
|
(1.30) |
Используя значение интеграла
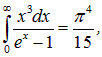
находим аналитическое выражение для постоянной Стефана — Больцмана:
|
|
|
(1.31) |
величина которой согласуется с приведенными экспериментальными данными.
Из закона Планка следует также закон смещения Вина. Если продифференцировать функцию Планка (1.28) по 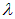 , и приравнять нулю производную, то можно найти положение максимума функции
, и приравнять нулю производную, то можно найти положение максимума функции 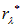 . Действительно, приравнивая нулю функцию
. Действительно, приравнивая нулю функцию 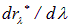 , получаем
, получаем
|
|
|
(1.32) |
Введя безразмерную переменную
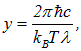
приходим к уравнению
|
|
|
(1.33) |
Корень этого уравнения
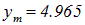
позволяет получить закон смещения Вина:
|
|
|
(1.34) |
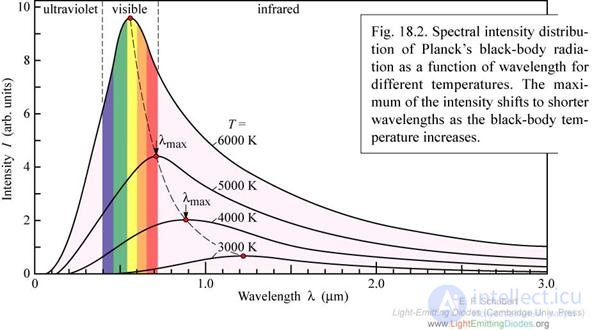
Рис. 1.14. Распределение Планка для испускательной способности абсолютно черного тела при разных температурах. С ростом температуры максимум спектров сдвигается вдоль пунктирной линии в строну коротких длин волн в соответствии с законом Вина
Таким образом, формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе все эмпирические законы теплового излучения, а также позволяет вычислить константы в этих законах.
Мы искали максимум функции 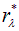 по длинам волн. Но излучение черного тела можно характеризовать также и распределением (1.27)
по длинам волн. Но излучение черного тела можно характеризовать также и распределением (1.27) 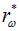 по частотам. Найдем для сравнения максимум этого распределения. Для этого надо найти экстремум функции (1.27):
по частотам. Найдем для сравнения максимум этого распределения. Для этого надо найти экстремум функции (1.27):
|
|
|
(1.35) |
Вводя безразмерную переменную
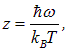
получаем уравнение для точки максимума распределения 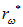 :
:
|
|
|
(1.36) |
которое имеет корень
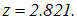
Отсюда следует, что максимум интенсивности 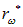 приходится на частоту
приходится на частоту
|
|
|
(1.37) |
Этой частоте соответствует длина волны
|
|
|
(1.38) |
которая, конечно, не определяет максимум функции (1.28) и поэтому не совпадает с выражением (1.34) для 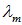 из закона смещения Вина:
из закона смещения Вина:
|
|
|
(1.39) |
Пример 1. Принимая, что Солнце излучает как абсолютно черное тело, вычислим его энергетическую светимость и температуру поверхности. Солнечный диск виден с Земли под углом 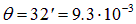 рад. Поток солнечной энергии на земной орбите (так называемая солнечная постоянная) равен С = 1.4 кВт/м2.
рад. Поток солнечной энергии на земной орбите (так называемая солнечная постоянная) равен С = 1.4 кВт/м2.
Пусть радиус Солнца равен rC , а расстояние до Земли есть lЗ . Их отношение связано с угловым диаметром Солнца:
|
|
|
(1.40) |
Если энергетическая светимость Солнца есть R, то полная энергия, излучаемая Солнцем в единицу времени, равна произведению R на площадь поверхности Солнца:
|
|
|
(1.41) |
Эта энергия достигает орбиты Земли, где она распределяется по большей площади 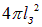 . Отсюда находим солнечную постоянную
. Отсюда находим солнечную постоянную
|
|
|
(1.42) |
В итоге получаем
|
|
|
(1.43) |
По формуле Стефана — Больцмана находим температуру верхних слоев Солнца
|
|
|
(1.44) |
Пример 2. В пророчестве Исайи (Ис. 30, 26) сказано:
«И свет луны будет, как свет солнца, а свет солнца будет светлее всемеро, как свет семи дней, в тот день, когда Господь обвяжет рану народа Своего и исцелит нанесенные ему язвы».
Оценим температуру окружающей среды в этот день.
Поток солнечного излучения, падающий на Землю, компенсируется энергией, излучаемой Землей. Из условия задачи следует, что в указанный день поток энергии (с учетом света Луны) в восемь раз превысит нынешний поток солнечного излучения. В состоянии теплового равновесия во столько же раз должен увеличиться поток тепловой энергии с Земли. Из закона Стефана — Больцмана следует, что температура на Земле должна возрасти в
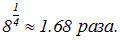
Если нынешняя средняя температура составляет 17° С = 290 К, то при увеличении потока энергии в 8 раз она составит Т = 1,68 ·290 = 487 К = 214 °С. Жарко будет!
Пример 3. Исходя из данных примера 1, найдем длину волны, на которую приходится максимум энергии солнечного излучения.
Выше была найдена температура верхних слоев Солнца. По закону смещения Вина получаем
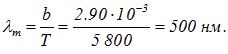
Исследование, описанное в статье про квантовая природа излучения, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое квантовая природа излучения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Атомная и Ядерная физика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика