3. Волновые свойства микрочастиц

Привет, Вы узнаете о том , что такое волновые свойства микрочастиц, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое волновые свойства микрочастиц , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.

Идеи квантовой физики всякий раз радикально ломали устоявшиеся представления об устройстве мира. Мы уже видели, как на новом уровне в волновую теорию проникли казалось давно отброшенные наукой корпускулы — фотоны, кванты света. В этой главе мы познакомимся с тем, как волны вторглись и заняли почетнейшее место в той области физики, которая давным-давно была хорошо обжита частицами. В определенном смысле квантовая физика совершила даже более революционный переворот в наших знаниях, чем теория относительности.

3.1. Атом Бора

Вернемся в 1911 год. К этому времени дискретность микромира проявилась наиболее ярко в атомных спектрах. Оказалось, что атомы поглощают и испускают свет только определенной длины волны, причем спектральные линии группируются в так называемые серии (рис. 3.1).

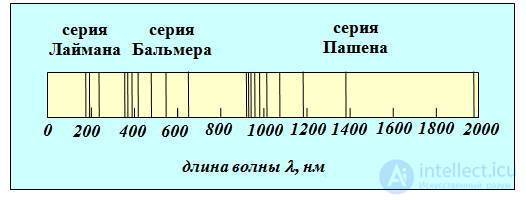
Рис. 3.1. Длины волн, излучаемые атомом водорода: спектр состоит из серий (показаны три первые) —
последовательностей линий, сгущающихся к некоторому (своему для каждой серии) предельному минимальному
значению 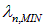; только четыре линии серии Бальмера лежат в видимом диапазоне

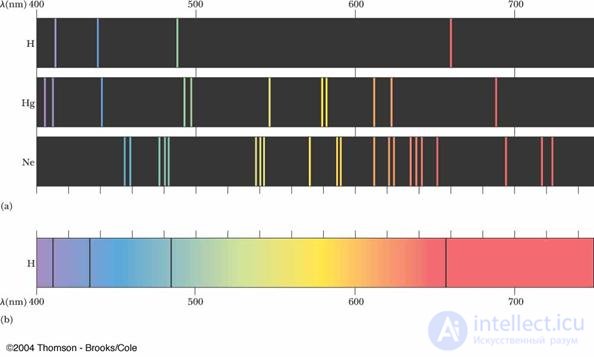
Рис. 3.2. (a) Линейчатые спектры излучения газообразных водорода, ртути и гелия: (b) спектр поглощения водорода

Рис. 3.3. Непрерывные спектры излучения дают нагретые твердые и жидкие вещества, сильно сжатые газы, высокотемпературная плазма

Для спектра водорода, простейшего из атомов, была установлена (не выведена, а угадана!) несложная формула

Здесь 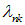— длина волны излучения атома водорода, n и k > n — целые числа, R — так называемая постоянная Ридберга (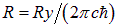, где 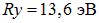— внесистемная единица энергии «Ридберг», равная половине атомной единице энергии). Оказалось, что серия Лаймана описывается этой формулой при значениях 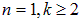, серия Бальмера — при 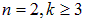, серия Пашена — при 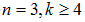и т. д. Предельные (минимальные) значения для длин волн получаются из (3.1) при :

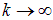Рис. 3.4. Йоханнес Роберт Ридберг (1854–1919)

Рис. 3.5. Теодор Лайман (1874–1954)

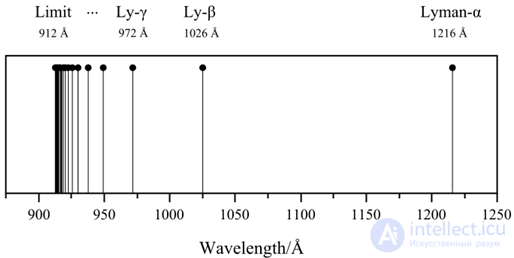
Рис. 3.6. Спектральная серия Лаймана

Рис. 3.7. Иоганн Якоб Бальмер (1825–1898)

Рис. 3.8. Видимые линии излучения водорода в серии Бальмера. Hα — красная линия справа, имеющая длину волны 656,3 нм. Самая левая линия — Hε, соответствует излучению уже в ультрафиолетовой области спектра на длине волны 397,0 нм

Рис. 3.9. Луис Карл Генрих Фридрих Пашен (1865–1947)

Рис. 3.10. Все линии серии Пашена расположены в инфракрасном диапазоне

Кроме того, в результате изучения свойств газов к тому времени было известно, что размеры атомов приблизительно
равны 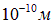. Поэтому теория, объясняющая спектр и размеры атомов, должна была включать в себя какой-то параметр, позволяющий построить величину с размерностью длины (постоянных e и m — заряда и массы электрона — для этого недостаточно). Такого параметра в классической теории не было. Им могла бы стать постоянная Ридберга, но ее происхождение было темно и загадочно.

В 1911 году Э. Резерфорд опубликовал теоретическую работу (Rutherford E., Philosophical Magazine, v. 21, p. 669–688, 1911), в которой на базе анализа экспериментов, выполненных в 1908–1909 годах его учениками — стажером Гансом Гейгером и аспирантом Эрнстом Марсденом — (Geiger H., Marsden T., Proceedings of the Royal Society of London, Series A, v. 82, p. 495–499, 1909) утверждал наличие внутри атома положительно заряженного ядра, в котором сосредоточена практически вся масса атома.

Рис. 3.11. Эрне́ст Ре́зерфорд (1871–1937)

В последствии, в одной из своих лекций сам Э. Резерфорд вспоминал о тех временах следующим образом (цитируется по книге Дж. Тригг, Решающие эксперименты в современной физике, Москва, «МИР», 1974, стр. 77): «…Я помню… ко мне пришел очень взволнованный Гейгер и сказал: «Мы, кажется, получили несколько случаев рассеяния 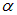— частиц назад…». Это самое невероятное событие, которое было в моей жизни. Это почти также невероятно, как если бы вы выстрелили 15-дюймовым снарядом в папиросную бумагу и он, отразившись от нее, попал бы в вас. При анализе этого я понял, что такое рассеяние назад должно быть результатом однократного столкновения и, проведя расчеты, увидел, что это никоим образом невозможно, если не предположить, что подавляющая часть массы атома сконцентрирована в крошечном ядре. Именно тогда у меня и зародилась идея об атоме с крошечным массивным центром, в котором сосредоточен заряд». От себя добавим, что слова «рассеяние назад» фактически означали рассеяние на 150 градусов, рассеяние на большие углы не позволяла наблюдать конструкция использованной в тот момент установки.

Принципиальная схема опытов Резерфорда представлена на рис. 3.12. Схему реальной установки можно найти в цитированной выше книге Дж. Тригга.

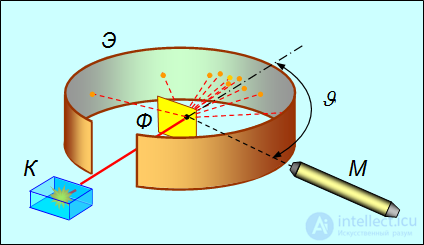
Рис. 3.12. Схема опыта Резерфорда по рассеянию 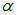— частиц

От радиоактивного источника, заключенного в свинцовый контейнер, 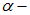частицы направлялись на тонкую фольгу Ф из исследуемого металла. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных 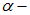частиц в опыте Резерфорда можно было проводить под различными углами 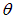к первоначальному направлению пучка. Было обнаружено, что большинство 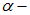частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие 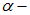частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 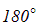. Очевидно, что 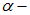частица может быть отброшена назад, только если положительный заряд атома и его масса сосредоточены в очень малом объеме внутри атома. Таким образом, было открыто атомное ядро — тело малых по сравнению с атомом размеров, в котором сосредоточен весь положительный заряд и практически вся его масса. Размеры ядра были оценены Э. Резерфордом в работе 1911 года, оценка дала меньше или порядка .

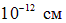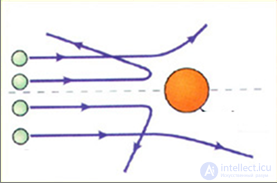
Рис. 3.13. Схема рассеяния альфа-частиц на ядре атома золота

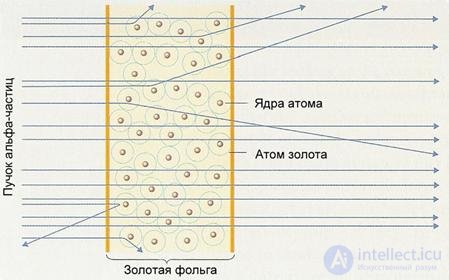
Рис. 3.14. Схема рассеяния потока альфа-частиц в тонкой золотой фольге

Возникла планетарная модель атома водорода: протон с электроном на орбите. Физики любят единые модели, а здесь так красиво в малом повторялось большое, в атоме — Солнечная система.

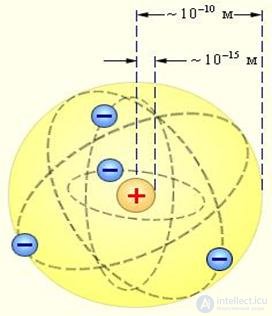
Рис. 3.15. Схема ядерной (планетарной) модели атома Резерфорда

Проблема состояла в том, что электрон, совершающий финитное, а следовательно — ускоренное движение около ядра, должен упасть на ядро. Дело в том, что электрон заряжен и при ускоренном движении должен испускать электромагнитное излучение, то есть стационарное движение невозможно. Классическая электродинамика предсказывает, что, быстро потеряв свою энергию и момент импульса орбитального движения, электрон должен упасть на ядро примерно за 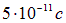. Свет за это время проходит около 1.5 см (получается, что мы видим лишь «мертвые» атомы, но это не так!). Резерфорд понимал проблему, но сознательно концентрировался на факте существования ядра, полагая, что вопрос об устойчивости атома будет решен при исследовании поведения атомных электронов. Это суждено было сделать в 1913 г. Н. Бору, предложившему новую теорию атома.

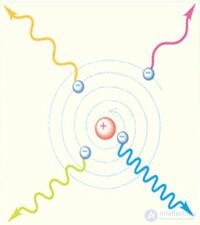
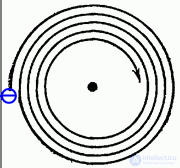
Рис. 3.16. Неустойчивость модели атома Резерфорда

Постулаты Бора

Первый постулат Бора

Здесь прослеживается «насильственное» введение дискретности (разрешены не все орбиты), а также типичное для физики «заметание проблемы под ковер»: если чему-то не находится объяснений, принимают это как данность и изучают следствия в надежде, что когда-нибудь поймут и причину.

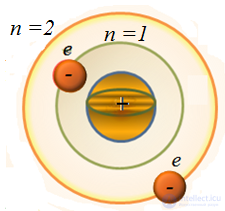
Рис. 3.17. Иллюстрация первому постулату Бора

Второй постулат Бора

Этот постулат отражает сохранение энергии и соотношение Планка – Эйнштейна.

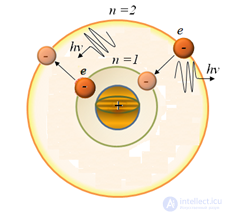
Рис. 3.18. Иллюстрация ко второму постулату Бора

Третий постулат Бора

Неизбежное следствие: так как остальные орбиты для электрона запрещены, переход осуществляется скачком; о пути и энергии электрона между орбитами говорить не имеет смысла: законы механики там не применимы.

Четвертый постулат Бора

Постоянная Планка ħ имеет размерность момента количества движения и вместе с зарядом электрона е и его массой m позволяет образовать параметр размерности длины. Это приводит к возможности вычислить размеры атома.

Рис. 3.19. Нильс Хе́нрик Дави́д Бор (1885–1962)

Применение постулатов Бора

Классическая механика для электрона, вращающегося по круговой орбите радиусом R со скоростью v вокруг ядра с зарядом Ze, дает уравнение движения

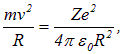
откуда

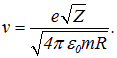
Поэтому энергия Е и момент импульса L электрона выражаются через радиус орбиты R:

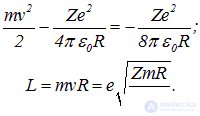
Если к последнему выражению применение условие квантования Бора L=nħ (n=1, 2, 3, …), то получатся следующие результаты.

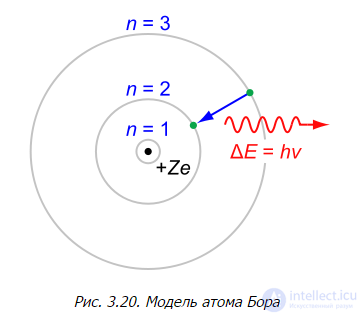
Рис. 3.20. Модель атома Бора

Характеристики водородоподобного атома

Радиусы разрешенных орбит

Энергия электрона на стационарной орбите

Константа а_В , имеющая размерность длины, называется радиусом Бора: 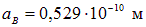. Смысл числа 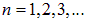— номер разрешенной орбиты. Радиус Бора — радиус низшей орбиты 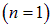в атоме водорода .

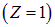Формула (3.3) определяет дискретные значения энергии, которые может иметь электрон в атоме водорода, или, как говорят, энергетические уровни. Отрицательные значения 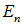соответствуют связанным состояниям электрона в атоме, то есть движениям в ограниченной области пространства (аналог в классической физике — движение планет по эллипсам в отличие от гиперболических и параболических траекторий, уходящих на бесконечность).

При решении задач о поведении электрона в атоме обычно возникают выражения, включающие квадрат электрического заряда электрона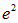 в комбинации с электрической постоянной 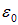. Весьма полезно ввести безразмерную комбинацию фундаментальных мировых постоянных — так называемую постоянную тонкой структуры:

которая, совместно с атомным номером 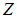и номером орбиты 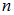, определяет масштаб релятивистских эффектов в атоме. Об этом говорит сайт https://intellect.icu . Для того, чтобы это было лучше видно, перепишем формулу (3.3) так, чтобы в ее правую часть входила постоянная тонкой структуры:

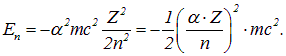
Из-за множителя 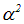характерные для атома энергии оказываются на четыре порядка меньше энергии покоя электрона. Это проявление нерелятивизма достаточно легких 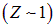атомных систем. Как видно из последнего выражения в приведенной выше формуле, релятивистские эффекты перестают быть малыми поправками для ближних к ядру 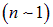электронов в тяжелых 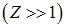атомах.

Пример 1. Определим скорость электрона на n-й орбите атома Бора. Радиус n-й орбиты определяется формулой

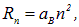
где а_В — радиус Бора. Скорость электрона v можно выразить через момент импульса L=nħ:

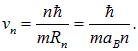
Выражение для радиуса Бора упростим, используя введенную постоянную тонкой структуры:

Подставляя это выражение в полученную выше формулу для скорости электрона, получаем для n-й орбиты

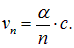
Отсюда вытекает, что на низшей орбите скорость электрона приблизительно в 137 раз меньше скорости света, то есть атом — действительно нерелятивистская система. На n – й орбите скорости электрона в n раз меньше, чем на первой. Численный пример: на второй орбите скорость электрона равна

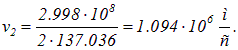
При переходе с уровня k на уровень 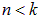излишек энергии 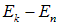перейдет в энергию фотона 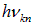. Поэтому для спектра излучаемых частот получаем соотношение (ср. (3.1))

Таким образом, теория Бора позволила также вычислить постоянную Ридберга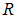. Стало понятно и существование спектральных серий, и предельных значений 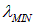(рис. 3.21).

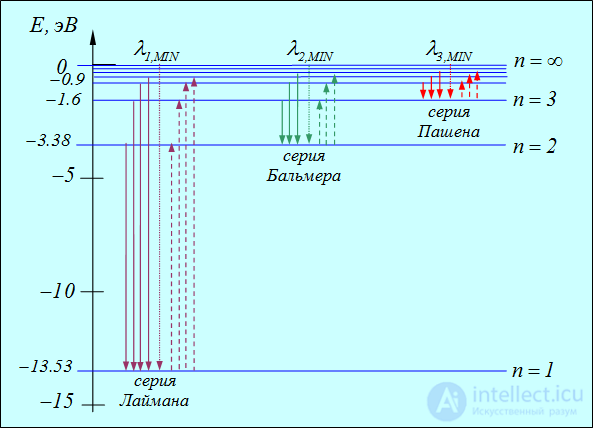
Рис. 3.21. Схема энергетических уровней и переходов в атоме водорода по теории Бора:
сплошные линии (переходы сверху вниз) — излучение, пунктирные линии (переходы снизу вверх) — поглощение.
Показаны границы (пределы) серий 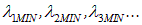, которым соответствуют переходы с уровня с
— границы между континуумом и дискретным спектром

Экспериментальное подтверждение утверждение Бора о дискретности энергетического спектра атомов нашло в опытах Франка — Герца, которые заключались в бомбардировке паров ртути электронами в вакуумной трубке и измерении зависимости анодного тока от ускоряющей разности потенциалов. Схема опыта приведена на рис. 3.22.

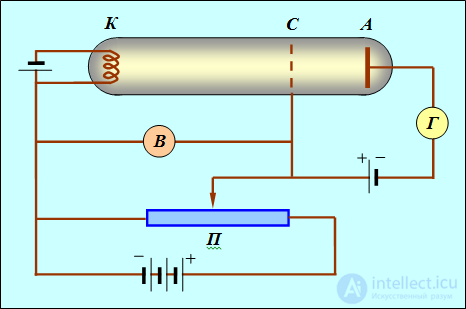
Рис. 3.22. Схема опыта Франка — Герца

В трубке, заполненной парами ртути под небольшим давлением (около 1 мм. рт. ст.), имеются три электрода: анод, катод и сетка. Электроны, вылетающие с поверхности подогретого катода вследствие термоэлектронной эмиссии, ускоряются напряжением U, приложенным между катодом и сеткой. Это напряжение можно менять с помощью потенциометра П. Между анодом и сеткой приложено слабое обратное поле с разностью потенциалов порядка 0,5ВВ , тормозящее движение электронов к аноду. Определялась зависимость тока I в цепи анода от приложенного напряжения U. Полученные результаты приведены на рис. 3.23.

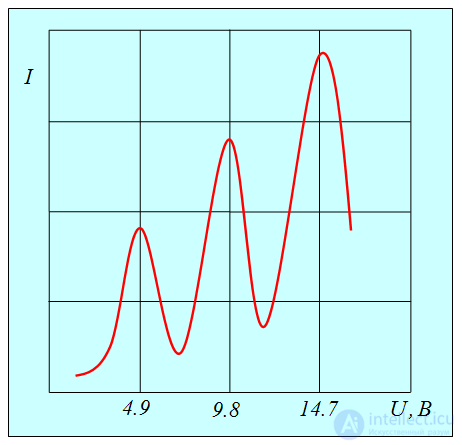
Рис. 3.23. Зависимость тока I в цепи анода от приложенного напряжения U в опыте Франка — Герца

Сила тока сначала монотонно возрастает, достигает максимума при напряжении 4,9 В, после чего с ростом U резко падает, достигает минимума и снова начинает расти. Максимумы силы тока повторяются при напряжениях 9,8 В, 14,7 В и т. д. Чередование максимумов на равном расстоянии друг от друга доказало дискретность изменения энергии атома.

Рис. 3.24. Неупругие столкновения электронов с атомами ртути

Рис. 3.25. Джеймс Франк (1882–1964)

Рис. 3.26. Гу́став Лю́двиг Герц (1887–1975)

Пример 2. При переходе с третьего уровня на второй (головная линия серии Бальмера) водородоподобный ион атома некоторого элемента испускает фотон с энергией 7,5 эВ. Определить, какой это элемент.

Энергия электрона, находящегося на n-ой орбите около ядра с зарядом Ze, равна

При переходе с уровня n на уровень выделяется энергия

откуда

Атомный номер элемента — целое число, так что после округления получаем Z = 2, что соответствует гелию.

Как отмечалось выше, еще до появления теории Бора был изучен спектр водородного атома и эмпирически установлена формула (3.1). Но при наблюдении спектра Солнца были замечены линии, казалось бы, нарушающие эту формулу, так как они соответствовали полуцелым значениям n и k. После появления теории Бора стало ясно, что квантовые числа n и k все-таки должны быть целыми, а кажущиеся полуцелые значения можно объяснить по-другому. Действительно, из формулы (3.6) для частот, испускаемых водородоподобным атомом, следует, что

то есть наблюдавшиеся линии принадлежат иону элемента с Z = 2. Как известно, этот элемент носит «солнечное» имя — гелий.

3.2. Волны материи

Итак, снова дискретность, таинственные целые числа. В классической физике они появлялись в явлениях интерференции (номера максимумов и минимумов) и в стоячих волнах (число узлов на струнах). В 1923 г. была выдвинута фундаментальная гипотеза Луи де Бройля:

Рис. 3.27. Луи Виктор Пьер Раймон, 7-й герцог Брольи, более известный как Луи де Бройль (1892–1987)

Фотону мы были вынуждены приписать импульс

Долгое время уделялось внимание только его волновым свойствам, а в XX в. восстановили в правах и корпускулярные. С электроном получилось наоборот: лишь де Бройль разглядел в нем колебания с длиной волны . Условие квантования Бора

получило простую интерпретацию. Оно стало условием того, чтобы на длине стационарной орбиты уложилось целое число длин волн:

(аналогия с обоями: если по периметру комнаты укладывается целое число периодов рисунка на обоях, то при дальнейшем оклеивании рисунок воспроизводится на тех же местах — своего рода стационарность). Отсюда вытекает соотношение

Видно, что получилась общая формула для фотонов и электронов (и любых других частиц).

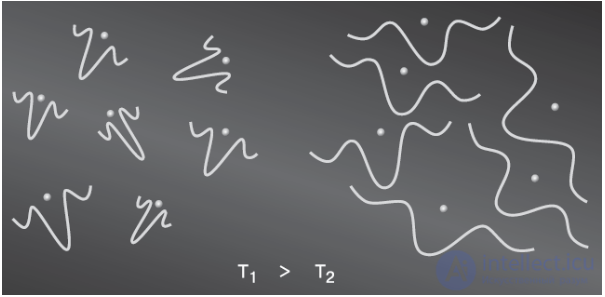
Рис. 3.28. Каждую частицу (атом, молекулу) можно представить в виде волны де Бройля или волнового пакета, центр которого соответствует центру частицы. По мере охлаждения, то есть снижения скорости хаотического движения частицы, длина волны растет, и волновые пакеты частиц в конце концов перекрываются. (Изображение: «Химия и жизнь»)

Гипотеза де Бройля подтверждена экспериментами Дэвиссона и Джермера (отражение от кристаллических плоскостей) и Томсона (дифракция на фольге). Красив и поучителен опыт В.А. Фабриканта (1949 г.) — дифракция одиночных электронов, доказывающая, что волновые свойства присущи не коллективу частиц, но каждому электрону в отдельности. И в то же время электрон — частица с зарядом и массой.

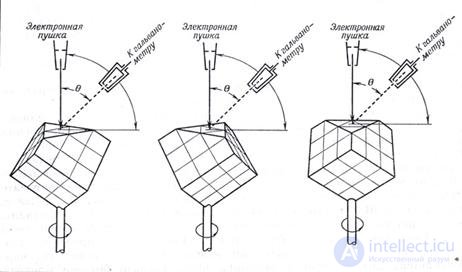
Рис. 3.29. Схема опыта Дэвиссона и Джермера по дифракции электронов (С. J. Davissоn, The discovery of electron waves, Les Prix Nobel en 1937.) На плоскость кристалла никеля, показанного в виде куба со срезанным углом, направляется пучок электронов определенной скорости. Цилиндр Фарадея, служащий для сбора дифрагированных электронов, может перемещаться по дуге вокруг кристалла. На рисунке изображены три различных положения кристалла

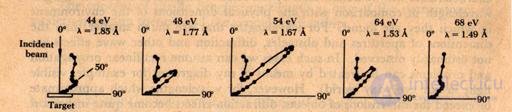
Рис. 3.30. Опыт Дэвиссона и Джермера по дифракции электронов. Полярные диаграммы интенсивности упруго рассеянных электронов для разных энергий первичного пучка

Рис. 3.31. Кли́нтон Джо́зеф Дэ́виссон (1881–1958)

Рис. 3.32. Лестер Хэлберт Джермер (1896–1971)

Рис. 3.33. Сэр Джозеф Джон Томсон (1856–1940)

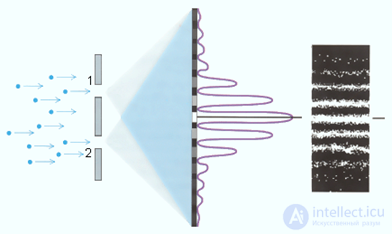
Рис. 3.34. Схема дифракции электронов на двух щелях

Рис. 3.35. Валенти́н Алекса́ндрович Фабрика́нт (1907–1991)

Вопрос, долго волновавший физиков: что такое микрочастица, волна или корпускула? Здесь налицо некорректная постановка вопроса, подразумевающая альтернативу. Надо «или» заменить на «и»: электрон и волна, и частица. Если задать этот вопрос природе с помощью прибора, то получим ответ, соответствующий прибору: для волнового прибора (например, дифракционной решетки) ответ будет «волна», для корпускулярного (скажем, счетчика) — «частица». Неоднозначность ответа отражает двойственность природы частиц или, точнее, узость нашего альтернативного мышления, допускающего лишь одну из этих возможностей. Это новые для нас объекты, квантовые русалки и кентавры микромира, которых невозможно разделить на людей и животных. В этом смысле микрообъект — не волна, не частица и не их симбиоз. Это новое качество, которое мы количественно отражаем в формуле де Бройля

связывающей волновые и корпускулярные проявления свойств единого объекта. В экспериментах с ускоренными частицами их длина волны де Бройля играет ту же роль, что и длина волны видимого света, определяющая разрешающую силу микроскопа. Ускорители — своеобразные микроскопы микромира, и с их помощью исследуются законы природы на малых расстояниях. Так, длина волны протонов, полученных на ускорителе в Серпухове, составляет примерно 10 ^–17 мм, что в 10 ⁷ раз меньше размеров атомов.

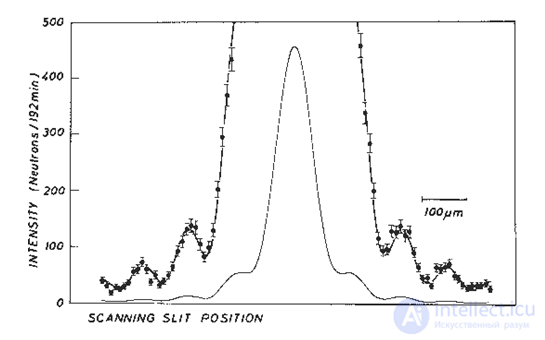
Рис. 3.36. Опыт с дифракцией нейтронов на щели шириной 90 мкм. Длина волны де Бройля для нейтронного пучка λ = 1,926 ± 0,07 ± 0,002 нм (средняя длина волны, разброс в пучке, ошибка измерения). Опыт занял около 320 часов, измерения проводились в течение двух недель на атомном реакторе с большим потоком нейтронов. На графике приведены общий вид зависимости, и она же увеличенном масштабе, чтобы лучше показать дифракционные максимумы более высокого порядка. Экспериментальные точки нанесены с указанием ошибок, сплошная кривая - результат теоретического расчета. С экспериментом согласуются и положение максимумов и их амплитуда. (Zeilinger et al. Rev. Mod. Phys., 1988, 60, 1067–1073)

При решении задач, связанных с длиной волны де Бройля, надо с осторожностью применять общую формулу (3.7). Необходимо ясно понимать, какое выражение для импульса следует использовать. Например, в задаче может быть задана скорость частицы v. Если эта скорость много меньше скорости света в вакууме, то можно применить классическое соотношение

На практике считают, что v<<с, если отношение v/c<0.3, то есть

Если же это не так, то следует применить релятивистское соотношение между импульсом частицы и ее скоростью

В задаче может быть задана не скорость частицы, а ее кинетическая энергия К. Критерием применимости классических формул является малость кинетической энергии по сравнению с энергией покоя частицы 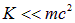. Если условие

выполняется (что, как нетрудно видеть, эквивалентно условию ), то для нахождения импульса можно воспользоваться формулами классической механики

откуда

Если же кинетическая энергия частицы не мала по сравнению с энергией покоя (тем более превышает ее), то следует использовать релятивистские формулы. В теории относительности выводится общее соотношение между полной энергией частицы и ее импульсом:

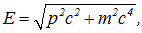
откуда

Кинетическая энергия равна разности между полной энергией и энергией покоя:

так что для импульса получаем

Наконец, удобно переписать это выражение так, чтобы под знаком квадратного корня стояли безразмерные величины:

Нетрудно убедиться, что при

формула (3.9) действительно переходит в классическое выражение

Традиционные единицы энергии (например, Дж) оказываются неудобными в микромире. Поэтому физики предпочитают пользоваться внесистемными единицами, с которыми мы уже встречались — электрон-вольтом (эВ) и его производными (1кэВ = 10³ эВ, 1МэВ = 10⁶ эВ , 1 ГэВ = 10⁹ эВ и т. п.).

Так как заряд электрона равен е = 1,602·10^–19Кл , то 1 эВ = 1,602·10^–19 Дж. Поскольку у нас появилась энергия покоя, приведем ее численные значения для электрона и протона вместе с массами этих частиц. Заодно укажем численные значения постоянной Планка, выраженной в эВ·с:

Наконец, встречаются обратные задачи, когда задана длина волны де Бройля l и требуется найти скорость или энергию частицы. Возникает вопрос, как по величине сразу определить, какими формулами следует пользоваться. Представим себе, что мы применяем для нахождения скорости классическую формулу

и, следовательно, получаем

Критерием справедливости этого результата является малость v по сравнению со скоростью света в вакууме c:

откуда

Комбинации констант

есть комптоновская длина волны частицы. По своему физическому смыслу это характерное расстояние, определяющее область , где уже неприменима нерелятивистская квантовая механика. Приведем численные значения этого важного параметра для электрона и протона:

Видно, что чем легче частица, тем больше ее комптоновская длина волны, то есть тем раньше проявятся релятивистские эффекты. Для электрона комптоновская длина волны много меньше характерной длины, определяющей размеры атома. Это значит, что к атому применима нерелятивистская квантовая механика. Ядра, состоящие из протонов и нейтронов, имеют размеры порядка 10^–14 мм, что много больше комптоновской длины волны протона. Следовательно, к ним также применима эта теория.

Рис. 3.37. Дифракционная картина, полученная при прохождении пучка электронов (E = 75 кВ, λ = 0,05 А) сквозь монокристаллическую пленку ZnSe с ориентацией (111)

Пример. Определим скорость частицы, у которой длина волны де Бройля в 10 раз меньше комптоновской длины волны .

По условию

откуда находим

Так как длина волны де Бройля меньше комптоновской длины волны частицы, то мы не можем воспользоваться нерелятивистским соотношением

которое приведет к несуразному ответу v=10с (как известно, ничто не может двигаться быстрее света). Здесь необходимо применить релятивистскую формулу связи импульса со скоростью

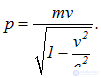
Отсюда вытекает уравнение

решение которого дает

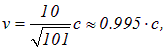
то есть скорость частицы всего на 0,5 % меньше скорости света.

3.3. Соотношения неопределенностей

Само наличие у частицы волновых свойств накладывает определенные ограничения на возможность корпускулярного описания ее поведения. Для классической частицы всегда можно указать ее точное положение и импульс. Для квантового объекта имеем иную ситуацию.

Представим цуг волн пространственной протяженностью — образ локализованного электрона, положение которого известно с точностью . Длину волны де Бройля для электрона можно определить, подсчитав число N пространственных периодов на отрезке :

Какова точность определения ? Ясно, что для слегка отличающейся длины волны мы получим примерно то же самое значение N. Неопределенность в длине волны ведет к неопределенности

в числе узлов, причем измерению доступны лишь . Так как

то отсюда немедленно следует знаменитое соотношение неопределенностей В. Гейзенберга для координат — импульсов (1927 г.):

Точности ради надо заметить, что, во-первых, величина в данном случае означает неопределенность проекции импульса на ось OX и, во-вторых, приведенное рассуждение имеет скорее качественный, нежели количественный характер, поскольку мы не дали строгой математической формулировки, что понимается под неопределенностью измерения. Обычно соотношение неопределенностей для координат-импульсов записывается в виде

Аналогичные соотношения справедливы для проекций радиуса-вектора и импульса частицы на две другие координатные оси:

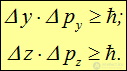
Представим теперь, что мы стоим на месте и мимо проходит электронная волна. Наблюдая за ней в течение времени , хотим найти ее частоту n. Насчитав колебаний, определяем частоту с точностью

откуда имеем

или (с учетом соотношения )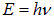

Аналогично неравенству (3.12) соотношение неопределенностей Гейзенберга для энергии системы чаще используется в виде

Рис. 3.38. Ве́рнер Карл Ге́йзенберг (1901–1976)

Поговорим о физическом смысле этих соотношений. Может сложиться представление, что в них проявляется «несовершенство» макроскопических приборов. Но приборы совсем не виноваты: ограничения носят принципиальный, а не технический характер. Сам микрообъект не может быть в таком состоянии, когда определенные значения одновременно имеют какая-то из его координат и проекция импульса на ту же ось.

Смысл второго соотношения: если микрообъект живет конечное время, то его энергия не имеет точного значения, она как бы размыта. Естественная ширина спектральных липни — прямое следствие формул Гейзенберга. На стационарной орбите электрон живет неограниченно долго и энергия определена точно. В этом — физический смысл понятия стационарного состояния. Если неопределенность в энергии электрона превышает разность энергий соседних состояний

то нельзя точно сказать, на каком уровне находится электрон. Иными словами, на короткое время порядка

электрон может перескочить с уровня 1 на уровень 2, не излучая фотона, и затем вернуться назад. Это — виртуальный процесс, который не наблюдается и, следовательно, не нарушает закона сохранения энергии.

Похожие соотношения существуют и для других пар так называемых канонически сопряженных динамических переменных. Так, при вращении частицы вокруг некоторой оси по орбите радиусом R неопределенность ее угловой координаты влечет за собой неопределенность ее положения на орбите . Из соотношений (3.12) следует, что неопределенность импульса частицы удовлетворяет неравенству

Учитывая связь момента импульса электрона L с его импульсом L = Rp, получаем , откуда следует еще одно соотношение неопределенностей

Некоторые следствия соотношений неопределенностей

Например, для осциллятора (тело на пружине) энергию Е можно записать в виде

Основное состояние в классической механике это состояние покоя в положении равновесия:

Поэтому величина неопределенностей и имеет порядок самих значений импульса и координаты, откуда получаем

Минимум энергии достигается в точке

и равен

Вообще говоря, такие оценки не могут претендовать на точный ответ, хотя в данном случае (как и для атома водорода) он действительно точен. Мы получили так называемые нулевые колебания: квантовый осциллятор, в отличие от классического, не может оставаться в покое — это противоречило бы соотношению неопределенностей Гейзенберга. Точные расчеты показывают, что формулу Планка для уровней энергии осциллятора надо было бы писать в виде

где n = 0, 1, 2, 3, ... — колебательное квантовое число.

При решении задач на применение соотношения неопределенностей следует иметь в виду, что в основном состоянии в классической физике электрон покоится в точке, соответствующей минимуму потенциальной энергии. Соотношения неопределенностей не позволяют ему это делать в квантовой теории, так что электрон должен иметь некоторый разброс импульсов. Поэтому неопределенность импульса (его отклонение от классического значения 0) и сам импульс по порядку величины совпадают

Неопределенность координаты электрона, «запертого» в объеме V, равна по порядку величины линейному размеру этого объема

Пример 1. Электрон с кинетической энергией находится в металлической пылинке диаметром . Оценим относительную неточность dv, с которой может быть определена скорость электрона.

По условию

и

Энергия электрона много меньше его энергии покоя, так что можно применять нерелятивистские соотношения

откуда

Для относительной неопределенности скорости электрона получаем

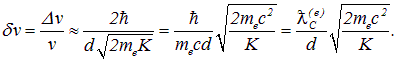
В этом выражении выделены безразмерные множители - отношение комптоновской длины волны электрона

к диаметру пылинки и отношение энергии покоя электрона к его кинетической энергии. Подставляем численные значения:

Пример 2. Среднее время жизни атома в возбужденном состоянии . При переходе в основное состояние излучается фотон с длиной волны (зеленый цвет). Определим энергию кванта, ширину и относительную ширину спектральной линии.

Энергия кванта равна

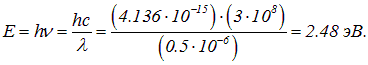
Неопределенность в энергии определяется по соотношению

откуда

Тогда

3.4. О границах применимости квантовой механики

Собственно, мы еще с квантовой механикой даже не познакомились, но лишь подошли к ее порогу. Тем не менее, уже сейчас можно дать оценку области, в которой заведомо не будут справедливы выводимые нами соотношения. Если подходить к микромиру со стороны области применимости классической физики, то никаких проблем не возникает. В самом деле, квантовые соотношения вовсе не отменяют классических законов, но уточняют их. В макромире, характеризуемом большими значениями энергий и моментов количества движения, квантовая дискретность просто незаметна, так что к макрообъектам можно, вообще говоря, применять и квантовые, и классические законы. Разница между получаемыми с их помощью количественными результатами будет ничтожно мала, но классические законы проще. В этом смысле мы говорим об области, где справедливы законы классической физики.

Иное дело, когда мы станем продвигаться вглубь микромира. Принципиально ясно, что где-то могут отказать и законы квантовой механики, и ученым придется придумывать какую-то новую теорию. В этом курсе мы будем заниматься нерелятивистской квантовой механикой изучающей микрообъекты, движущиеся со скоростями гораздо меньшими скорости света. Мы встретимся и с релятивистскими объектами (фотонами и др.), но будем оговаривать такие случаи особо.

Определим теперь область справедливости нерелятивистской квантовой механики. Представим себе микрочастицу с массой m. Квантовая неопределенность ее энергии должна быть много меньше энергии покоя

sup (в противном случае квантовые эффекты с необходимостью будут релятивистскими, что потребует обобщения теории). Из соотношения неопределенностей (3.13) и условия применимости нерелятивистских уравнений 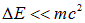следует ограничение на интервалы времени:

Характерное время

является, таким образом, водоразделом между релятивистской и нерелятивистской квантовыми теориями. За это время частица может пройти расстояние не больше

Величина l_C — характерное расстояние, на котором проходит граница между нерелятивистской и релятивистской теориями. Для электрона оно равно 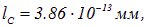а для протона — Соответствующие промежутки времени равны 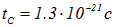для электрона и для протона.

На рис. 3.6 по оси х в логарифмическом масштабе отложены расстояния, а по оси у — скорости.

Рис. 3.39. Диаграмма расстояние — скорость для наглядной иллюстрации областей применимости физических теорий:
классической механики, специальной теории относительности (СТО), квантовой механики (КМ),
общей теории относительности (ОТО) и квантовой теории поля (КТП).
Точка показывает электрон в атоме — в сфере действия квантовой механики

Отмечены области применимости основных физических теорий (ОТО — общая теория относительности, СТО — специальная теория относительности, КМ — квантовая механика, КТП — квантовая теория поля, она же — релятивистская квантовая теория, она же — теория элементарных частиц). Границы между различными теориями размыты, так как они не отрицают друг друга, но развивают и дополняют. Так, КТП, занимающаяся свойствами элементарных частиц, родилась при соединении КМ и СТО, а ОТО (она же теория гравитации) — при распространении СТО и классической механики на область больших расстояний. Правая граница области КМ не означает, что квантовую механику нельзя применять там, где мы привыкли пользоваться классической. Просто это делать нецелесообразно. Обратим внимание, что рисунок ограничен с обеих сторон. Большой взрыв, в котором родилась наша Вселенная, произошел по современной оценке 14 миллиардов лет тому назад. За это время свет преодолел путь порядка 10²⁶ мм, что и определяет максимальные возможные расстояния в этом мире. На расстояниях порядка 10^–35 м необходимо учитывать силы гравитации, квантовая теория которых пока не создана. Только очень смелые теоретики решаются серьезно обсуждать, что происходит на столь малых расстояниях. Поэтому данная область на рисунке не показана.

Подведем итоги этой главы. Мы пришли к противоречивой картине микромира. В атоме Бора использовались законы движения по классической траектории, которые в результате оказались несправедливыми. Расчет радиуса орбиты и импульса электрона противоречит волновым идеям де Бройля, из которых мы и выводили эти характеристики. Наконец, совершенно непонятно, что же колеблется в пространстве при движении электрона?

Исследование, описанное в статье про волновые свойства микрочастиц, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое волновые свойства микрочастиц и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Атомная и Ядерная физика