7. Теплоемкость кристаллов. Квантовая статистика

Привет, Вы узнаете о том , что такое теплоемкость кристаллов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теплоемкость кристаллов, квантовая статистика , настоятельно рекомендую прочитать все из категории Атомная и Ядерная физика.

Мы завершаем свое знакомство со статистической физикой. Классическая статистика, математически выраженная распределением Максвелла Больцмана, подсчитывала число частиц, находящихся в малом объеме dV вокруг некой точки и имеющих импульсы в малом интервале вокруг некого значения 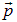. Познакомившись с законами квантовой механики, мы теперь понимаем, что для квантовых систем такой подход неприменим: микрочастицы не могут одновременно иметь определенные значения координаты и импульса, так что необходимо учесть соотношение неопределенностей Гейзенберга. Кроме того, мы уже знакомы с принципом Паули, согласно которому электроны «мешают» друг другу и не могут занять одно и то же состояние. Очевидно, что это также должно найти отражение в квантовой статистике, знакомству с которой посвящена настоящая глава. Первое и почти очевидное применение квантовая статистика нашла в теории теплоемкости твердых тел. Мы коснемся также интереснейших макроскопических квантовых явлений — сверхтекучести и сверхпроводимости.

7.1. Классические представления о модели кристалла

Простейшей моделью кристалла является геометрически правильно построенная кристаллическая решетка, в узлах которой помещаются атомы, которые считаются материальными точками. Атомы совершают тепловые колебания около положений равновесия. Если колебания малы, то их можно считать гармоническими. Энергия каждого атома складывается из кинетической и потенциальной энергий. На каждую степень свободы приходится в среднем кинетическая энергия

и такая же величина средней потенциальной энергии. Таким образом, среднее значение полной энергии, приходящейся на одну колебательную степень свободы, равно:

.

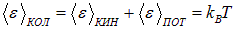Напомним теперь классические результаты для теплоемкости кристаллической решетки, о которых говорилось ранее. Предположим для простоты, что все атомы одинаковы и каждый из них обладает тремя колебательными степенями свободы, а потому на него приходится средняя энергия 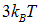. Умножив эту величину на постоянную Авогадро , можно получить внутреннюю энергию одного моля кристаллического твердого тела:

где R — универсальная газовая постоянная. Отсюда для молярной теплоемкости твердого тела имеем

Этот закон был установлен в 1819 г. П. Дюлонгом и А. Пти как эмпирическое правило, согласно которому произведение удельной теплоемкости химического элемента в твердом состоянии на его атомную массу (молярная теплоемкость) примерно одинаково для всех элементов и равно

.

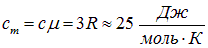Если вещество кристалла состоит из молекул, имеющих атомов, то закон Дюлонга и Пти модифицируется очевидным образом:

(так, например, для молекул поваренной соли NaCl ).

Недостатки классической теории теплоемкости

1. Классическая теория не дает объяснения зависимости теплоемкости тел от температуры. Экспериментально установлено, что при приближении к абсолютному нулю теплоемкости и всех тел, в том числе и кристаллов, стремятся к нулю.

2. По теореме о равномерном распределении энергии все степени свободы равноправны. Однако опыт приводит к заключению, что при низких температурах вклад в теплоемкость вносят не все из них: при понижении температуры определенные степени свободы становятся малоэффективными (говорят, что они «заморожены»). Так, при температуре

«замерзают» колебательные степени свободы (здесь — частота осциллятора). Совершенно аналогично из-за квантования энергии вращения «замерзают» вращательные степени свободы: это происходит при

где I — момент инерции молекулы.

3. Закон Дюлонга и Пти был сформулирован для любого твердого тела: металла и диэлектрика. Однако металл состоит из положительно заряженных ионов, совершающих тепловые колебания вокруг узлов кристаллической решетки. Между ними движутся так называемые «свободные» электроны, которые ведут себя подобно электронному газу. Наличием свободных электронов объясняется высокая электрическая проводимость металлов. Классическая теория теплоемкости не принимает во внимание наличие электронного газа в металлах. Она учитывает только тепловые колебания ионов и приводит к результату Дюлонга и Пти. В отличие от диэлектриков, в металлах следовало бы учесть вклад в теплоемкость, вносимый электронами. На каждый свободный электрон приходится средняя кинетическая энергия

.

Поэтому по классической теории теплоемкость электронного газа должна быть сравнимой с теплоемкостью кристаллической решетки. Опыт показывает, что свободные электроны практически не вносят никакого вклада в теплоемкость металлов.

7.2. Квантовая теория теплоемкости Эйнштейна

Квантовая теория устранила трудности, на которые натолкнулась классическая теория в вопросе теплоемкости твердых тел. Представим тело как систему N осцилляторов, не взаимодействующих друг с другом. Применим к этой системе закон распределения Больцмана, учитывая, что энергия гармонического осциллятора квантуется:

Если обозначить число осцилляторов с квантовым числом n, причем

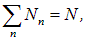
то средняя энергия, приходящаяся на одну молекулу в состоянии термодинамического равновесия, определяется выражением

Согласно распределению Больцмана, вероятность найти осциллятор в состоянии с квантовым числом 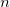равна

Подставляя соотношения (7.5) и (7.3) для и в формулу (7.4) и выполняя суммирование, приходим к выражению для средней энергии гармонического осциллятора:

Формула (7.6) отличается от полученного ранее выражения наличием дополнительного первого слагаемого.

Это слагаемое

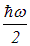
есть энергия «нулевых колебаний» гармонического осциллятора, которая не зависит от температуры и потому не вносит вклада в теплоемкость системы.

Выражение (7.6) было положено Эйнштейном в основу квантовой теории теплоемкости твердых тел. Эйнштейн отождествил кристаллическую решетку из N молекул с системой независимых гармонических осцилляторов с одинаковой собственной частотой w. Тогда внутренняя энергия одного моля определяется выражением

.

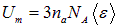Дифференцируя его по температуре, получаем молярную теплоемкость кристаллической решетки твердых тел

Это и есть формула Эйнштейна для теплоемкости кристаллов. При высоких температурах, когда

она переходит в классическую формулу

.

В другом предельном случае низких температур, когда

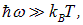
можно пренебречь единицей в знаменателе и получить

При T, стремящемся к 0, полученное выражение стремится к нулю, как это требует тепловая теорема Нернста (см. разд. 5.7).

Поясним физический смысл этого результата. Из-за квантовой дискретности между основным и возбужденным уровнями системы осцилляторов имеется конечный энергетический зазор (энергетическая щель). Меньшее количество энергии осциллятор воспринять просто не в состоянии. При нулевой температуре в системе нет возбуждений — все осцилляторы находятся в основном состоянии. При небольшом повышении температуры тепловой энергии не хватает на преодоление этой щели, и лишь малое количество осцилляторов, пропорциональное

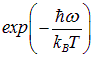
согласно закону Больцмана переходит на первый возбужденный уровень. Именно они ответственны за поглощение тепловой энергии и, соответственно, за малую теплоемкость кристалла при низких температурах. При высоких температурах тепловой энергии хватает на возбуждение многих вышележащих колебательных уровней, так что дискретность энергии уже не играет особой роли — мы возвращаемся к классическому результату Дюлонга и Пти.

Однако согласие с опытом теории Эйнштейна имеет только качественный характер. В выражении для при низких температурах экспоненциальный множитель убывает быстрее, чем растет множитель . Поэтому при приближении к абсолютному нулю теплоемкость стремится к нулю практически по экспоненциальному закону. Опыт же показывает, что теплоемкость кристаллов изменяется при низких температурах не экспоненциально, а по степенному закону

.

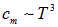Как оказалось, эти расхождения теории Эйнштейна с опытом связаны не с существом квантовой теории, а с упрощением расчета, в котором предполагалось, что все гармонические осцилляторы колеблются с одной и той же частотой. На самом деле кристаллическую решетку следует рассматривать как связанную систему взаимодействующих частиц. При вычислении теплоемкости тело действительно можно рассматривать как систему гармонических осцилляторов, но с различными частотами. Задача сводится к отысканию спектра частот.

7.3. Теория теплоемкости твердых тел Дебая

П. Дебай учел, что колебания атомов в кристаллической решетке не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных между собой атомов, обладающих 3N степенями свободы. Каждая степень свободы (нормальное колебание) может быть представлена как гармонический осциллятор, среднюю энергию которого мы уже вычислили (см. (7.6)). Из-за связи между атомами частоты нормальных колебаний уже не совпадают между собой. Взаимодействие атомов приводит к тому, что колебание, возникшее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Эта волна, дойдя до границы кристалла, отражается. При наложении прямой и отраженной волн образуется стоячая волна, которой соответствует некоторое нормальное колебание кристаллической решетки. Число dN нормальных колебаний, то есть стоячих волн, в интервале частот от 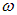до велико, поэтому суммирование в выражении для внутренней энергии системы может быть заменено интегрированием:

Число колебаний в единице объема. В этом разделе мы займемся подсчетом числа стоячих волн, имеющих близкие частоты 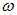. В сущности, мы проделали уже эти выкладки ранее для электромагнитного излучения, но повторим их снова с небольшими модификациями для применения также и к упругим колебаниям в кристалле.

Рассмотрим сначала одномерный потенциальный ящик длиной . Мы могли уже убедиться, что стоячая волна в нем (неважно, электромагнитная ли, звуковая или волна де Бройля), описывается функцией sin(kx), которая должна обращаться в нуль на границах ящика. Отсюда

Число 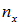нумерует различные стоячие волны вдоль оси х, и потому на малый интервал волнового вектора приходится число колебаний

Двойку в знаменателе мы поставили, чтобы избежать двойного счета: заме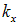на на приводит к той же стоячей волне. В трехмерном ящике для волн, распространяющихся по другим осям, получаем аналогичные формулы

Перемножая (7.11) и (7.12), находим для полного числа стоячих волн в ящике объемом

Наконец, учтем, что каждой стоячей волне может соответствовать g поляризаций (например, для волн де Бройля, соответствующих частицам со спином s, имеем g = 2s + 1 — число различных проекций спина). Окончательно имеем

Формула (7.14) дает число различных стоячих волн (отличающихся числом узлов и направлениями поляризации) в объеме V, приходящихся на элемент объема в пространстве волнового вектора 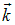. Далее, для перехода к частотам волн вспомним соотношение

где v — фазовая скорость волны. Отсюда

.

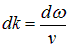и окончательно получаем

Мы вывели формулу (7.15) для прямоугольного объема, но можно показать, что форма объема не влияет на результат. Не имеет большого значения и физическая природа колебаний, число которых мы подсчитали. Например, для фотонов v = c и g = 2 (свет может иметь правую и левую циркулярные поляризации). В итоге получаем уже известную нам формулу для числа типов фотонов в объеме V с частотой в интервале :

Для применения (7.15) к звуковым волнам в кристалле учтем, что там возможна одна продольная волна, распространяющаяся со скоростью , и две поперечные волны с разными поляризациями, как у фотонов, распространяющиеся со скоростью 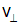. Теперь очевидно, как обобщить формулу (7.15) на данный случай:

Здесь мы ввели величину v, играющую роль некого среднего между скоростями продольных и поперечных волн; она вычисляется из соотношения

Характеристическая температура Дебая. Подставляя (7.17) и (7.6) в выражение (7.9) для внутренней энергии, получаем

где 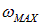— максимальная частота нормальных колебаний, которая определяется из нормировочного соотношения

так как полное число нормальных колебаний равно числу степеней свободы. Используя (7.17), находим

где n — концентрация атомов (их число в единице объема кристалла). Таким образом, максимальная частота нормальных колебаний, называемая дебаевской частотой, равна

Следует отметить, что наименьшая длина упругой волны в кристалле, которая соответствует максимальной частоте , равна

где

.

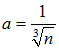— расстояние между соседними атомами в кристаллической решетке. Этот результат согласуется с тем, что волны, длины которых меньше удвоенного межатомного расстояния, не могут существовать в кристалле.

Используя определение (7.22) и учитывая, что для одного моля кристалла концентрация атомов равна

где — число атомов в

продолжение следует...

Продолжение:

Часть 1 7. Теплоемкость кристаллов. Квантовая статистика
Часть 2 7.4. Фононы - 7. Теплоемкость кристаллов. Квантовая статистика
Часть 3 7.7. Статистика Бозе — Эйнштейна - 7. Теплоемкость кристаллов. Квантовая
Часть 4 - 7. Теплоемкость кристаллов. Квантовая статистика