Лекция
Это продолжение увлекательной статьи про теплоемкость кристаллов.
...
молекуле вещества кристалла, мы можем записать внутреннюю энергию одного моля в виде
|
|
|
(7.24) |
Дифференцируя внутреннюю энергию U по температуре, можно получить молярную теплоемкость кристалла:
|
|
|
(7.25) |
Введем новый параметр — характеристическую температуру Дебая
|
|
|
(7.26) |
и выполним в интеграле (7.25) замену переменных
 .
.
Тогда молярную теплоемкость кристалла можно записать в виде
|
|
|
(7.27) |
При низких температурах 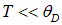 верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Тогда интеграл будет представлять собой число
верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Тогда интеграл будет представлять собой число
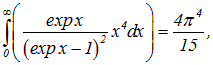
и теплоемкость окажется пропорциональной кубу температуры:
|
|
|
(7.28) |
Эта приближенная зависимость известна как закон Дебая и хорошо согласуется с экспериментом при достаточно низких температурах 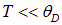 .
.
При высоких температурах 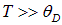 экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора:
экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора:
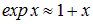 .
.
Тогда для молярной теплоемкости получается значение
|
|
|
(7.29) |
то есть закон Дюлонга и Пти.
О согласии теории Дебая с опытом можно судить по графику рис. Об этом говорит сайт https://intellect.icu . 7.1, на котором показаны экспериментальные точки для некоторых веществ.
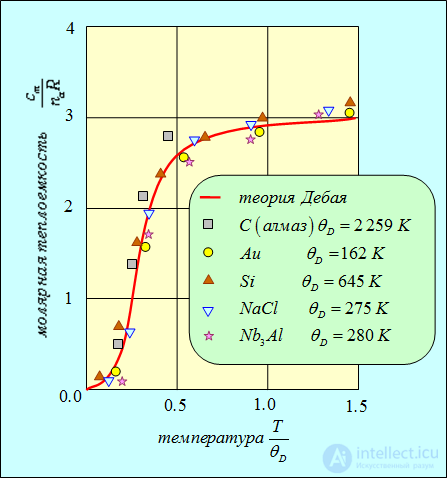
Рис. 7.1. Сравнение теории теплоемкости Дебая с экспериментальными данными: показаны вещества с заметно различающимися значениями дебаевской температуры и разным составом молекул ( для NaCl и
для NaCl и 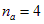 для
для 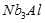 ), но все точки лежат достаточно близко от теоретической кривой
), но все точки лежат достаточно близко от теоретической кривой
Пример. Пользуясь данными, приведенными на графике рис. 7.1, найдем максимальную частоту колебаний 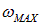 в кристалле золота по теории Дебая.
в кристалле золота по теории Дебая.
Температура Дебая для золота, как указано на графике, равна 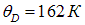 . Используя (7.26), находим
. Используя (7.26), находим

Как и внутри молекул, атомы в кристалле совершают малые колебания около фиксированных положений равновесия. Колебания атомов распространяются по кристаллу в виде слабо взаимодействующих волн с волновыми векторами  и частотами
и частотами  . Физически нормальные колебания в кристаллах порождают волны деформации кристаллической решетки (то есть упругие волны). Таким образом, движение атомов в кристалле может быть описано как суперпозиция плоских волн различной частоты
. Физически нормальные колебания в кристаллах порождают волны деформации кристаллической решетки (то есть упругие волны). Таким образом, движение атомов в кристалле может быть описано как суперпозиция плоских волн различной частоты
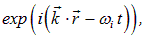
каждой из которых соответствует гармонический осциллятор с частотой  .
.
Следуя идеям де Бройля, такой упругой волне в кристалле можно сопоставить квазичастицу с энергией
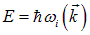
и импульсом
 .
.
Она носит название фонона.
|
Фонон — элементарная порция звуковой энергии, подобно тому как фотон — элементарная порция световой (электромагнитной) энергии. |
Наше сопоставление можно схематически изобразить следующим образом:

Индекс i стоит для обозначения типа соответствующей волны (продольная, поперечная, характеризующаяся определенным законом дисперсии

и т. п.), или, как говорят, фононной моды. При квантово-механическом рассмотрении гармонический осциллятор данной фононной моды, как мы уже знаем, может иметь энергию
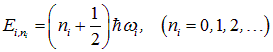 .
.
При 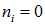 мы имеем нулевые колебания с энергией
мы имеем нулевые колебания с энергией
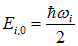
— фонона данной моды в твердом теле нет. При  мы имеем новое состояние с энергией возбуждения
мы имеем новое состояние с энергией возбуждения
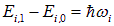
— это и есть квазичастица фонон. При произвольном квантовом числе ni энергия возбуждения равна
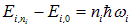 .
.
В таком случае мы говорим, что в твердом теле распространяются i фононов данной моды i.
Используя полученные выше результаты, в случае термодинамического (теплового) равновесия можно найти среднее число фононов 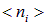 с частотой
с частотой 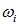 . Действительно, мы уже нашли среднюю энергию
. Действительно, мы уже нашли среднюю энергию 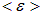 квантового осциллятора (см. (7.6), где частоту
квантового осциллятора (см. (7.6), где частоту 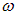 надо заменить теперь на частоту упругой волны
надо заменить теперь на частоту упругой волны 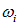 ). С другой стороны, эту же энергию можно представить в виде (7.6)
). С другой стороны, эту же энергию можно представить в виде (7.6)
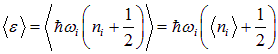 .
.
Приравнивая эти выражения, получаем
|
|
|
(7.30) |
При низких температурах
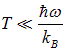
среднее число фононов экспоненциально убывает при T, стремящемся к 0: в системе не возникает возбуждений. Наоборот, при высоких температурах

экспоненту в знаменателе можно разложить в ряд Тейлора и получить результат
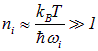 .
.
Следовательно, из полученного соотношения вытекает, что при достаточно высокой температуре в кристалле может одновременно возбуждаться неограниченное количество одинаковых фононов, то есть принцип Паули на фононы не распространяется. Напомним, что кванты электромагнитного поля — фотоны, находящиеся в состоянии равновесия со стенками полости, также подчиняются этому распределению.
Представление о фононах широко используется в физике твердого тела. Фононы называют квазичастицами, поскольку они хотя и вполне реальны, но существуют только в кристаллах: вне среды их нет. Идея существования квазичастиц была впервые выдвинута Л.Д. Ландау в 40-х годах прошлого века. Кроме фононов есть и другие типы квазичастиц. Тепловые колебания решетки можно рассматривать как фононный газ, при низких температурах — идеальный. При очень высоких температурах решетка плавится и модель невзаимодействующих фононов неприменима: они перестают быть свободными. Преимущество представления о фононах состоит в том, что в его рамках свойства твердого тела рассматриваются как свойства ансамбля большого числа независимых квазичастиц — фононного газа. Все представления этой модели могут быть использованы для описания поведения кристаллической решетки.
Можно рассматривать также взаимодействие обычных частиц (электронов, фотонов) с фононами. Так, электроны, обмениваясь фононами, испытывают притяжение. Несмотря на кулоновское отталкивание, может даже образоваться связанное состояние пары электронов. Подобный механизм ведет к явлению сверхпроводимости (будет рассмотрено далее).
Ранее мы обсуждали комбинационное рассеяние света кристаллами. Этот процесс можно трактовать как процесс взаимодействия фотона с газом фононов. Фотон, пролетающий через кристаллическую решетку, может возбудить в ней фонон одной из частот оптической моды кристалла. При этом фотон полностью поглощается кристаллической решеткой, потом излучается новый фотон, но уже с меньшей энергией, так часть энергии остается в кристаллической решетке в виде рожденного в ней фонона — возникает красный спутник: фотон с меньшей энергией. Если в кристалле уже был возбужден фонон, то возможен и обратный обмен энергией: пролетающий фотон, в результате поглощения и нового рождения может увеличить свою энергию за счет энергии фонона; в таком случае возникает фиолетовый спутник: фотон с большей энергией.
Мы уже убедились, что число фононов в твердом теле не постоянно. Фононов тем больше, чем интенсивнее тепловое движение атомов, то есть чем выше температура. При высоких температурах число фононов пропорционально температуре, а с приближением к абсолютному нулю их число стремится к нулю экспоненциально.
Две частицы тождественны, если все их физические свойства в точности совпадают, что исключает возможность экспериментально различать их. В классической теории всегда предполагается, что мы можем в принципе проследить за движением частиц и сказать, какая из них куда полетела. Поэтому в классической теории даже тождественные частицы в принципе различимы. В квантовой механике это не так: принцип неопределенности не позволяет прослеживать траектории и, стало быть, неразличимость частиц имеет принципиальный характер и влияет на результат вычислений.
Пусть, например, система из двух частиц описывается гамильтонианом (оператором энергии)

и пусть система находится в состоянии с волновой функцией
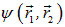 .
.
Введем оператор
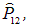
переставляющий частицы местами, то есть обменивающий их радиусы-векторы:
|
|
|
(7.31) |
Математически тождественность частиц выражается в инвариантности (неизменности) гамильтониана относительно операции перестановки
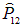
этих частиц, что в квантовой механике записывается как условие коммутации операторов

то есть
|
|
|
(7.32) |
Это условие обеспечивает физическую неразличимость частиц, поскольку тогда волновая функция  будет также решением уравнения Шредингера с тем же значением энергии. Действительно, если
будет также решением уравнения Шредингера с тем же значением энергии. Действительно, если

и мы подействуем на обе части этого уравнения оператором коммутации

то получим
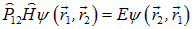 .
.
Из-за условия коммутации мы можем пронести оператор коммутации через гамильтониан:
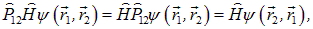
и наше уравнение примет вид
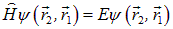 .
.
Но мы помним, что коммутирование операторов с гамильтонианом означает сохранение их собственных значений. Найдем собственные значения р оператора коммутации. Для этого надо решить уравнение
|
|
|
(7.33) |
С учетом определения (7.31) оператора коммутации, записываем это уравнение в виде
|
|
|
(7.34) |
Снова подействуем на обе части (7.34) оператором перестановки частиц:
|
|
|
(7.35) |
Из (7.34) и (7.35) получаем, что
|
|
|
(7.36) |
то есть 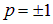 . Таким образом, оператор коммутации может иметь только два собственных значения. При p = 1 волновая функция симметрична относительно операции перестановки частиц:
. Таким образом, оператор коммутации может иметь только два собственных значения. При p = 1 волновая функция симметрична относительно операции перестановки частиц:
 .
.
При p = –1 имеем антисимметричную волновую функцию:
 .
.
Таким образом, мы получили важный результат:
|
Волновые функции системы двух тождественных частиц могут быть либо четными, либо нечетными относительно операции перестановки частиц местами. |
Справедливо обобщение этого результата:
|
Состояния системы тождественных частиц либо симметричны, либо антисимметричны относительно перестановки любых двух из них. |
Какое состояние реализуется — зависит от природы рассматриваемых частиц.
|
Частицы с симметричными состояниями называются бозонами, с антисимметричными — фермионами. |
Ранее этими именами мы называли частицы с целым и полуцелым спинами, соответственно. В релятивистском уравнении Дирака, в отличиe от уравнения Шредингера, спин частиц возникает автоматически. Существует фундаментальная теорема Паули:
|
Частицы с полуцелым спином (s = 1/2, 3/2 и т. д.) описываются антисимметричными волновыми функциями, а с целым (s = 0, 1, 2 и т. д.) — симметричными. |
Эта теорема о связи спина со статистикой является следствием объединения квантовой механики с теорией относительности.
Обратимся для примера к состоянию двух атомных электронов. В пренебрежении взаимодействием между ними волновая функция распадается на произведение волновых функций каждого электрона по отдельности:
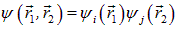 .
.
Индексы i, j обозначают здесь полный набор квантовых чисел (n, l, m, s), которыми одно состояние отличается от другого. Меняя электроны местами, приходим к состоянию с той же энергией, описываемому волновой функцией
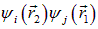 .
.
Поэтому в силу принципа суперпозиции возможны состояния, описываемые любой линейной комбинацией этих двух функций, причем все они будут иметь ту же энергию. Однако мы теперь знаем, что для электронов со спином s = 1/2 физический смысл имеет лишь антисимметричная комбинация
|
|
|
(7.37) |
Если состояния электронов одинаковы (i = j, то есть совпадают все квантовые числа), то
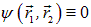 .
.
Мы снова пришли к принципу Паули:
|
Не может быть двух электронов в одном состоянии.
|
Бозоны и фермионы имеют совершенно разные статистические свойства, то есть по-разному ведут себя в коллективе себе подобных. Кроме непосредственного силового взаимодействия между частицами, имеется специфически квантовое, обменное взаимодействие: это не какие-то дополнительные силы или поля — одни частицы влияют на поведение других одним своим присутствием. Эти эффекты ощущаются частицами, если они находятся друг от друга на расстояниях, меньших или порядка длины волны де Бройля  . При высоких температурах энергии частиц велики и
. При высоких температурах энергии частиц велики и 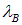 мало — это область классической физики. При низких температурах
мало — это область классической физики. При низких температурах  возрастает и квантовые эффекты доминируют.
возрастает и квантовые эффекты доминируют.
Рассмотрим систему одинаковых фермионов с энергиями  в состоянии i (где i обозначает набор квантовых чисел, включая спин). Обозначим через
в состоянии i (где i обозначает набор квантовых чисел, включая спин). Обозначим через  число частиц в состоянии i. Основной принцип статистической физики (классической и квантовой) формулируется исследующим образом:
число частиц в состоянии i. Основной принцип статистической физики (классической и квантовой) формулируется исследующим образом:
|
Вероятность обнаружить систему в состояния i равна
|
Здесь C — нормировочная постоянная, а 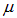 — химический потенциал. Этот параметр появляется всегда при фиксированном числе частиц в системе, которое равно
— химический потенциал. Этот параметр появляется всегда при фиксированном числе частиц в системе, которое равно
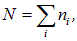
где сумма берется по всем состояниям. По сути дела, уравнение (7.38) — это обобщение известного распределения Больцмана. Из принципа Паули следует, что для фермионов  могут принимать лишь значения 0 и 1 — в данном состоянии i может быть либо одна частица, либо ни одной вообще.
могут принимать лишь значения 0 и 1 — в данном состоянии i может быть либо одна частица, либо ни одной вообще.
Из всего набора возможных состояний системы проследим за каким-то конкретным состоянием k с энергией 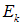 . С некой вероятностью
. С некой вероятностью
|
|
|
(7.39) |
в нем может не оказаться ни одной частицы (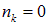 ). С вероятностью
). С вероятностью
|
|
|
(7.40) |
в нем окажется одна частица (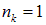 ). При записи формул (7.39), (7.40) мы использовали общее выражение (7.38) для вероятности
). При записи формул (7.39), (7.40) мы использовали общее выражение (7.38) для вероятности
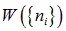 .
.
Поскольку третьего не дано, должно выполняться условие нормировки
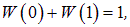
откуда следует
|
|
|
продолжение следует...
Часть 1 7. Теплоемкость кристаллов. Квантовая статистика
Часть 2 7.4. Фононы - 7. Теплоемкость кристаллов. Квантовая статистика
Часть 3 7.7. Статистика Бозе — Эйнштейна - 7. Теплоемкость кристаллов. Квантовая
Часть 4 - 7. Теплоемкость кристаллов. Квантовая статистика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика