Лекция
Это окончание невероятной информации про теплоемкость кристаллов.
...
энергией  . Оказалось, что первостепенную роль играет закон зависимости энергии от импульса
. Оказалось, что первостепенную роль играет закон зависимости энергии от импульса 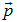 — закон дисперсии. В квантовой бозе-жидкости «возбуждения» (квазичастицы) — также бозоны с нулевым спином. При низких температурах число квазичастиц мало, и их можно считать невзаимодействующими. В этом случае имеем идеальный газ квазичастиц, который при какой-то критической температуре испытывает конденсацию.
— закон дисперсии. В квантовой бозе-жидкости «возбуждения» (квазичастицы) — также бозоны с нулевым спином. При низких температурах число квазичастиц мало, и их можно считать невзаимодействующими. В этом случае имеем идеальный газ квазичастиц, который при какой-то критической температуре испытывает конденсацию.
Но все, повторим, зависит от закона дисперсии, полный расчет которого очень сложен и до сих пор не выполнен. Боголюбов вычислил дисперсию слабовозбужденных состояний. В предельных случаях его формула дает
|
|
|
(12) |
где v — некая постоянная с размерностью скорости. Энергия в первом случае есть не что иное, как энергия атома гелия. Энергия же во втором предельном случае аналогична энергии акустического кванта (фонона). Ход кривой показан на рис. 3.
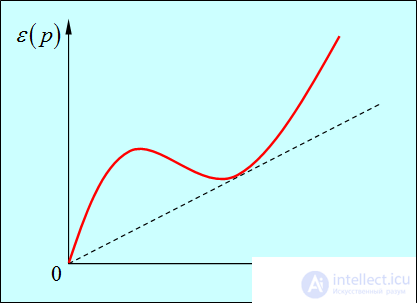
Рис. 3. Зависимость энергии квазичастиц в Не II от их импульса (закон дисперсии)
Таким образом, при T > 0 жидкий гелий состоит из конденсата квазичастиц и идеального газа квазичастиц с энергией 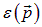 . Атомы гелия нельзя разделить на «образующие конденсат» и «порождающие свободные квазичастицы»: все они принимают участие в образовании как основного конденсатного состояния, так и идеального газа. Газ квазичастиц может рассматриваться как нормальный компонент жидкого гелия, а конденсат — как сверхтекучий. Подобная феноменологическая теория двухкомпонентной жидкости была развита Ландау (1941).
. Атомы гелия нельзя разделить на «образующие конденсат» и «порождающие свободные квазичастицы»: все они принимают участие в образовании как основного конденсатного состояния, так и идеального газа. Газ квазичастиц может рассматриваться как нормальный компонент жидкого гелия, а конденсат — как сверхтекучий. Подобная феноменологическая теория двухкомпонентной жидкости была развита Ландау (1941).
Сверхтекучесть конденсата. Мы разобрались, почему в жидкости может появиться идеальный газ: свободные частицы газа — это не сами атомы гелия, но возбуждения основного состояния (конденсата). Теперь надо понять происхождение сверхтекучести конденсата.
Сначала напомним результаты классической механики, касающиеся перехода к движущимся системам отсчета. Пусть дана система K, в которой радиус-векторы частиц с массами 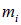 обозначены
обозначены 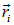 . Импульс такой системы есть
. Импульс такой системы есть
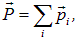
а кинетическая энергия
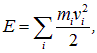
где
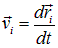 .
.
Пусть дана также система 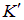 , положение начала координат которой задается вектором
, положение начала координат которой задается вектором 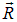 , скорость системы
, скорость системы  относительно K есть
относительно K есть
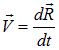 .
.
В движущейся системе координат радиус-векторы частиц есть
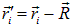 .
.
Отсюда немедленно следуют выражения для полного импульса и энергии частиц в движущейся системе координат (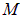 — полная масса всех частиц):
— полная масса всех частиц):
|
|
|
(13) |
Это нерелятивистские преобразования Галилея, известные из классической механики. Следуя рассуждениям Ландау, применим теперь эти формулы к невозбужденному конденсату, текущему по трубке со скоростью  . В лабораторной системе отсчета K энергия и импульс конденсата даются очевидными формулами
. В лабораторной системе отсчета K энергия и импульс конденсата даются очевидными формулами
|
|
|
(14) |
где 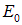 — энергия покоящегося конденсата в основном состоянии. Возьмем систему
— энергия покоящегося конденсата в основном состоянии. Возьмем систему 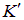 , движущуюся со скоростью конденсата V, так что в ней конденсат покоится. Преобразования Галилея (12) тогда дают
, движущуюся со скоростью конденсата V, так что в ней конденсат покоится. Преобразования Галилея (12) тогда дают
|
|
|
(15) |
Эти результаты очевидны, и мы напомним только, что все это относится к конденсату в основном состоянии. В системе 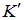 он покоится, а мимо него со скоростью
он покоится, а мимо него со скоростью 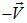 движется трубка. Если есть вязкость, то она проявится в диссипации энергии. Это не может сразу произойти во всей жидкости: сначала возбудятся отдельные внутренние движения, появятся квазичастицы типа фононов. Пусть возникло возбуждение с импульсом
движется трубка. Если есть вязкость, то она проявится в диссипации энергии. Это не может сразу произойти во всей жидкости: сначала возбудятся отдельные внутренние движения, появятся квазичастицы типа фононов. Пусть возникло возбуждение с импульсом 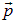 и энергией
и энергией 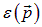 . Для возбужденного конденсата в
. Для возбужденного конденсата в  имеем вполне очевидные соотношения
имеем вполне очевидные соотношения
|
|
|
(16) |
Как эти формулы будут выглядеть в лабораторной системе отсчета? Чтобы перейти назад в K, используем обратные преобразования Галилея:
|
|
|
(17) |
откуда находим
|
|
|
(18) |
Сравнивая формулы (14) и (18), находим изменение энергии движущегося конденсата в лабораторной системе  при переходе из основного состояния в возбужденное:
при переходе из основного состояния в возбужденное:
|
|
|
(19) |
Образование квазичастицы энергетически выгодно, если  . В самом благоприятном для этого случае импульс
. В самом благоприятном для этого случае импульс 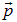 антипараллелен скорости
антипараллелен скорости 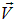 , и изменение энергии конденсата равно
, и изменение энергии конденсата равно
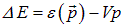 .
.
Отсюда следует, что для торможения жидкости необходимо выполнение условия
|
|
|
(20) |
Здесь мы ввели обозначение  для параметра с размерностью скорости — отношения минимума энергии возбуждения к импульсу. Этот параметр равен угловому коэффициенту штриховой прямой на рис. 3. Если спектр возбуждений таков, что
для параметра с размерностью скорости — отношения минимума энергии возбуждения к импульсу. Этот параметр равен угловому коэффициенту штриховой прямой на рис. 3. Если спектр возбуждений таков, что  , как это и показано, то условие торможения не выполняется при слабых возбуждениях: как говорят, в спектре возбуждения имеется энергетическая щель — некая разность между энергией возбуждения и энергией основного состояния. Это значит, что при малых скоростях
, как это и показано, то условие торможения не выполняется при слабых возбуждениях: как говорят, в спектре возбуждения имеется энергетическая щель — некая разность между энергией возбуждения и энергией основного состояния. Это значит, что при малых скоростях  трение невозможно. Иными словами, мы получили явление сверхтекучести (при малых импульсах скорость
трение невозможно. Иными словами, мы получили явление сверхтекучести (при малых импульсах скорость 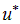 равна скорости звука). Смысл полученного результата в том, что конденсат — это коллективное образование, реагирующее на выпадение одного из своих членов повышением энергии, в то время как трение должно энергию понижать. Закон дисперсии, изображенный на рис. 3, таков, что условие сверхтекучести выполнено. Для обычных бозе-частиц с
равна скорости звука). Смысл полученного результата в том, что конденсат — это коллективное образование, реагирующее на выпадение одного из своих членов повышением энергии, в то время как трение должно энергию понижать. Закон дисперсии, изображенный на рис. 3, таков, что условие сверхтекучести выполнено. Для обычных бозе-частиц с
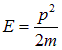
имеем
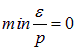 .
.
и условие сверхтекучести не выполнено.
Вывод: обычные частицы даже в конденсатном состоянии сверхтекучестью не обладают, конденсат не образует связанного коллектива и не реагирует на замедление отдельных частиц.
Еще раз подчеркнем: 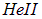 — не смесь различных веществ, и его компоненты невозможно выделить по отдельности. Лучше было бы говорить об одновременном сосуществовании в гелии не компонентов, а двух видов движения — нормального и сверхтекучего.
— не смесь различных веществ, и его компоненты невозможно выделить по отдельности. Лучше было бы говорить об одновременном сосуществовании в гелии не компонентов, а двух видов движения — нормального и сверхтекучего.
Сверхпроводимость. В 1911 г. голландский физик Г. Камерлинг — Оннес открыл удивительное явление. При температуре около 4K электрическое сопротивление ртути скачком уменьшалось до нуля. Впоследствии явление сверхпроводимости было обнаружено им у олова, свинца, таллия и других веществ. Были проведены многочисленные эксперименты по выявлению свойств сверхпроводящего состояния вещества.
Важнейшими свойствами сверхпроводящего состояния вещества являются:
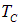 , при которой возникает сверхпроводящее состояние;
, при которой возникает сверхпроводящее состояние;Для большинства известных ранее веществ критические температуры имеют порядок 1–15 K. В 1986 г. были открыты керамические соединения, переходящие в сверхпроводящее состояние при температурах порядка 125 K, то есть выше точки кипения жидкого азота при нормальном давлении. Поскольку ранее сверхпроводники получались лишь при охлаждении материала жидким гелием, а жидкий азот гораздо дешевле в производстве, открытие высокотемпературной сверхпроводимости сулит развитие многочисленных технических приложений.
Критическое значение индукции магнитного поля  , при котором происходит разрушение сверхпроводящего состояния, зависит от температуры сверхпроводника. Характерный график этой зависимости показан на рис. 4; он хорошо описывается формулой
, при котором происходит разрушение сверхпроводящего состояния, зависит от температуры сверхпроводника. Характерный график этой зависимости показан на рис. 4; он хорошо описывается формулой
|
|
|
(21) |
где 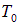 — критическое значение поля при абсолютном нуле температуры.
— критическое значение поля при абсолютном нуле температуры.
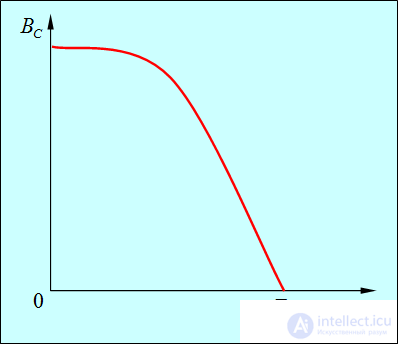
Рис. 4. Значение критического магнитного поля как функция температуры сверхпроводника
Как мы увидим далее в нашем курсе, теплоемкость нормального металла при низких температурах имеет вид
|
|
|
(22) |
где первое слагаемое — уже знакомый нам вклад кристаллической решетки, описываемый теорией Дебая, а второе слагаемое — изучаемый в следующей части курса вклад электронного газа. В сверхпроводнике теплоемкость при очень низких температурах определяется, как показывают эксперименты, выражением типа
|
|
|
(23) |
Первое слагаемое не изменилось: кристаллическая решетка по-прежнему на месте. Драматическое изменение второго слагаемого (экспонента вместо линейной функции) показывает, что сверхпроводимость связана с какими-то коренными изменениями поведения электронов проводимости.
Микроскопическая теория сверхпроводимости была создана Д. Бардиным, Л. Купером и Д. Шрифером и усовершенствована Н.Н. Боголюбовым. Она слишком сложна для изложения в данном учебнике. Достаточно лишь указать на то, что имеется глубокая аналогия между сверхтекучестью и сверхпроводимостью. Из-за взаимодействия электронов с фононами между электронами возникает притяжение, и при определенных условиях может образоваться своеобразное связанное состояние — куперовская пара электронов с противоположными спинами. Такое образование является уже бозоном и может испытывать бозе–эйнштейновскую конденсацию, что и является предпосылкой перехода материала в сверхпроводящее состояние.
При абсолютном нуле температуры электронный газ в сверхпроводнике переходит в основное состояние, обладающее свойствами конденсата. Что очень важно, это состояние отделено энергетической щелью 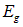 от следующего, возбужденного, состояния. Иначе говоря, чтобы вывести электрон из основного состояния, надо придать ему некоторую минимальную энергию
от следующего, возбужденного, состояния. Иначе говоря, чтобы вывести электрон из основного состояния, надо придать ему некоторую минимальную энергию 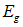 , а меньшие порции энергии просто не будут восприняты. Нечто подобное мы уже видели для сверхтекучего состояния, а еще ранее — для теплоемкости («замораживание» вращательных и колебательных степеней свободы, теория теплоемкости Эйнштейна). Теория предсказывает простую связь энергетической щели и критической температуры:
, а меньшие порции энергии просто не будут восприняты. Нечто подобное мы уже видели для сверхтекучего состояния, а еще ранее — для теплоемкости («замораживание» вращательных и колебательных степеней свободы, теория теплоемкости Эйнштейна). Теория предсказывает простую связь энергетической щели и критической температуры:
 .
.
Наличие энергетической щели сразу объясняет поведение теплоемкости электронного газа. Действительно, энергия 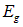 — это минимальная энергия, разрушающая куперовскую пару, и сообщение такой энергии порождает пару свободных электронов. Тогда на каждый электрон приходится половинная энергия
— это минимальная энергия, разрушающая куперовскую пару, и сообщение такой энергии порождает пару свободных электронов. Тогда на каждый электрон приходится половинная энергия 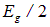 . Из статистических соображений можно утверждать, что число электронов вне основного состояния пропорционально величине
. Из статистических соображений можно утверждать, что число электронов вне основного состояния пропорционально величине
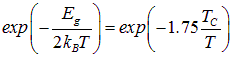 .
.
Тепловая энергия, поглощаемая при возбуждении, пропорциональна
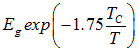 .
.
Производная этой величины по температуре дает теплоемкость электронного газа в сверхпроводящем состоянии:
|
|
|
(24) |
При низких температурах предэкспоненциальный множитель 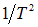 меняется гораздо медленнее экспоненты, так что этот закон практически не отличается от феноменологического соотношения (23). При изменении температуры величина щели изменяется по закону, похожему на изображенный на рис. 4. При критической температуре щель исчезает, и вместе с ней исчезают сверхпроводящие свойства. Заметим, что выражение (24) аналогично формуле для теплоемкости (7.8) в теории Эйнштейна, где также имеется щель между основным и возбужденным уровнями энергии.
меняется гораздо медленнее экспоненты, так что этот закон практически не отличается от феноменологического соотношения (23). При изменении температуры величина щели изменяется по закону, похожему на изображенный на рис. 4. При критической температуре щель исчезает, и вместе с ней исчезают сверхпроводящие свойства. Заметим, что выражение (24) аналогично формуле для теплоемкости (7.8) в теории Эйнштейна, где также имеется щель между основным и возбужденным уровнями энергии.
Из сказанного ясно, какую важную роль играет энергетическая щель. В системе бозонов она ответственна за явления сверхтекучести и сверхпроводимости. В системе фермионов, как мы увидим в дальнейшем, она ответственна за различие свойств металлов, диэлектриков и полупроводников.
Исследования явлений сверхтекучести и сверхпроводимости всегда вызывали большой интерес как ученых, так и общества в целом. «Виной» тому — широкие перспективы их практического использования. Особое значение они приобретают в современном мире, где ученые научились создавать совершенно новые материалы с необычными характеристиками, проявляющие, например, сверхпроводящие свойства при относительно высоких температурах и в достаточно сильных магнитных полях. Не случайно за исследования в этой области присуждена не одна Нобелевская премия, начиная с Камерлинг Оннеса (премия 1913 г.) и заканчивая пока премией 2003 г., которую получили А.А. Абрикосов (Россия и США), В.Л. Гинзбург (Россия) и Э. Леггетт (Великобритания и США).
Исследование, описанное в статье про теплоемкость кристаллов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теплоемкость кристаллов, квантовая статистика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Атомная и Ядерная физика
Часть 1 7. Теплоемкость кристаллов. Квантовая статистика
Часть 2 7.4. Фононы - 7. Теплоемкость кристаллов. Квантовая статистика
Часть 3 7.7. Статистика Бозе — Эйнштейна - 7. Теплоемкость кристаллов. Квантовая
Часть 4 - 7. Теплоемкость кристаллов. Квантовая статистика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика