Лекция
Это продолжение увлекательной статьи про теплоемкость кристаллов.
...
style="text-align:right">(7.41)
Значит, среднее число частиц
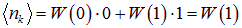
в состоянии k получается равным
|
|
|
(7.42) |
Формула (7.42) является основой квантовой статистики Ферми — Дирака. При высоких температурах получаем
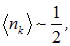
то есть равномерное распределение частиц по состояниям. Если число частиц N в системе фиксировано, то химический потенциал 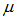 определится из условия
определится из условия
|
|
|
(7.43) |
Подчеркнем также, что согласно (7.42) среднее число частиц в данном состоянии всегда не превышает единицы. Это — прямое следствие принципа Паули.
Рассмотрим теперь систему тождественных бозонов. В этом случае число 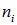 частиц в состоянии i может принимать любое значение от 0 до бесконечности (или от 0 до N при фиксированном числе частиц). Рассмотрим какое-то конкретное состояние k системы с энергией
частиц в состоянии i может принимать любое значение от 0 до бесконечности (или от 0 до N при фиксированном числе частиц). Рассмотрим какое-то конкретное состояние k системы с энергией 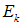 . Тогда для вероятности, что в этом состоянии окажется n частиц, получаем из основного соотношения (7.38)
. Тогда для вероятности, что в этом состоянии окажется n частиц, получаем из основного соотношения (7.38)
|
|
|
(7.44) |
где
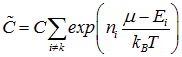 .
.
Сумма W(n) по всем значениям n (включая и нулевое) равна вероятности того, что в состоянии k окажется какое-то количество частиц или не окажется ни одной. Очевидно, такая сумма должна быть равна единице:
|
|
|
(7.45) |
Здесь мы использовали формулу
|
|
|
(7.46) |
для суммы бесконечно убывающей геометрической прогрессии при
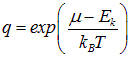 .
.
Теперь легко найти нормировочную постоянную:
|
|
|
(7.47) |
и полное выражение для вероятности W(n). Нас интересует в первую очередь среднее число частиц в состоянии k, которое по смыслу вероятностей выражается как
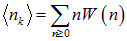 .
.
Сумму ряда вида
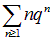
нетрудно вычислить дифференцированием по q выражения (7.46):
|
|
|
(7.48) |
Левая часть (7.48) может быть записана в виде
|
|
|
(7.49) |
Вместе с (7.48) это приводит к результату:
|
|
|
(7.50) |
Подставляя
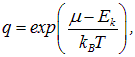
находим
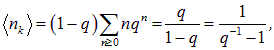
откуда следует основное соотношение квантовой статистики Бозе — Эйнштейна:
|
|
|
(7.51) |
Разница по сравнению с соответствующей формулой (7.42) для фермионов имеется только в знаке перед единицей в знаменателе. Из-за этого нельзя теперь утверждать, что среднее число частиц в данном состоянии всегда меньше единицы: принцип Паули не распространяется на бозоны. По физическому смыслу все 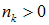 , следовательно,
, следовательно, 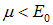 , где
, где 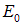 — минимальная энергия системы (то есть энергия основного уровня). Для свободных частиц величина
— минимальная энергия системы (то есть энергия основного уровня). Для свободных частиц величина 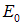 равна нулю. Отсюда следует, что для свободных бозонов химический потенциал отрицателен. По-прежнему имеется уравнение связи
равна нулю. Отсюда следует, что для свободных бозонов химический потенциал отрицателен. По-прежнему имеется уравнение связи 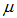 и N в случае фиксированного числа частиц:
и N в случае фиксированного числа частиц:
|
|
|
(7.52) |
При высоких температурах
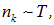
то есть с ростом температуры число бозонов в каждом состоянии растет.
Если в системе число частиц не фиксировано, а определяется условиями равновесия (например, равновесие излучения с веществом, когда фотоны поглощаются и испускаются), то 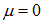 . Применяя (7.51) к системе фотонов и учитывая, что для фотонов
. Применяя (7.51) к системе фотонов и учитывая, что для фотонов
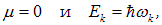
приходим к формуле (7.15) и ее аналогу для фононов (7.30).
Заметим, что при
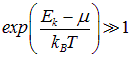
обе формулы (7.42) и (7.51) переходят в классическое распределение Больцмана. В этом случае
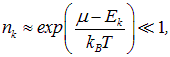
что можно интерпретировать как условие малой плотности частиц, то есть как квантовый аналог разреженного газа: в каждом квантовом состоянии фактически находится не более одной частицы. Значит, не существенно не только прямое взаимодействие частиц, но и их квантовое влияние друг на друга, так называемые обменные эффекты.
Не следует думать, будто законы квантовой механики важны только при рассмотрении явлений в масштабах атомов и молекул. При низких температурах вблизи абсолютного нуля существуют и макроскопические проявления этих законов. С ними мы и познакомимся в этом разделе.
Бозе-эйнштейновская конденсация. Рассмотрим идеальный газ свободных бозонов, которые не взаимодействуют ни друг с другом, ни с внешним полем. Состояние частицы задается ее импульсом р и проекцией спина (имеется всего g = 2s + 1 возможностей, для бозонов s — целое число). Среднее число бозонов в данном состоянии к описывается формулой (7.51). Поскольку принцип запрета Паули на бозоны не распространяется, они могут накапливаться в одном состоянии. При нулевой температуре все частицы системы должны занять нижний энергетический уровень с Е = 0. Возникает вопрос, что будет при 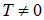 ?
?
Снова вспомним формулу (7.14) для числа типов колебаний, но заменим в ней волновой вектор на импульс частицы:
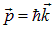 .
.
Получаем тогда
|
|
|
(1) |
Индексом «сост» мы хотим подчеркнуть, что, имея дело с квантовыми частицами, мы стали называть вещи своими именами: число колебаний становится в этом случае числом состояний, в которых можно обнаружить частицу. Элемент объема пространства импульсов можно записать в виде
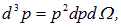
где 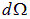 — телесный угол. Интегрируя соотношение (1) по углам, получаем число состояний
— телесный угол. Интегрируя соотношение (1) по углам, получаем число состояний 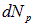 , в которых модуль импульса частицы заключен между значениями р и р + dp:
, в которых модуль импульса частицы заключен между значениями р и р + dp:
|
|
|
(2) |
Учитывая, что энергия свободной нерелятивистской частицы
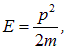
так что
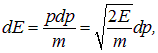
находим из (1) число состояний 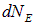 с энергиями между E и E + dE:
с энергиями между E и E + dE:
|
|
|
(3) |
Умножая (3) на среднее число частиц в одном состоянии, находим число частиц, приходящееся на тот же интервал энергий:
|
|
|
(4) |
Чтобы получить полное число частиц в системе, проинтегрируем (4) по всем значениям энергии:
|
|
|
(5) |
Вводя новую переменную интегрирования
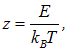
переписываем (5) в виде
|
|
|
(6) |
Это уравнение для вычисления химического потенциала 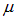 . В сущности, мы переписали формулу (7.52) в виде, удобном для практического применения: суммирование по всем возможным состояниям заменено на суммирование (интеграл) по энергии частицы, а число состояний учтено у нас при использовании формулы (3).
. В сущности, мы переписали формулу (7.52) в виде, удобном для практического применения: суммирование по всем возможным состояниям заменено на суммирование (интеграл) по энергии частицы, а число состояний учтено у нас при использовании формулы (3).
Если при заданной концентрации частиц N/V понижать температуру газа, то химический потенциал будет увеличиваться (то есть уменьшаться по модулю), как следует из (6). Предельного значения 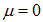 он достигнет при температуре
он достигнет при температуре 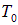 , определяемой уравнением
, определяемой уравнением
|
|
|
(7) |
откуда следует выражение для 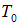 :
:
|
|
|
(8) |
Разберемся в физическом смысле входящих в формулу (8) комбинаций параметров. Если обозначить через l среднее расстояние между частицами, то в объеме сферы радиусом l/2 будет содержаться одна частица, то есть плотность частиц будет
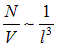 .
.
Поэтому формулу (8) можно переписать в виде
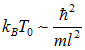 .
.
Поскольку тепловая энергия движения частиц
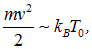
мы получаем отсюда
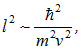
или
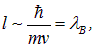
где 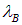 — длина волны де Бройля (мы опустили в этом рассуждении несущественные числовые множители). Таким образом, снова приходим к выводу, что квантовые эффекты становятся заметными, когда длина волны де Бройля имеет порядок расстояния между частицами. Формула (8) — это общее выражение для «квантовой» температуры: оно еще нам встретится, а меняться может лишь числовой множитель.
— длина волны де Бройля (мы опустили в этом рассуждении несущественные числовые множители). Таким образом, снова приходим к выводу, что квантовые эффекты становятся заметными, когда длина волны де Бройля имеет порядок расстояния между частицами. Формула (8) — это общее выражение для «квантовой» температуры: оно еще нам встретится, а меняться может лишь числовой множитель.
Итак, при 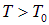 существует физически приемлемое (
существует физически приемлемое (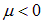 ) решение уравнения (6). При
) решение уравнения (6). При 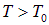 химический потенциал остается равным предельному значению 0, дальше ему меняться некуда, и правая часть уравнения становится меньше N/V. Этот результат удивителен, ибо число частиц в системе фиксировано, и плотность частиц, казалось бы, должна оставаться неизменной. Стало быть, какая-то доля этих частиц куда-то девается, выпадает из системы, перестает участвовать в тепловом движении. Значит, правая часть (6) будет при
химический потенциал остается равным предельному значению 0, дальше ему меняться некуда, и правая часть уравнения становится меньше N/V. Этот результат удивителен, ибо число частиц в системе фиксировано, и плотность частиц, казалось бы, должна оставаться неизменной. Стало быть, какая-то доля этих частиц куда-то девается, выпадает из системы, перестает участвовать в тепловом движении. Значит, правая часть (6) будет при 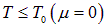 описывать те частицы, которые в тепловом движении участвуют, то есть энергия которых больше нуля:
описывать те частицы, которые в тепловом движении участвуют, то есть энергия которых больше нуля:
|
|
|
(9) |
Если умножить и разделить правую часть (9) на
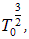
то можно выделить фактор
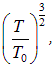
а оставшийся сомножитель, в соответствии с (7), будет равен полному числу N частиц в системе:
|
|
|
(10) |
Остальные частицы имеют нулевую энергию; их число 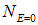 определится как разность
определится как разность 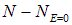 :
:
|
|
|
(11) |
Итак, при температуре ниже критической 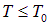 происходит так называемая бозе-эйнштейновская конденсация — накопление частиц в состоянии с
происходит так называемая бозе-эйнштейновская конденсация — накопление частиц в состоянии с 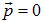 . Эффект этот — макроскопический, так как число частиц конденсата огромно, порядка полного числа частиц N. При понижении температуры ниже критической конденсат появляется внезапно — система испытывает резкое изменение свойств (как говорят, происходит фазовый переход).
. Эффект этот — макроскопический, так как число частиц конденсата огромно, порядка полного числа частиц N. При понижении температуры ниже критической конденсат появляется внезапно — система испытывает резкое изменение свойств (как говорят, происходит фазовый переход).
При абсолютном нуле температуры все частицы системы находятся в конденсате. При повышении температуры некоторые из них покидают конденсат и начинают участвовать в тепловом движении. При 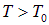 бозе-эйнштейновский конденсат исчезает: в нем не остается частиц. Зависимость доли частиц в конденсате от температуры показана на рис. 1.
бозе-эйнштейновский конденсат исчезает: в нем не остается частиц. Зависимость доли частиц в конденсате от температуры показана на рис. 1.
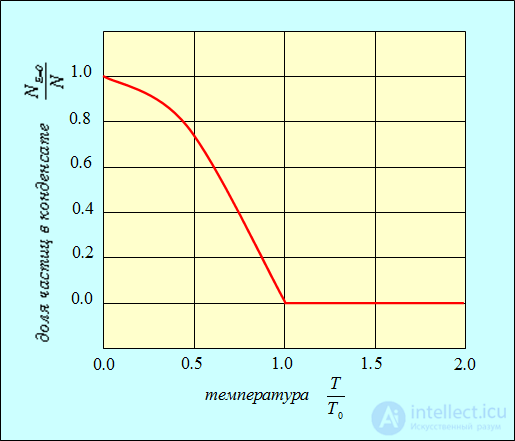
Рис. 1. Доля частиц в бозе-эйнштейновском конденсате в зависимости от температуры
Важно отметить, что конденсация происходит не в обычном пространстве, как при выпадении, например, росы, но в пространстве импульсов. С точки зрения нашего обычного пространства и конденсат, и нормальный компонент бозе-газа «размешаны», и система остается пространственно однородной. Но есть и сходство с обычным насыщенным паром: например, при 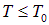 давление не зависит от объема системы, что для идеального газа необычно.
давление не зависит от объема системы, что для идеального газа необычно.
Явление, предсказанное Эйнштейном и индийским физиком Бозе много лет назад, впервые экспериментально наблюдалось в 1995 г. в США. «Газ» из 2 000 атомов рубидия, охлажденный почти до абсолютного нуля (20 нK), «сконденсировался» в «суператом», который вел себя уже не как газ частиц, но как единое целое. Таким образом, было создано новое состояние вещества, никогда ранее не существовавшее в естественном виде во Вселенной, как было сказано в сообщении об этих работах. В 2001 г. авторам этих экспериментальных работ была присуждена Нобелевская премия.
Явление сверхтекучести. Сверхтекучесть — это свойство жидкого гелия протекать без трения сквозь тонкие капилляры при низких температурах  . Явление открыто П.Л. Капицей в 1938 г. (Нобелевская премия была присуждена в 1978 г.). Дальнейшие исследования показали, что в жидком гелии как бы имеются два компонента: нормальный и сверхтекучий. Из-за отсутствия вязкости сверхтекучий гелий не оказывает сопротивления погруженным телам. В сверхтекучем состоянии жидкий гелий проявляет так много необычных свойств, что мы вправе считать сверхтекучий компонент особым состоянием вещества, которое принято обозначать
. Явление открыто П.Л. Капицей в 1938 г. (Нобелевская премия была присуждена в 1978 г.). Дальнейшие исследования показали, что в жидком гелии как бы имеются два компонента: нормальный и сверхтекучий. Из-за отсутствия вязкости сверхтекучий гелий не оказывает сопротивления погруженным телам. В сверхтекучем состоянии жидкий гелий проявляет так много необычных свойств, что мы вправе считать сверхтекучий компонент особым состоянием вещества, которое принято обозначать  (в отличие от обычного
(в отличие от обычного  ). Упомянем лишь так называемый эффект фонтанирования: при освещении карманным фонарем нижнего конца капилляра, опущенного в жидкий гелий, он нагревается и доля сверхтекучего компонента падает. Избыточное давление заставляет втекать в капилляр сверхтекучий компонент, что приводит к появлению фонтанчика высотой до 30–40 см. Такое перетекание гелия от холодного места к горячему необычно: в нормальных жидкостях все происходит как раз наоборот.
). Упомянем лишь так называемый эффект фонтанирования: при освещении карманным фонарем нижнего конца капилляра, опущенного в жидкий гелий, он нагревается и доля сверхтекучего компонента падает. Избыточное давление заставляет втекать в капилляр сверхтекучий компонент, что приводит к появлению фонтанчика высотой до 30–40 см. Такое перетекание гелия от холодного места к горячему необычно: в нормальных жидкостях все происходит как раз наоборот.
Фазовая диаграмма для гелия представлена на рис. 2.
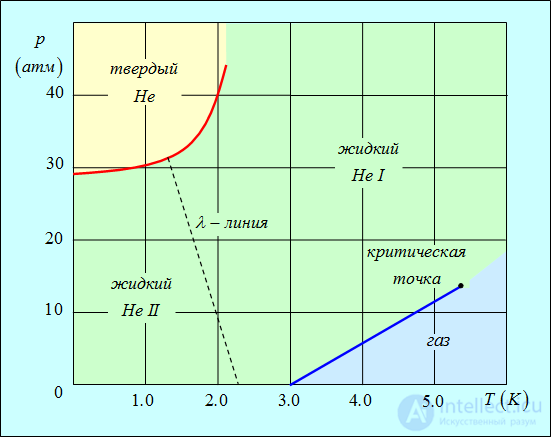
Рис. 2. Фазовая диаграмма для 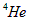 (по осям отложены давление и температура).
(по осям отложены давление и температура).
Штрихами показана 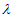 —линия между нормальным (Не I) и сверхтекучим (Не II) состояниями
—линия между нормальным (Не I) и сверхтекучим (Не II) состояниями
Фазовый переход 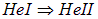 происходит на так называемой
происходит на так называемой 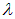 -линии, причем температура перехода уменьшается с ростом давления. Сверхтекучее состояние наблюдалось для изотопа
-линии, причем температура перехода уменьшается с ростом давления. Сверхтекучее состояние наблюдалось для изотопа 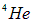 (сверхтекучесть у другого изотопа
(сверхтекучесть у другого изотопа 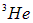 увидели гораздо позже и с большим трудом, но это — другая история). Поскольку протон и нейтрон, входящие в ядро гелия, имеют спин 1/2, то спин ядра
увидели гораздо позже и с большим трудом, но это — другая история). Поскольку протон и нейтрон, входящие в ядро гелия, имеют спин 1/2, то спин ядра 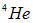 — целый, а
— целый, а 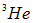 — полуцелый. Здесь возникает разница между бозонами и фермионами. Частицы жидкого
— полуцелый. Здесь возникает разница между бозонами и фермионами. Частицы жидкого 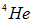 — бозоны, и они могут претерпевать конденсацию Бозе-Эйнштейна. К тому же при типичной концентрации частиц в жидкости
— бозоны, и они могут претерпевать конденсацию Бозе-Эйнштейна. К тому же при типичной концентрации частиц в жидкости 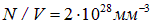 , массе ядра гелия
, массе ядра гелия 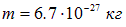 и g = 1 (полный спин ядра равен нулю) формула (8) дает для температуры бозе-эйнштейновской конденсации значение
и g = 1 (полный спин ядра равен нулю) формула (8) дает для температуры бозе-эйнштейновской конденсации значение 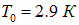 , что не так далеко от температуры
, что не так далеко от температуры 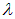 -перехода. Представляется весьма соблазнительным связать два необычных состояния вещества — бозе-эйнштейновский конденсат и сверхтекучий компонент. Но все не так просто, как кажется.
-перехода. Представляется весьма соблазнительным связать два необычных состояния вещества — бозе-эйнштейновский конденсат и сверхтекучий компонент. Но все не так просто, как кажется.
Элементы микроскопической теории сверхтекучести. Дело в том, что жидкость — не идеальный газ, там имеется сильное взаимодействие между частицами. А мы рассматривали конденсат в системе идеального газа бозонов. И надо еще разобраться, почему конденсат должен проявлять сверхтекучесть. Согласно микроскопической теории Н.Н. Боголюбова (1947), нельзя говорить о состоянии отдельных атомов гелия, но лишь о состоянии всей системы. Здесь мы впервые встречаемся с квантовой жидкостью — макроскопическим квантовым эффектом. При T = 0 система находится в основном состоянии, при повышении температуры возникают тепловые возбуждения, переход на низколежащие возбужденные уровни энергии. Коллективные возбуждения атомов квантуются аналогично колебаниям атомов кристаллической решетки в теории Дебая. Там при квантовании возникали фононы, здесь — квазичастицы, отдельные кванты с
продолжение следует...
Часть 1 7. Теплоемкость кристаллов. Квантовая статистика
Часть 2 7.4. Фононы - 7. Теплоемкость кристаллов. Квантовая статистика
Часть 3 7.7. Статистика Бозе — Эйнштейна - 7. Теплоемкость кристаллов. Квантовая
Часть 4 - 7. Теплоемкость кристаллов. Квантовая статистика
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика