Лекция
Привет, Вы узнаете о том , что такое колебательное движение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое колебательное движение, колебание, параметрический резонанс, вынужденные колебания , настоятельно рекомендую прочитать все из категории Колебания и волны (Оптика, акустика и радиофизика).
|
Колебания — это физические процессы, характеризующиеся той или иной степенью повторяемости. |
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д.
В зависимости от характера воздействия на колеблющееся тело различают свободные (или собственные) и вынужденные колебания.
Если положение системы в любое время может быть описано единственным параметром, то система имеет одну степень свободы. Примеры таких систем: маятник, колеблющийся в заданной плоскости; масса, связанная с пружиной; LC-цепочка (рис. 1.1). Обычно для таких систем употребляют общее название осциллятор (от англ. oscillate — колебаться, вибрировать).

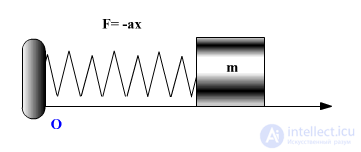

Рис. 1.1. Примеры колебательных систем с одной степенью свободы.
В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.
Пружинный маятник
|
Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной |
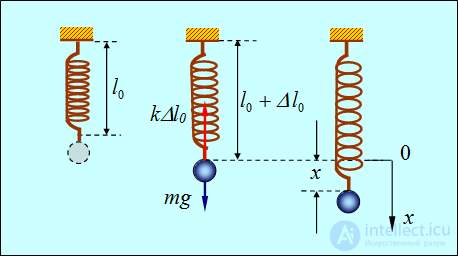
Рис. 1.2. К выводу уравнения движения для пружинного маятника
В положении равновесия (рис. 1.2) сила тяжести  уравновешивается упругой силой
уравновешивается упругой силой 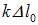 :
:

откуда
|
|
|
(1.1) |
где  – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.
– статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.
Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным  . По закону Гука проекция результирующей силы на ось ОХ будет тогда равна
. По закону Гука проекция результирующей силы на ось ОХ будет тогда равна
|
|
|
(1.2) |
Учитывая, что
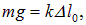
получим
|
|
|
(1.3) |
Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.
Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:
|
|
|
(1.4) |
|
|
|
|
Видео 1.1 Грузы на пружинах. Зависимость частоты колебаний от массы груза и жесткости пружины
Математический маятник
|
Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. |
Будем характеризовать отклонение маятника от положения равновесия углом  , который образует нить с вертикалью (рис. 1.3).
, который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника
При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести 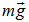 и сила натяжения нити
и сила натяжения нити  . Соответственно, уравнение движения этой материальной точки имеет вид
. Соответственно, уравнение движения этой материальной точки имеет вид
 .
.
Проецируя его на направления нормали и касательной к траектории (окружности радиуса  ), получаем
), получаем

Модуль скорости  равен
равен  , учитывая, что при движении точки к положению равновесия угол
, учитывая, что при движении точки к положению равновесия угол  убывает, а скорость точки
убывает, а скорость точки  растет, напишем
растет, напишем
 .
.
Тогда второе из написанных выше уравнений движения приобретает вид
|
|
|
(1.5) |
При малых отклонениях маятника от вертикали, когда  ,
,

получаем:
|
|
|
(1.6) |
Физический маятник
|
Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку. |
Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника
При отклонении маятника от положения равновесия на угол  возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен
возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен
|
|
|
(1.7) |
где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс Cмаятника.

Рассматривая  как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков
как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков  и
и  можно объяснить тем, что векторы
можно объяснить тем, что векторы  и
и 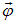 направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:
направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:
|
|
|
(1.8) |
Ограничимся рассмотрением малых отклонений от положения равновесия:
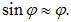
В этом случае уравнение колебаний принимает вид:
|
|
|
(1.9) |
В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.
Колебания поршня в сосуде с идеальным газом
Рассмотрим цилиндр с площадью поперечного сечения 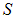 , в который вставлен поршень массы
, в который вставлен поршень массы 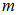 (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты
(рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты  , над поршнем воздух с постоянным (атмосферным) давлением
, над поршнем воздух с постоянным (атмосферным) давлением  . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен
. Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен  и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.
и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом
В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления  и давления
и давления 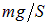 , оказываемого поршнем. Обозначим это результирующее давление
, оказываемого поршнем. Обозначим это результирующее давление 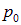 :
:
|
|
|
(1.10) |
Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона
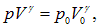
откуда
|
|
|
(1.11) |
Здесь 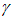 — показатель адиабаты, зависящий от числа степеней свободы молекул газа.
— показатель адиабаты, зависящий от числа степеней свободы молекул газа.
При малых колебаниях, когда изменение объема газа  много меньше его «равновесной» величины
много меньше его «равновесной» величины  , то есть когда
, то есть когда

выражение (1.11) можно разложить в ряд Тейлора:
|
|
|
(1.12) |
На поршень действуют три силы: сила атмосферного давления  , сила давления газа под поршнем
, сила давления газа под поршнем 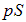 и сила тяжести
и сила тяжести  . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей
. Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей  этих сил:
этих сил:
|
|
|
(1.13) |
Используя (1.13), уравнение движения поршня

можно записать в следующем виде
|
|
|
(1.14) |
Электромагнитный контур
Рассмотрим колебательный контур, состоящий из конденсатора емкостью C и катушки индуктивностью L (рис. 1.6).

Рис. 1.6. Электромагнитный колебательный контур: 1 – t = 0; 2 – t = Т/4; 3 – t = Т/2; 4 – t = 3Т/4; 5 – t = Т
Сопротивлением катушки и проводов пренебрегаем. Пусть в цепи идет ток I, заряжающий конденсатор:

Так как внешняя ЭДС к контуру не приложена, то ЭДС самоиндукции
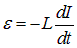
равна напряжению q/C на конденсаторе.
Имеем два уравнения:
|
|
|
(1.15) |
Подставляя первое уравнение во второе, получаем уравнение для изменения заряда на конденсаторе:
|
|
|
(1.16) |
Вместо использованной подстановки выражения тока через заряд можно продифференцировать второе из уравнений (1.15) и выразить производную от заряда через ток. В результате получим аналогичное уравнение для изменения тока в цепи:
|
|
|
(1.17) |
с тем же выражением для  , что и в (1.16).
, что и в (1.16).
Мы рассмотрели несколько физически совершенно различных систем, и убедились, что уравнения движения приводятся к одной и той же форме
|
|
|
(1.18) |
Различия между физическими системами проявляются лишь в различном определении величины  и в различном физическом смысле переменной x: это может быть координата, угол, заряд, ток и т. д. Отметим, что при этом, как следует из самой структуры уравнения (1.18), величина
и в различном физическом смысле переменной x: это может быть координата, угол, заряд, ток и т. д. Отметим, что при этом, как следует из самой структуры уравнения (1.18), величина  всегда имеет размерность обратного времени.
всегда имеет размерность обратного времени.
Уравнение (1.18) описывает так называемые гармонические колебания.
|
Гармонические колебания — это такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса. |
Уравнение гармонических колебаний (1.18) является линейным дифференциальным уравнением второго порядка (так как оно содержит вторую производную от переменной x). Линейность уравнения означает, что
Доказана также математическая теорема, согласно которой уравнение второго порядка имеет два независимых решения. Все остальные решения, согласно свойствам линейности, могут быть получены как их линейные комбинации. Непосредственным дифференцированием легко проверить, что независимые функции 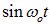 и
и  удовлетворяют уравнению (1.18). Значит, общее решение этого уравнения имеет вид:
удовлетворяют уравнению (1.18). Значит, общее решение этого уравнения имеет вид:
|
|
|
(1.19) |
где C1, C2 — произвольные постоянные. Это решение может быть представлено и в другом виде. Введем величину
|
|
|
(1.20) |
и определим угол 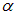 соотношениями:
соотношениями:
|
|
|
(1.21) |
Тогда общее решение (1.19) записывается как
|
|
|
(1.22) |
Согласно формулам тригонометрии, выражение в скобках равно
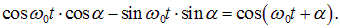
Окончательно приходим к общему решению уравнения гармонических колебаний в виде:
|
|
|
(1.23) |
Неотрицательная величина A называется амплитудой колебания, 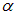 — начальной фазой колебания. Весь аргумент косинуса — комбинация
— начальной фазой колебания. Весь аргумент косинуса — комбинация  — называется фазой колебания.
— называется фазой колебания.
Выражения (1.19) и (1.23) совершенно эквивалентны, так что мы можем пользоваться любым их них, исходя из соображений простоты. Оба решения являются периодическими функциями времени. Действительно, синус и косинус периодичны с периодом  . Поэтому различные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени t*, за который фаза колебания получает приращение, кратное
. Поэтому различные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени t*, за который фаза колебания получает приращение, кратное  :
:
|
|
|
(1.24) |
Отсюда следует, что

Наименьшее из этих времен
|
|
|
(1.25) |
называется периодом колебаний (рис. 1.8), а 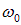 — его круговой (циклической) частотой.
— его круговой (циклической) частотой.
Рис. 1.8.
Используют также и частоту колебаний
|
|
|
(1.26) |
|
Частота колебаний |
Соответственно, круговая частота равна числу колебаний за  секунд.
секунд.
|
В системе СИ единицей измерения частоты являются обратные секунды, для которых введено специальное название — герц (1 Гц=1/c). |
Итак, если система в момент времени t характеризуется значением переменной x(t), то, то же самое значение, переменная  будет иметь через промежуток времени
будет иметь через промежуток времени 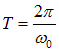 (рис.1.9), то есть
(рис.1.9), то есть

Это же значение, естественно, повторится через время 2T, ЗT и т. д.

Рис. 1.9. Период колебаний
В общее решение входят две произвольные постоянные (C1, C2 или A, a), значения которых должны определяться двумя начальными условиями. Обычно (хотя и не обязательно) их роль играют начальные значения переменной x(0) и ее производной 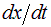 .
.
Приведем пример. Пусть решение (1.19) уравнения гармонических колебаний описывает движение пружинного маятника. Значения произвольных постоянных зависят от способа, каким мы вывели маятник из состояния равновесия. Например, мы оттянули пружину на расстояние  и отпустили шарик без начальной скорости. В этом случае
и отпустили шарик без начальной скорости. В этом случае

Подставляя t = 0 в (1.19), находим значение постоянной С2
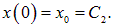
Решение, таким образом, имеет вид:

Скорость груза находим дифференцированием по времени

Подставляя сюда t = 0, находим постоянную С1:

откуда

Окончательно

Сравнивая с (1.23), находим, что  — это амплитуда колебаний, а его начальная фаза равна нулю:
— это амплитуда колебаний, а его начальная фаза равна нулю:  .
.
Выведем теперь маятник из равновесия другим способом. Об этом говорит сайт https://intellect.icu . Ударим по грузу, так что он приобретет начальную скорость  , но практически не сместится за время удара. Имеем тогда другие начальные условия:
, но практически не сместится за время удара. Имеем тогда другие начальные условия:
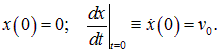
Так как

наше решение имеет вид

Скорость груза будет изменяться по закону:
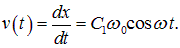
Подставим сюда 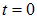 :
:

откуда

Окончательно получаем:

так что амплитуда колебаний равна

а начальная фаза

В общем случае, когда начальное смещение маятника из положения равновесия  , а начальная скорость
, а начальная скорость  , связь этих величин с амплитудой и начальной фазой колебания имеет вид
, связь этих величин с амплитудой и начальной фазой колебания имеет вид
|
|
|
(1.27) |
Дифференцируя решение (1.22) по времени, найдем зависимость от времени скорости и ускорения маятника:

Соответствующие графики представлены на рис. 1.10 (для простоты мы положили начальную фазу  ). Видно, что скорость и ускорение также изменяются по гармоническому закону, причем амплитуда скорости равна
). Видно, что скорость и ускорение также изменяются по гармоническому закону, причем амплитуда скорости равна  , а амплитуда ускорения
, а амплитуда ускорения  . Скорость опережает смещение по фазе на
. Скорость опережает смещение по фазе на  , ускорение находится в противофазе по отношению к смещению. Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот.
, ускорение находится в противофазе по отношению к смещению. Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот.

Рис. 1.10. Зависимость от времени положения, скорости и ускорения колеблющейся материальной точки
Умножим уравнение (1.18) гармонических колебаний на скорость изменения переменной x:
|
|
|
(1.28) |
Каждое из слагаемых можно представить как соответствующую производную:


так что уравнение (1.28) записывается в виде:
|
|
|
(1.29) |
Отсюда следует, что величина в скобках не зависит от времени, то есть сохраняется в процессе колебаний:
|
|
|
(1.30) |
Для выяснения физического смысла сохраняющейся величины применим эти соотношения к пружинному маятнику, когда
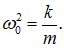
Видим, что уравнение (1.30) можно записать в виде суммы кинетической энергии груза и потенциальной энергии деформированной (сжатой или растянутой) пружины:
|
|
|
(1.31) |
Таким образом, найденный закон сохранения есть не что иное, как закон сохранения полной энергии системы.
Аналогично, для электромагнитного контура переменная
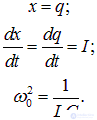
и

В этом случае соотношение (1.30) принимает вид:
|
|
|
(1.32) |
Первый член — это энергия магнитного поля в катушке, а второй — энергия электрического поля в конденсаторе. Снова мы получили, что сохраняется полная энергия системы.
Возвращаясь к общей форме (1.30) закона сохранения энергии и подставляя сюда общее решение (1.23), получаем законы изменения во времени кинетической и потенциальной энергий (или их аналогов) и выражение для сохраняющейся полной энергии:
|
|
|
(1.33) |
Отсюда следует, что
Видео 1.9 Сохранение энергии при почти гармонических колебаниях – маятник Галилея.
Сказанное проиллюстрировано на рис. 1.11, на котором показаны изменения кинетической и потенциальной энергий для пружинного маятника и электромагнитного контура.

Рис. 1.11. Изменения во времени различных форм энергии в колебательной системе:
1 – пружинный маятник; 2 – электромагнитный колебательный контур
Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.
Сложение колебаний с одинаковыми частотами
Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:
|
|
|
(1.34) |
где x1, x2 — переменные, описывающие колебания, A1, A2 — их амплитуды, а  ,
,  — начальные фазы. Результирующее
колебание
— начальные фазы. Результирующее
колебание

удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.
Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол  . Если привести этот вектор во вращение с угловой скоростью
. Если привести этот вектор во вращение с угловой скоростью  , то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону
, то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону
|
|
|
(1.35) |
Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).

Рис. 1.12. Векторная диаграмма для общего решения (1.23)
Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А1 и А2 Возьмем их векторную сумму (рис. 1.13)


Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты
Проекция вектора А1 на ось 0x равна сумме проекций соответствующих векторов

Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью 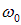 , так что результирующее движение будет гармоническим колебанием с частотой
, так что результирующее движение будет гармоническим колебанием с частотой  , амплитудой A и начальной фазой a. Согласно теореме косинусов:
, амплитудой A и начальной фазой a. Согласно теореме косинусов:
|
|
|
(1.36) |
В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную  (то есть
(то есть 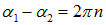 ), то амплитуда результирующего колебания равна сумме амплитуд
), то амплитуда результирующего колебания равна сумме амплитуд

Если же складываемые колебания находятся в противофазе (то есть 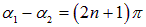 ), то
), то
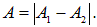
Биения
В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые биениями.
|
Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами. |
Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно,  и
и 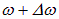 . Итак,
. Итак,
|
|
|
(1.37) |
Складываем эти выражения и учитываем известную формулу тригонометрии:
|
|
|
(1.38) |
Если  то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:
то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:
|
|
|
(1.39) |
Кроме того, множитель в скобках меняется медленно по сравнению с 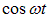 . Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой w, эффективная амплитуда
. Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой w, эффективная амплитуда  которого изменяется со временем по закону (1.40) (рис. 1.14):
которого изменяется со временем по закону (1.40) (рис. 1.14):
|
|
|
(1.40) |
Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону 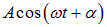 , причем все три его параметра:
, причем все три его параметра:  строго постоянны во времени.
строго постоянны во времени.

Рис. 1.14. Биения при сложении колебаний с близкими частотами
Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен
|
|
|
(1.41) |
Видео 1.12 Биения на экране осциллографа
Видео 1.13 Биения: осциллограф и динамик
Видео 1.14 «Двойной» маятник: запись песком картины биений
Колебания двух связанных осцилляторов
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).

Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается
Тогда в положении равновесия координаты грузов равны

При колебаниях координаты равны, соответственно, x1(t), x2(t). Удлинения пружин записываются как

Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная

и сила со стороны пружины K, равная

На второй груз действуют аналогичные силы

и

Соответственно, уравнения движения имеют вид
|
|
|
(1.42) |
Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x1 оказывают влияния колебания x2 и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными колебаниями (модами)). Именно, введем новые переменные x1 и x2:
|
|
|
(1.43) |
Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат
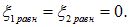
В этих переменных уравнения (1.42) принимают вид:
|
|
|
(1.44) |
Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:
|
|
|
(1.45) |
Первое уравнение описывает гармонические колебания с частотой
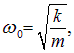
совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой

Так как K<, имеем
|
|
|
(1.46) |
Соответственно, мы получаем общее решение системы уравнений:
|
|
|
(1.47) |
Общее решение для координат х1 и х2 колеблющихся точек следуют из (1.47) и (1.43):
|
|
|
(1.48) |
Для примера рассмотрим случай, когда первая масса смещается на расстояние  от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:
от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:
|
|
|
(1.49) |
Этому соответствуют следующие начальные значения нормальных координат:
|
|
|
(1.50) |
Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид
|
|
|
(1.51) |
Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:
|
|
|
(1.52) |
Графики функций x1(t), x2(t) показаны на рис. 1.16. Видна характерная картина биений.

Рис. 1.16. Биения в системе двух связанных осцилляторов
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время  первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту
первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту  первый маятник колеблется с максимальной амплитудой, а второй покоится.
первый маятник колеблется с максимальной амплитудой, а второй покоится.
На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.

Рис. 1.17. Биения в системе связанных маятников
Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x1), то A2 = 0 и, как следует из общего решения (1.48),
|
|
|
(1.53) |
Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов
Возбуждение только второй (x2) нормальной моды означает, что A1 = 0:
|
|
|
(1.54) |
В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.
В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.
В этом разделе мы рассмотрим сложение двух гармонических колебаний одинаковой частоты  , происходящих во взаимно перпендикулярных направлениях вдоль осей x и y. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю:
, происходящих во взаимно перпендикулярных направлениях вдоль осей x и y. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю:
|
|
|
(1.55) |
где  — разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию
— разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию 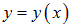 .
.
Рассмотрим сначала частные случаи. Пусть разность фаз равна нулю: 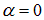 . Тогда
. Тогда
|
|
|
(1.56) |
то есть траектория точки представляет собой прямую. Аналогичная траектория получится при колебаниях с разностью фаз 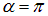
|
|
|
(1.57) |
При разности фаз  находим:
находим:
|
|
|
(1.58) |
Из (1.58) и (1.55) следует уравнение эллипса:
|
|
|
(1.59) |
причем точка движется по часовой стрелке (для стандартного направления осей: ось ОХ — направо, ось ОУ — вверх). При разности фаз  находим:
находим:
|
|
|
(1.60) |
Это приводит к той же эллиптической траектории (1.59), только вращение в этом случае происходит против часовой стрелки.
Если амплитуды колебаний по осям х и у одинаковы ( ), то из (1.59) получается круговая траектория.
), то из (1.59) получается круговая траектория.
В общем случае произвольной разности фаз  траектория также будет представлять собой эллипс, но с повернутыми осями (рис. 1.18).
траектория также будет представлять собой эллипс, но с повернутыми осями (рис. 1.18).

Рис. 1.18. Траектории материальной точки, колеблющейся с одинаковыми частотами
в перпендикулярных направлениях, при различных разностях фаз:
1 — 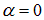 или
или  (штриховая линия); 3 —
(штриховая линия); 3 —  ; 2 —
; 2 — 
Видео 1.15 Маятник Айри: запись песком фигур Лиссажу
Видео 1.16 Фигуры Лиссажу на экране осциллографа
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет довольно сложный вид. Замкнутые траектории, описываемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, возникают тогда, когда отношение частот складываемых колебаний есть рациональное число, называются такие траектории фигурами Лиссажу.
Одна из простейших фигур Лиссажу получается при отношении частот 2:1 и нулевых начальных фазах  :
:

откуда
|
|
|
(1.61) |
Мы получили уравнение параболы.
Форма фигур Лиссажу зависит от соотношения частот складываемых колебаний и разности фаз между ними. Примеры сложения колебаний с различными соотношениями частот показаны на рис. 1.19 и 1.20.
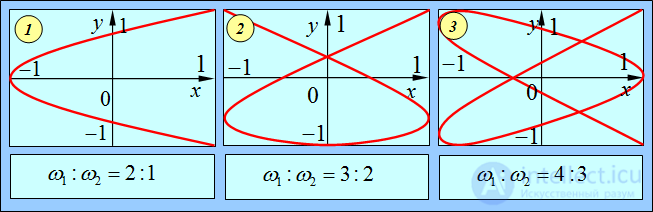
Рис. 1.19. Примеры фигур Лиссажу для указанных отношений частот и нулевых значений начальных фаз каждого колебания.
Координата x выражена в единицах амплитуды колебаний A, координата y – в единицах амплитуды B.
Частота  относится к колебаниям вдоль оси x,
относится к колебаниям вдоль оси x,  – вдоль оси y
– вдоль оси y
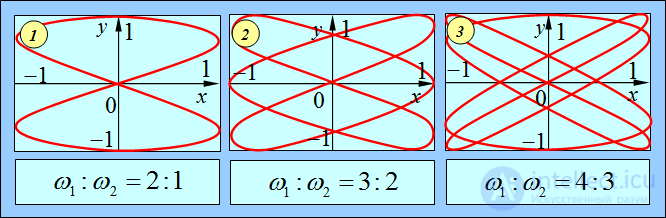
Рис. 1.20. Примеры фигур Лиссажу для тех же отношений частот, что на рис. 1.19 и одинаковых же начальных фазах каждого колебания 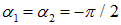 , то есть при
, то есть при 

Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.
Уравнение затухающих колебаний
Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости
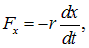
где r — соответствующий коэффициент, зависящий от вязкости среды, размеров и формы тела. Поэтому уравнение движения примет вид:
|
|
|
(1.62) |
или
|
|
|
(1.63) |
Здесь 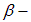 новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если
новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если 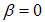 .
.
Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:
|
|
|
(1.64) |
Подставляем первое уравнение во второе:
|
|
|
(1.65) |
или
|
|
|
(1.66) |
Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.
Анализ решений
Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:
|
|
|
(1.67) |
|
|
|
|
 — коэффициент затухания, a
— коэффициент затухания, a 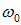 — циклическая частота свободных (собственных) незатухающих колебаний (то есть при
— циклическая частота свободных (собственных) незатухающих колебаний (то есть при  , при отсутствии потерь энергии). Сведем новую задачу к предыдущей. Для этого вместо переменной x определим новую переменную X, связанную с x соотношением:
, при отсутствии потерь энергии). Сведем новую задачу к предыдущей. Для этого вместо переменной x определим новую переменную X, связанную с x соотношением:|
|
|
(1.68) |
Дифференцируя функцию x(t), получаем:
|
|
|
(1.69) |
Подставляем эти выражения в (1.67):
|
|
|
(1.70) |
Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной 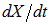 . Получаем в итоге дифференциальное уравнение для функции X(t):
. Получаем в итоге дифференциальное уравнение для функции X(t):
|
|
|
(1.71) |
Здесь возможны два случая. Пусть сначала  . Тогда можно ввести параметр
. Тогда можно ввести параметр
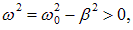
так что уравнение (1.71) примет вид:
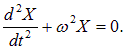
Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:

Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):
|
|
|
(1.72) |
Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний:  . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой
. Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой  и с амплитудой, изменяющейся по закону (рис. 1.22)
и с амплитудой, изменяющейся по закону (рис. 1.22)


Рис. 1.22. Свободные затухающие колебания
Видео 1.17 Механические (маятник) затухающие колебания — запись песком
Видео 1.18 Затухание колебаний камертона — осциллограф и собственные уши
Коэффициент затухания 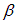 определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
Период затухающих колебаний равен:
|
|
|
(1.73) |
Пусть первое наибольшее положительное отклонение достигается в момент времени  . Последующие наибольшие отклонения того же знака (A', A'', A''' и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:
. Последующие наибольшие отклонения того же знака (A', A'', A''' и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:
|
|
|
(1.74) |
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:
|
|
|
(1.75) |
Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:
|
|
|
(1.76) |
Определим количество колебаний, которое совершит система за время  . За это время амплитуда уменьшается в е раз, а число колебаний равно:
. За это время амплитуда уменьшается в е раз, а число колебаний равно:
|
|
|
(1.77) |
Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется величина, называемая добротностью:
|
|
|
(1.78) |
которая пропорциональна числу колебаний Nе, совершаемых системой за то время  , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при
, за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при 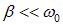 находим:
находим:
|
|
|
(1.79) |
Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (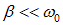 ) имеем:
) имеем:
|
|
|
(1.80) |
где E0 — значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:
|
|
|
(1.81) |
Следовательно,
|
|
|
(1.82) |
то есть при слабом затухании добротность, с точностью до множителя  , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
, равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.
При увеличении затухания частота колебаний
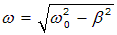
стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при 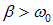 движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
В случае вынужденных колебаний система колеблется под действием периодической внешней (вынуждающей) силы. За счет работы этой силы компенсируются потери энергии системы. Частота вынужденных колебаний зависит от частоты изменения внешней силы (для краткости мы будем называть ее "вынуждающей частотой"). Практически наиболее интересным является случай, когда вынуждающая сила изменяется по гармоническому закону:

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом.
|
Резонанс — это явление резкого увеличения амплитуды вынужденных колебаний при определенной частоте внешнего воздействия, называемой резонансной частотой системы. |
Видео 1.21 Резонансное взаимодействие маятников
Видео 1.22 Камертоны: резонансное поглощение энергии волны
Видео 1.23 Резонанс доски с мотором
Явление резонанса используется для усиления колебаний, например электрических. Однако при конструировании машин и сооружений необходимо учитывать явление резонанса, чтобы предотвратить чаще всего нежелательные, а иногда и разрушительные последствия резонансного увеличения амплитуды вынужденных колебаний.
Для пружинного маятника уравнение вынужденного колебательного движения имеет вид:
|
|
|
(1.83) |
или
|
|
|
(1.84) |
где

и  — вынуждающая частота.
— вынуждающая частота.
Если рассматривать электрический колебательный контур, то компенсировать потери энергии в контуре можно с помощью подводимой извне периодически изменяющейся по гармоническому закону ЭДС или переменного напряжения
|
|
|
(1.85) |

Рис. 1.25. Вынужденные колебания в электромагнитном контуре
Уравнение колебаний в контуре (рис. 1.25) можно записать, используя закон Ома для замкнутой цепи
|
|
|
(1.86) |
или, с учетом, что 
|
|
|
(1.87) |
где

— собственная частота контура,
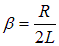
— коэффициент затухания, a

Таким образом, вынужденные колебания в электрическом контуре описываются тем же самым линейным неоднородным дифференциальным уравнением второго порядка, что и в случае колебаний пружинного маятника. Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение  . Тогда разность любого другого решения q(t) и этого частного решения
. Тогда разность любого другого решения q(t) и этого частного решения 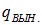 будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как
будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как
|
|
|
(1.88) |
где

— частота свободных затухающих колебаний.
С течением времени из-за экспоненциального множителя 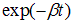 роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при
роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при
 ,
,
им можно пренебречь, сохраняя лишь первое слагаемое. Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).
Частное решение неоднородного уравнения будем искать в виде гармонической функции, частота изменения которой совпадает с частотой вынуждающей силы:
|
|
|
(1.89) |
Подставим  в виде (1.89) в уравнение (1.87):
в виде (1.89) в уравнение (1.87):
|
|
|
(1.90) |
Так как функции синуса и косинуса линейно независимы, коэффициенты при них в левой части (1.90) должны быть равны нулю:
|
|
|
(1.91) |
Решение этой системы имеет вид:
|
|
|
(1.92) |
Решение (1.89) с коэффициентами (1.92) можно записать в стандартном виде:
|
|
|
(1.93) |
где
|
|
|
(1.94) |
и
|
|
|
(1.95) |
При знаке минус в фазе косинуса в выражении (1.93) начальная фаза 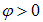 имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).
имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).
Видео 1.24 Резонансный язычковый частотомер
Видео 1.25 Спектр модулированного колебания
Рассмотрим отклик системы на изменение частоты внешней силы. Под квадратным корнем в выражении для амплитуды стоит квадратичная функция частоты

Эта функция имеет минимум (а значит, амплитуда имеет максимум).
Для нахождения точки минимума дифференцируем функцию  по
по  и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты
и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты
|
|
|
(1.96) |
и амплитуды установившихся вынужденных колебаний при резонансе
|
|
|
(1.97) |
Следует отметить, что при  значение резонансной частоты
значение резонансной частоты  практически совпадает с собственной частотой
практически совпадает с собственной частотой  колебательной системы. Поскольку
колебательной системы. Поскольку  стоит в знаменателе выражения для
стоит в знаменателе выражения для  , резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.
, резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.

Рис. 1.26. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы
При увеличении частоты внешнего воздействия амплитуда стремится к нулю:

Физически это понятно: система обладает некой инерционностью и не успевает следовать за быстрыми изменениями внешнего воздействия. В другом предельном случае малой внешней частоты

мы имеем дело со статическим случаем — действием постоянной внешней силы F0 на пружинный маятник, или подсоединением контура к источнику с постоянным напряжением Um. В этом случае предельное значение амплитуды вынужденных колебаний равно

и не зависит от затухания. Последнее вполне естественно, так как затухание обусловлено действием силы сопротивления, которая пропорциональна скорости и проявляется только при движении системы, а не в статическом пределе. В случае механических колебаний
|
|
|
(1.98) |
что равно удлинению пружины под действием постоянной силы F0.
В случае электромагнитных колебаний в контуре
|
|
|
(1.99) |
что равно заряду на конденсаторе при подсоединении его к источнику постоянного напряжения Um.
Найдем отношение резонансной амплитуды к статической при малом затухании, когда 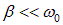 :
:
|
|
|
(1.100) |
Иными словами, добротность Q характеризует также резонансные свойства колебательной системы: чем больше добротность, тем выше и относительно уже резонансный пик (см. рис. 1.26).
Автоколебательные системы. параметрический резонанс .

Исследование, описанное в статье про колебательное движение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое колебательное движение, колебание, параметрический резонанс, вынужденные колебания и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Колебания и волны (Оптика, акустика и радиофизика)
Комментарии
Оставить комментарий
Базовая физика
Термины: Базовая физика