2.8. Классификация электромагнитных явлений и полей -Статическое , Стационарное, Квазистатическое , нестационарное кратко

Привет, Вы узнаете о том , что такое электромагнитные явления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое электромагнитные явления, статическое поле, стационарное эмп, квазистатическое поле, нестационарное поле , быстропеременное поле , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

Классификация электромагнитных явлений в теории электромагнитного поля строится на основе различных проявлений взаимодействия электрических и магнитных полей, их источников и свойств.

На основании зависимости характеристик поля от времени вводится классификация электромагнитных явлений.
1. статическое поле 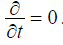. Поля неизменные во времени

.
Система уравнений Максвелла разбивается на две независимые системы, одна из которых описывает поля неподвижных зарядов (электростатика):
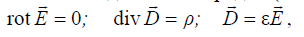, (2.20)
а вторая – поля постоянных магнитов (магнитостатика):
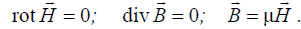. (2.21)
2. стационарное эмп – это поле, создаваемое постоянными токами:

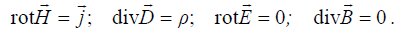. (2.22)
3. квазистатическое поле создается медленно меняющимися токами, когда можно считать, что
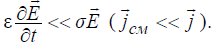. (2.23)
4. Нестационарное (быстропеременное) поле – описывается всей системой уравнений Максвелла.

электромагнитные явления охватывают широкий спектр физических процессов, начиная от статических полей до высокоэнергетических электромагнитных волн. Эти явления объединены уравнениями Максвелла, которые служат фундаментальной основой теории электромагнитного поля. Классификация позволяет упрощать их изучение и понимать закономерности взаимодействий.

В отличие от электростатического поля стационарное электрическое поле существует не только в диэлектрике, но и в проводнике при наличии постоянного тока проводимости. Уравнения стационарного электрического поля похожи на уравнения электростатического поля (σ =const):

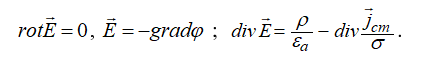(12.16)

Потенциал стационарного поля определяется уравнением Пуассона (11.11).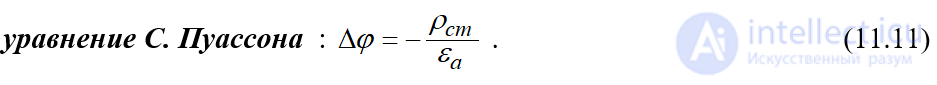

Объемная плотность заряда выражается формулой:

. (12.17)

Из (12.16) следует, что объемные электрические заряды могут существовать только в тех областях проводящей среды, где отсутствуют сторонние токи.

На границе раздела двух проводящих сред линии тока преломляются в соответствии с граничным условием (4.3) :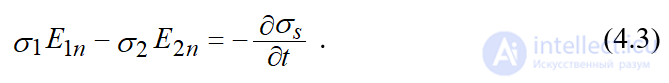

. (12.18)

Если проводимости сред различаются сильно (σ2>>σ1), то в слабо проводящей среде 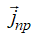проходит практически по нормали, независимо от расположения вектора плотности тока в среде с большей проводимостью. Об этом говорит сайт https://intellect.icu . В таком случае поверхность металлических тел, находящихся в диэлектрике, можно считать эквипотенциальной (σ=const).

В некоторых случаях для стационарного электрического поля в области свободной от сторонних зарядов и токов применим метод электростатической аналогии, который позволяет свести задачу стационарного электрического поля к задачам электростатики. В этом случае граничные условия для составляющих вектора плотности тока аналогичны граничным условиям для вектора электрической индукции. Переход к уравнениям электростатики для систем с одинаковыми геометрическими размерами осуществляется с помощью следующей замены переменных :

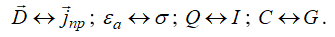(12.19)

Метод электростатической аналогии используется при анализе ЭМП линий передачи с Т-волной (коаксиальная линия и т. п.). С другой стороны электростатическая аналогия позволяет экспериментально исследовать сложные электростатические поля с помощью их моделирования в ванне со слабо проводящей жидкостью (электролитом) .

Уравнения стационарного магнитного полязаписываются в виде:

. (12.20)

В (12.20) уже заметна связь между электрическим и магнитным полями.

Наиболее распространенной задачей является определение стационарного магнитного поля по заданному распределению токов. Для изотропной линейной однородной среды анализ ЭМП удобно проводить с помощью .

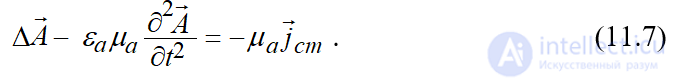
Для векторного потенциала стационарного магнитого поля условие калибровки (11.6) и волновое уравнение (11.7) записываются в виде:

, . (12.21)

Решение (12.21) относительно A(r) соответствует решению волнового уравнения Гельмгольца при k=0 :

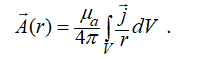. (12.22)

В простых случаях при наличии симметрии поля более удобным может оказаться прямой расчет 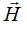по (3.4).

Например, магнитное поле круглого провода с током и коаксиальной линии в силу цилиндрической симметрии удобно находить именно по (3.4).

Контур интегрирования удобно совмещать с векторными линиями .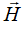

Для круглого провода радиусаа с электрическим током I:

. (12.23)

График распределения магнитного поля в проводнике H(r)приведен на рис. 12.3.

Для коаксиальной линии передачи (рис. 12.2) :

. (12.24)

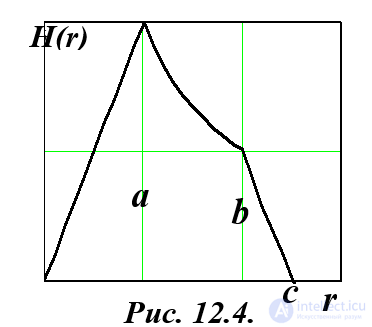
График распределения магнитного поля в коаксиальной линии приведен на рис. 12.4.

Вывод данных формул, а также другие примеры стационарных магнитных полей можно найти в [Фальковский О. И. Техническая электродинамика: Учебник для вузов связи.- М.: Связь, 1978.- 432 с.].

Энергия стационарного магнитного поля:

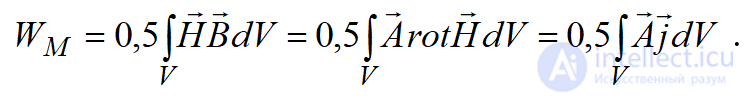. (12.25)

Сравнивая с (12.6) можно заметить определенное сходство уравнений стационарного магнитного поля с уравнениями электростатики.

Полную энергию стационарного магнитного поля системы из n контуров с токами удобно выражать через токи и индуктивности (см. пояснение к (9.18)):

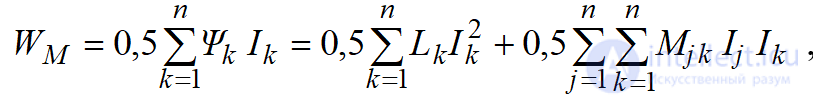, (12.26)

где 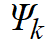– потокосцеплениеk-го контура, – собственная индуктивность k-го контура, 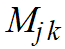– взаимная индуктивность j-го и k-го контуров .

Первое слагаемое (12.26) представляет сумму собственных энергий магнитных полей контуров, а второе слагаемое (12.26) – взаимную энергию магнитных полей создаваемых токами в данных контурах.

С помощью анализа запаса магнитной энергии в системе можно вычислять индуктивность проводников и линий передачи Т-волны.

Магнитный поток, проходящий через поперечное сечение линии передачи удобно разложить на внутренний и внешний. Внутренний поток, проходящий внутри проводников, связан с собственными индуктивностями проводников.

Внешний магнитный поток определяется линиями 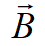во внешней по отношению к проводникам среде и связан с взаимной индуктивностью.

Например, погонная индуктивность коаксиальной линии передачи (рис. 12.2) при постоянном токе определяется формулой ( μ 1 – μ диэлектрика, а μ 2 – μ проводников) :

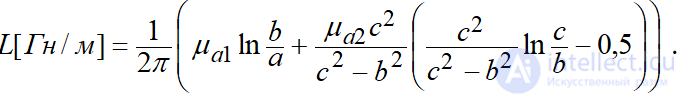. (12.27)

Первое слагаемое (12.27) соответствует взаимной индуктивности проводников, а второе – собственной индуктивности. Обычно в справочниках приводится формула (12.28), соответствующая току высокой частоты:

. (12.28)

следует помнить о том, что в данной формуле a– это абсолютная магнитная проницаемостьдиэлектрика.

Аналогичным образом вычисляется индуктивность двухпроводной линии передачи (рис. 12.1) (1 –  диэлектрика, а 2 –  проводников) :

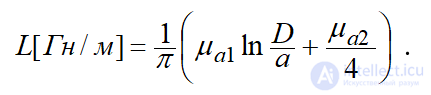. (12.29)

Первое слагаемое (12.29) соответствует взаимной индуктивности проводников, а второе – собственной индуктивности двух цилиндрических проводников. Обычно в справочниках приводится формула (12.30), соответствующая переменному току высокой частоты [4, 5, 11] :

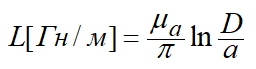. (12.30)

При анализе многосвязных линий передачи Т-волны (количество проводников в данных линиях больше двух) и соединений с их использованием составляют матрицы взаимных емкостей и индуктивностей проводников линии на основании (12.6) и (12.26).

Квазистационарным ЭМП в области V называют ЭМП, для которого можно пренебречь волновым характером. Для квазистационарного поля время, в течение которого источники поля успевают заметно измениться, велико по сравнению со временем запаздывания волнового фронта (l/v). (l – расстояние в области V, которое со скоростью v проходит распространяющаяся ЭМВ.)

Время запаздывания – это время, необходимое для распространения ЭМ возмущения от одного конца системы до другого .

Для квазистационарного ЭМП справедливы следующие соотношения:

, . (12.31)

В случае монохроматических колебаний плоская волна превращается в колебание во времени : 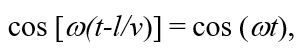, откуда следует еще одно условие квазистационарности поля: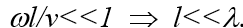

Таким образом, при монохроматических процессах ЭМ системы можно исследовать с помощью законов квазистационарного ЭМП в тех случаях, когда их протяженность много меньше длины волны .

Быстропеременное ЭМП описывается системой уравнений Максвелла без каких-либо упрощений, характеризуется глубокой взаимосвязью между электрическими и магнитными явлениями и имеет волновой характер.

Исследование, описанное в статье про электромагнитные явления, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое электромагнитные явления, статическое поле, стационарное эмп, квазистатическое поле, нестационарное поле , быстропеременное поле и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля

Из статьи мы узнали кратко, но содержательно про электромагнитные явления