Лекция
Привет, Вы узнаете о том , что такое метод конечных элементов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод конечных элементов , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.
метод конечных элементов относится к так называемым прямым методам, суть которых состоит в сведении задачи решения дифференциального или интегрального уравнения относительно неизвестной функции к задаче решения конечной системы алгебраических уравнений. Рассмотрим этот метод на примере решения задачи нахождения скалярного электрического потенциала в следующей постановке.
Пусть в заданной замкнутой области V, ограниченной поверхностью S, распределен заряд с известной объемной плотностью (r ) r ρ . Необходимо найти функцию (r ) r ϕ , описывающую распределение скалярного электрического потенциала в замкнутом объеме и удовлетворяющую уравнению Пуассона следующего вида:
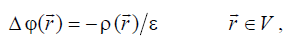 (6.40)
(6.40)
для которого задано обобщенное граничное условие Неймана:
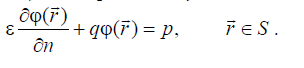 (6.41)
(6.41)
В теории и практике прямых методов для решения таких задач часто используется вариационный подход, позволяющий заменить исходную задачу интегрирования дифференциального уравнения другой задачей, ей равносильной, состоящей в отыскании минимума некоторого функционала. При таком подходе процесс отыскания решения можно условно разбить на два этапа, первый из которых состоит в построении функционала, эквивалентного исходному дифференциальному уравнению, а второй – в преобразовании этого функционала в систему линейных алгебраических уравнений и ее численном решении.
Воспользуемся этим подходом для решения поставленной задачи и на первом его этапе образуем в функционал относительно неизвестной функции (r ) r ϕ , взяв за основу уравнение Пуассона (6.40) вместе с граничным условием (6.41). Для этого поступим следующим образом. Умножим левую и правую
части уравнения (6.40) на некоторую функцию v(r ) r , которая непрерывн вместе со своими двумя производными в V и удовлетворяет граничным усло виям (6.41). Затем проинтегрируем левую и правую части полученного равенства по объему V:

Для дальнейшего преобразования выражения (6.42) воспользуемся 1-й формулой Грина (Б.27):

,
в которую сделаем следующие подстановки: v(r ) r Ψ = и Φ = ϕ, что в результате дает:

а затем заменяя здесь первое слагаемое, используя равенство (6.42):
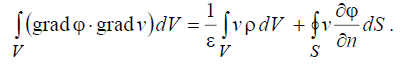 . (6.43)
. (6.43)
Теперь, используя граничное условие (6.41), найдем нормальную производную искомой функции:

и подставим ее в последнее выражение, которое приобретает окончательный вид:
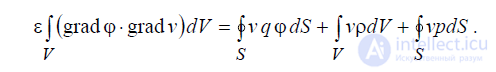 . (6.44)
. (6.44)
Левая часть полученного равенства представляет собой функционал от
неизвестной функции (r ) r ϕ , а правая его часть выражена через известные функции и величины. Таким образом, мы построили нужный нам функционал путем тождественных преобразований исходного уравнения (6.40) и заданных граничных условий (6.41), что дает право считать выполненным первый этап решения поставленной задачи.
Приступим теперь ко второму этапу решения задачи, цель которого состоит в преобразовании выражения (6.44) в систему линейных алгебраических уравнений по методу Бубнова-Галеркина. Для этого выберем бесконечную последовательность линейно независимых базисных функций n (r ) r ψ , которые дважды дифференцируемы в замкнутой области V и удовлетворяю граничным условиям нашей задачи. Если искомую функцию (r ) r ϕ представить в виде разложения
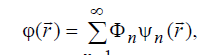 (6.45)
(6.45)
где Φn – произвольно выбранные постоянные, то она также будет удовлетворять граничным условиям задачи, поскольку уравнение (6.40) и граничные условия (6.41) линейные.
При реальных вычислениях разложение (6.45) должно быть конечным, нотогда новая функция
 (6.46)
(6.46)
будет несколько отличаться от (r ) r ϕ . Однако, при выполнении требования
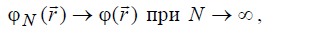 (6.47)
(6.47)
можно всегда найти такое N, при котором это отличие не будет превышать
допустимое.
По методу Бубнова-Галеркина коэффициенты Φn определяются из требования, чтобы выполнялось равенство (6.44) при подстановке в него N (r )
r ϕ
вместо (r ) r ϕ и n (r )
r ψ (n = 1,K,N ) вместо v(r ) r . Выполнив эти операции, приходим к равенству:
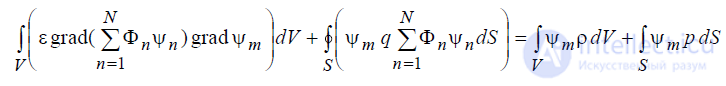
Теперь, поменяв местами операции интегрирования и суммирования,
имеем:
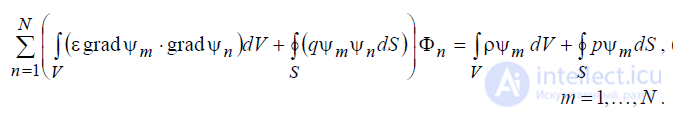 (6.48)
(6.48)
Полученное выражение представляет собой систему уравнений N–го порядка с N неизвестными Φn . Данную систему линейных уравнений можно
записать в матричной форме:
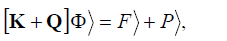 , (6.49)
, (6.49)
где K и Q – квадратные матрицы, Φ , F и P – матрицы столбцы, элементы
которых определяются следующими соотношениями:
 (6.50)
(6.50)
Решение системы (6.50) имеет вид:
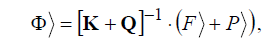 (6.51)
(6.51)
где −1 – операция обращения матрицы.
Таким образом, мы нашли коэффициенты разложения в ряд (6.46) неизвестной функции N (r ) r ϕ , которая при достаточно больших N близка к искомой функции (r ) r ϕ , то есть нашли приближенное решение поставленной задачи. Вместе с тем, это решение нами получено пока формально, поскольку окончательно не выбраны базисные функции n (r )
r ψ , хотя требования мы предъявили к ним достаточно жесткие. Теперь переходим непосредственно к выбору этих функций, что, в конечном итоге, и определяет название метода
конечных элементов.
Для упрощения изложения сделаем выбор базисных функций на примере двумерной задачи, т.е. когда искомое электрическое поле зависит только от
двух координат (например, x и y) и уравнение (6.40) при ε = const в прямоугольной системе координат приобретает вид:
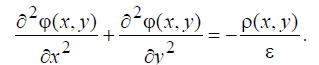 . (6.52)
. (6.52)
Областью определения функции (r) r ϕ теперь является площадь Ω на плоскости xOy (а не объем V, как в случае трехмерной задачи), а ее границей – контур ∂Ω (вместо поверхности S). Поэтому граничные условия (6.41) здесь
приобретают вид:
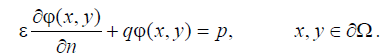
Построим систему базисных функций ψN следующим образом. Разобьем
область Ω на элементы в виде треугольников, в результате чего она покроется сеткой с треугольными ячейками (рис.6.5,а). Пусть полное количество узлов сетки равно М, N из которых них лежит внутри области Ω, а остальные L
расположены на ее границе ∂Ω (M = N + L ).

Теперь определим свойства функций ψn ( n = 1KM ). Пусть каждая базисная функция ψn – это кусочно-линейная функция, принимающая значение ψn =1 в узле с номером n и тождественно равная нулю во всей области
Ω, за исключением нескольких треугольников, имеющих общую вершину в
n-м узле. В пределах примыкающих к n-м узлу треугольников, функция изменяется по линейному закону, падая от единицы в их общей вершине (n-музле) до нуля на границе образованного ими многоугольника (на рис.6.5,а
заштрихован). Графическим изображением функции ψn является поверхность, имеющая форму пирамиды с вершиной в n–м узле (рис.6.5,б) и основанием в виде упомянутого заштрихованного многоугольника. Поскольку
каждый треугольник имеет три вершины, он будет входить в три многоугольника, следовательно внутри его ненулевыми могут быть всего три базисные функции ψk , ψm и ψn , индексы которых k, m, n совпадают с номерами узлов, которые являются вершинами данного треугольника. Таким образом, искомая функция может быть записана в виде суммы:
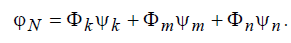 . (6.53)
. (6.53)
Из свойств базисных функций и равенства (6.53) следует, что в n–м узле
значение искомой функции (rn ) r ϕ определяется равенством ϕ(rn ) = Φn r . Следовательно, коэффициенты Φn ( n = 1KM ), определяемые из решения системы линейных уравнений (6.51), есть значения искомой функции в узлах
построенной сетки. Функция (r ) r ϕ в пределах каждого элемента является линейной. К примеру, в декартовой системе координат она может быть описана
функцией вида:
ϕ(x, y) = ax + by + c ,
где a, b и c – коэффициенты, однозначно определяемые координатами узлов
и коэффициентами Φn .
Таким образом, решение уравнения (6.24) найдено. Геометрической интерпретацией решения есть поверхность, составленная из отдельных треугольников. Открытым остается лишь вопрос: на какое число элементов не-
обходимо разбить область Ω, чтобы решение было приемлемо для пользователя? Аналогичную задачу решает архитектор, которому необходимо выложить сферический купол собора треугольной черепицей. Если размер черепицы выбрать большим, то работу можно выполнить быстро и с небольшими затратами, однако купол будет ребристым и мало напоминать сферу. Если черепицу выбрать очень маленьких размеров, то купол будет выглядеть гладким и красивым, однако трудоемкость его изготовления будет высока. Поэтому необходимо искать оптимальный размер плоского элемента поверхности (черепицы), который, с одной стороны, позволял с достаточной точностью создать сферическую поверхность, а с другой стороны, не привел бы к чрезмерным затратам времени и средств. Так и в методе конечных элементов, чтобы повысить точность решения, надо уменьшать площадь элементарных ячеек, что естественно увеличивает вычислительные затраты. И в этом случае надо искать компромисс между приемлемой точностью решения и допустимыми затратами вычислительных ресурсов. Поэтому в рамках данного метода разработана специальная стратегия по выбору оптимального количества ячеек и их размеров. Она предполагает неравномерное разбиение всей исследуемой области Ω, когда элементы на разных участках поверхности отличаются друг от друга по размеру. Там, где ожидается резкое изменение искомая функция, ячейки выбирают меньших размеров, чем там, где функция изменяется достаточно плавно. Такая стратегия позволяет добиться примерно одинаковой точности воспроизведения искомой функции во всей области ее определения, избежав при этом избыточных вычислений.
Метод конечных элементов положен в основу программы моделирования электромагнитных полей, реализованных в приложении PDE Toolbox популярной и мощной системы компьютерной математика MATLAB. Он оказался очень эффективным при решении и многих других прикладных задач, и не только в электродинамике. Сейчас метод конечных элементов интенсивно развивается и круг области его применения непрерывно расширяется.
Исследование, описанное в статье про метод конечных элементов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое метод конечных элементов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля
Комментарии
Оставить комментарий
Теория электромагнитного поля
Термины: Теория электромагнитного поля