2.2. Закон взаимодействия точечных зарядов и его обобщение кратко

Привет, Вы узнаете о том , что такое 2.2. Закон взаимодействия точечных зарядов и его обобщение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2.2. Закон взаимодействия точечных зарядов и его обобщение , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

Одним из фундаментальных опытных законов, лежащих в основе современной ЭД, является закон взаимодействия между точечными зарядами (закон Кулона), который можно записать в виде:

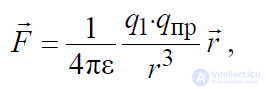
где q1 – основной заряд, который создает электрическое поле, qпр – пробный
заряд.
Напряженность и индукция электрического поля, создаваемого точечным
зарядом q1, могут быть найдены следующим образом:

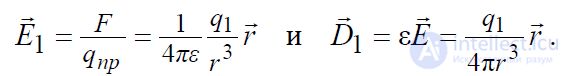
Обобщим закон Кулона на случай N точечных зарядов, сосредоточенных в некотором объеме V (рис.2.2).

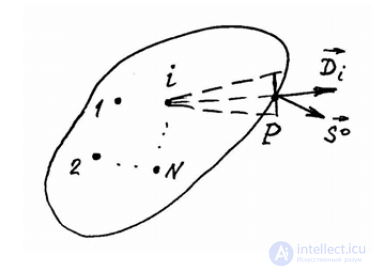
Рис.2.2

Согласно принципу суперпозиции, вектор индукции D
r
результирующего поля будет
равен геометрической сумме векторов индукции
i D
r полей отдельных зарядов:

.
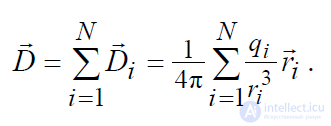
Найдем поток результирующего вектора D
r
через поверхность S, ограничивающую рассматриваемую область

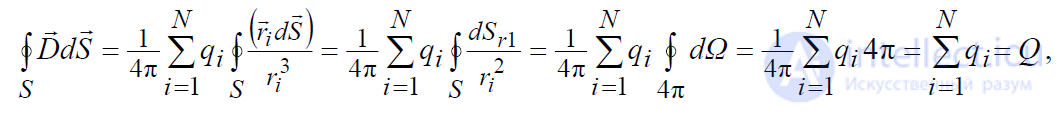
где 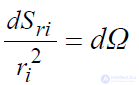- элемент телесного угла.

В результате выполненных операций, можно получить закон Гаусса для индукции электрического поля:
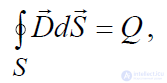(2.4)
который формулируется следующим образом:
Поток вектора индукции электрического поля через замкнутую поверх-
ность S равен суммарному заряду, сосредоточенному в объеме V, ограничен-
ному этой поверхностью.
Найдем дифференциальный аналог закона Гаусса для зарядов, непрерыв-
но распределенных в объеме V с заданной объемной плотностью ρ(x,y,z).

Остроградского-Гаусса:
,
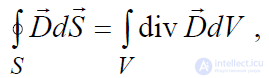а заряд в правой части выразим через его объемную плотность:
.
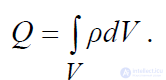Подставляя эти величины в равенство (2.4) приходим к следующему выражению:
,
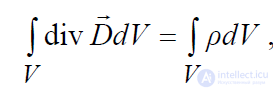откуда следует искомое выражение:
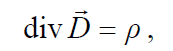(2.5)
которое иногда называют законом Гаусса в дифферен-
циальной форме.
Обе формы закона Гаусса свидетельствуют о том,
что источниками электрического поля D
r
являются элек-
трические заряды Q. Об этом говорит сайт https://intellect.icu . Если внутри рассматриваемой области V имеются электрические заряды, то поток вектора
D r
выходит из V через S. Графически это можно изобразить так: силовые линии поля D
r
начинаются внутри
объема V, а если Q<0, то поток извне входит внутрь V ,
где силовые линии и заканчиваются. Т. о. силовые линии электрического поля (рис.2.3), создаваемого электрическими зарядами, начинается и заканчивается на зарядах (или уходят в
∞ ). Электрические поля такой структуры называются потенциальными.

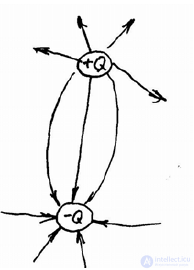
Рисунок 2.3

Исследование, описанное в статье про 2.2. Закон взаимодействия точечных зарядов и его обобщение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 2.2. Закон взаимодействия точечных зарядов и его обобщение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля