10 Энергия электростатического поля

Привет, Вы узнаете о том , что такое энергия электростатического поля, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энергия электростатического поля , настоятельно рекомендую прочитать все из категории Теория электромагнитного поля.

1. Энергия дискретной системы и непрерывно распределенных в пространстве зарядов

Рассмотрим систему п проводников, на которых распределено (по поверхности) п зарядов qi (рис. 1).

Энергия, запасенная в электростатическом поле в объеме V, равна

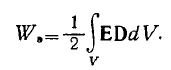
Рис. 1
V
Подставляя под интеграло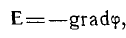м имеем

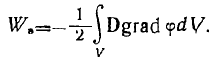
Учитывая равенство

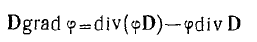
— и имея в виду, что вне проводников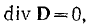

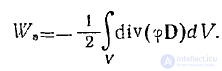
Воспользовавшись теоремой Остроградского—Гаусса и тем, что потенциал каждого проводника постоянен, найдем

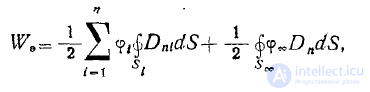
где S„—поверхность сферы очень большого радиуса, включающей все проводники.
В последней формуле считаем нормали к поверхностям проводников внешними по отношению к проводникам. Вспомним, что в теореме Остроградского—Гаусса нормали должны быть внешними по отношению к той области, в которой теорема применяется.

Интеграл по поверхности сферы 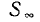должен стремиться к нулю с увеличением радиуса сферы 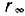, поскольку

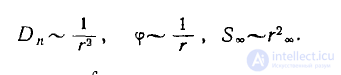
Учитывая далее, что 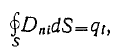окончательно находим

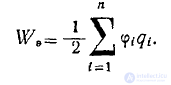(1),

Выражение (1), используя так называемые коэффициенты электростатической индукции 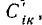определяемые формулой

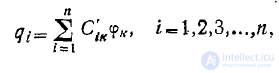
можно представить в виде

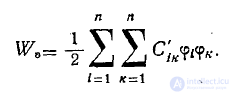
Эти коэффициенты, как следует из равенства

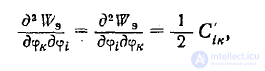
симметричны, т. е.

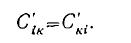
Заметим, что коэффициенты электростатической индукции отличаются от так называемых коэффициентов взаимной емкости
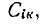, поскольку последние определяются формулой

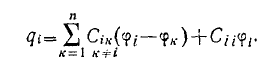
Коэффициенты взаимной емкости являются обобщением понятия обычной емкости конденсатора

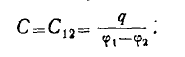
Между коэффициентами взаимной емкости и коэффициентами электростатической индукции, как нетрудно установить из приведенных формул, имеется связь:

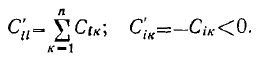
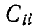— называется собственной емкостью;
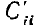— коэффициенты емкости.

Ясно, что формула (1) применима и к случаю системы точечных зарядов. Об этом говорит сайт https://intellect.icu . В этом случае <р,- — это потенциал в точке, где находится заряд qi и созданный всеми остальными зарядами.

В частности, для энергии взаимодействия двух зарядов

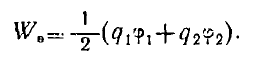. (2)

Здесь может возникнуть вопрос: откуда взялся множитель 1/2 ?
Согласно элементарным соображениям энергия взаимодействия двух зарядов qt и q2 равна 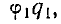, т. е. работе,, совершаемой против сил поля на перенесение заряда qx из бесконечности в точку, где потенциал равен Либо эта работа равна что в формуле (2) величина в скобках равна удвоенной энергии взаимодействия.
Пользуясь формулой (2), рассчитываем энергию взаимодействия диполя с внешним полем. Эта энергия равна (рис. 2).

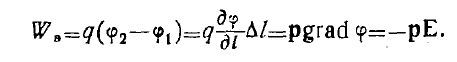(3)

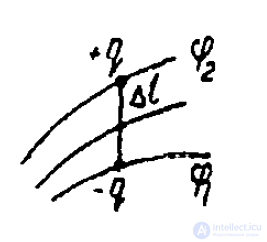
Рис. 2
Знак «—» означает, что энергия взаимодействия, или иначе — потенциальная энергия диполя, наибольшая, когда момент диполя р противоположно направлен вектору Е и, наоборот, когда вектор р совпадает по направлению с вектором Е, потенциальная энергия диполя в электрическом поле наименьшая.
энергия электростатического поля при непрерывном распределении зарядов с плотностьюр, как следует из формулы (1), равна

2. Энергия электростатического поля в анизотропной среде.

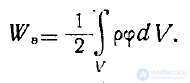
Симметричность тензора диэлектрической проницаемости Согласно формуле (3) работа, затраченная полем на поляризацию диэлектрика единицы объема при создании вектора поляризации
dP, равна
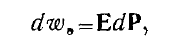, (4)
причем в случае анизотропной среды

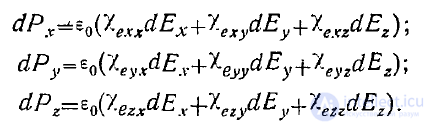
Иначе говоря, выражение (4) представляет собой работу, затрачиваемую на изменение составляющих поля от 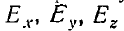соответственно до .

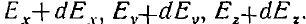Если составляющие поля принимают первоначальное значение Ех, Еу, Е2, то согласно закону сохранения энергии изменение энергии поля должно равняться той же величине (4). Следовательно, величина 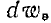из (4) должна являться полным дифференциалом функции .

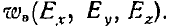Отсюда следует, что должно быть

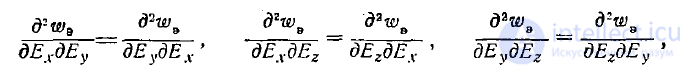(5)

тo есть смешанные производные от каких-либо двух аргументов функции \Ѵа не должны зависеть от порядка дифференцирования.

Следствием этого требования является симметричность тензора Электрической восприимчивости и соответственно симметричность тензора диэлектрической проницаемости.

Проиллюстрируем этот вывод, для упрощения предполагая, что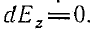

Имеем:

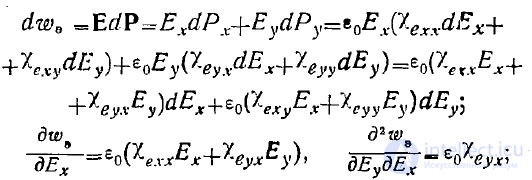
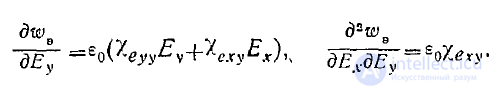
Отсюда видно, что, действительно, выполнение условий (5) требует выполнения равенств

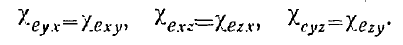
Симметричность тензора электрической восприимчивости влечет за собой симметричность тензора диэлектрической проницаемости, поскольку

Эллипсоид энергии тензора диэлектрической проницаемости (эллипсоид Френеля)

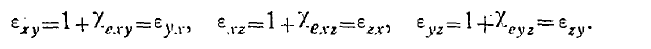
Энергия электростатического поля в анизотропной среде в единице объема, учитывая симметричность тензора диэлектрической проницаемости, может быть представлена в виде

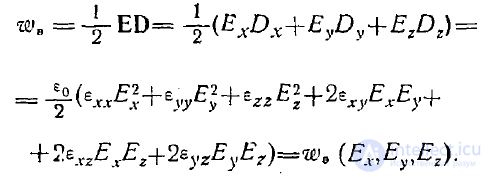(6)

Из этого выражения видно, что уравнение

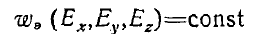
представляет собой уравнение поверхности эллипсоида в пространстве, координатами точек которого являются составляющие вектора
напряженности поля Е r , Ev, E'z (рис. 3 ) . Этот эллипсоид назывеется эллипсоидом тензора диэлектрической проницаемости или эллипсоидом Френеля.

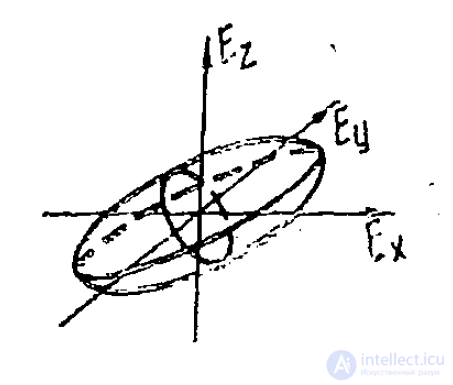
Рис. 3
Из аналитической геометрии известно, что уравнение эллипсоида принимает наиболее простой вид в прямоугольной системе координат, оси которого совпадают с осями эллипсоида.

Точно так же, по аналогии нетрудно видеть, что существует прямоугольная система координат в пространстве Е ѵ, Еу, Ег, в которой уравнение эллипсоида принимает вид (рис. 4),

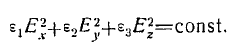(7)

Величины 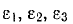называются главными значениями тензора диэлектрической проницаемости, а направления осей называются главными направлениями тензора диэлектрической проницаемости.
Физический смысл главных значений H главных направлений тензора диэлектрической проницаемости состоит в том, что если направить вектор Ъ по какому-либо из главных направлений, причем оси координат совпадают с последними, то вектор D оказывается коллинеарным с Е, т. е.

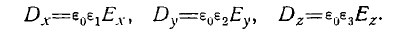(8)

Главные направления анизотропной среды, например кристалла, определяются структурой кристалла. Согласно изложенному в кристалле имеются три главных направления и эти направления взаимно перпендикулярны.
Если в какой-то фиксированной точке кристалла менять направление и величину вектора Е таким образом, чтобы конец его в соответствии с формулой (7) описывал поверхность эллипсоида, то при этом энергия электростатического поля остается постоянной величиной. Разумеется, в качестве-составляющих поля Ех,Еу Ez должны быть взяты проекции вектора Е па направление главных осей кристалла.

Главные значения тензора диэлектрической проницаемости можно определить исходя из следующих соображений.
По математическому смыслу тензор диэлектрическрй проницаемости преобразует вектор Е в вектор D изменяя, вообще говоря, по-разному его составляющие.
Однако, как уже было сказано, существуют такие направления, что тензор диэлектрической проницаемости изменяет только величину вектора Е, не меняя его направления, в результате чего вектор
D оказывается коллпиеарным вектору Е.
' Поэтому если вектор Е направлен по какому-либо из главных направлений и его составляющие в некоторой системе координат Ех, Еу, Еz, то будем иметь:

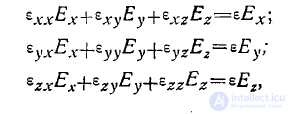
где s указывает, во сколько раз по величине изменяется вектор Е, будучи направленным по какому-либо из главных направлений тензора.
Эта система однородных уравнений относительно Ех, Еу, Еz имеет нетривиальное решение только тогда, когда ее определитель равен нулю, т. е.

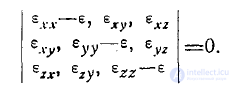
Этот определитель представляет собой кубическое уравнение относительно е. Поскольку тензор 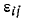симметричен, все три корня получаются вещественными.

Эти корни и суть главные значения тензора диэлектрической проницаемости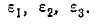

Исследование, описанное в статье про энергия электростатического поля, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое энергия электростатического поля и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория электромагнитного поля

Из статьи мы узнали кратко, но содержательно про энергия электростатического поля